Machine learning - decision tree

One 、 Decision tree

• Decision tree is a tree structure , Each internal node represents a test on an attribute , Each branch represents a test output , Each leaf node represents a category .
• Step by step from the root node to the leaf node .
• All the data will end up in the leaf node , It can be classified or regressed
  

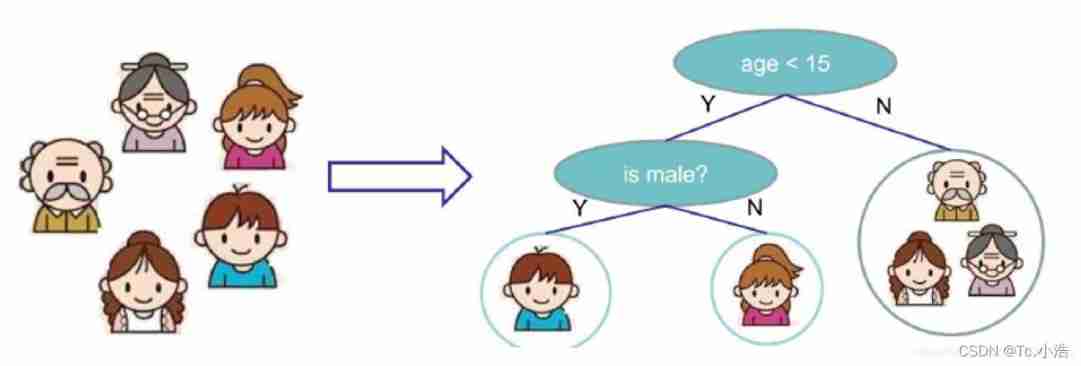
Think of a family as a piece of data , Enter into the decision tree , First, we will judge whether the age is greater than 15 year （ Artificially subjective value ）, If it is greater than 15, It is judged that it is less likely to play the game , Less than or equal to 15 At the age of, they think they are more likely to play games , Then subdivide it in the next step , Determine gender , If you are a boy, you think you are more likely to play games , If you are a girl, you are less likely to like playing games .

This is a simple decision tree process , It's kind of like the beginning python The progress of learning if-else The procedure for classifying grades of good and bad grades . however , The order of classification in the decision tree is usually not interchangeable , For example, why should we put the judgment of age before the judgment of gender , It is because we hope that the first decision and judgment can realize the screening of most data , Do everything you can right , Then proceed to the next step , Then realize the fine adjustment of the deviation data in the previous step , Therefore, the importance of the root node can be imagined , It should realize the rough judgment of data samples , Filter out more accurate data . You can compare basketball games , Of course, first in the starting lineup , Second, I'm considering substitutes , Supplement the short board .

So here's the problem ？（ How to select the root node ）—— Why should we divide by age first , Or what makes you think they're starting ？

What is the basis of judgment ？？？ The next? ？ How to segment the secondary root node ？？？

Training and testing of decision tree

• Training phase ： Construct a tree from a given training set （ Select features from nodes , How to segment features ）
• Testing phase ： According to the constructed mathematical model, just make a series from top to bottom
• Once the decision tree is constructed , So the task of classification or prediction is very simple , It only needs one time , So the difficulty is how to construct a tree ？

Two 、 Entropy function

The goal is ： Pass a measure , To calculate the classification situation after branch selection through different features , Find the best one as the root node , And so on .

The measure - entropy ： Entropy is a measure of the uncertainty of a random variable （ explain ： Speaking human is the degree of chaos inside an object , For example, there is everything in the voluntary grocery market. It must be chaotic , If only one brand is sold in the exclusive store, it will be much more stable ）

for instance ： as follows ,A After the decision classification is completed, there are three triangles and two circles on one side , The other side is a triangle , and B After the decision classification, one side is triangle and the other side is circle , Obviously B The decision-making judgment of the scheme is more reliable , Using entropy to explain is that the smaller the entropy （ The lower the level of confusion ）, The more effective the decision is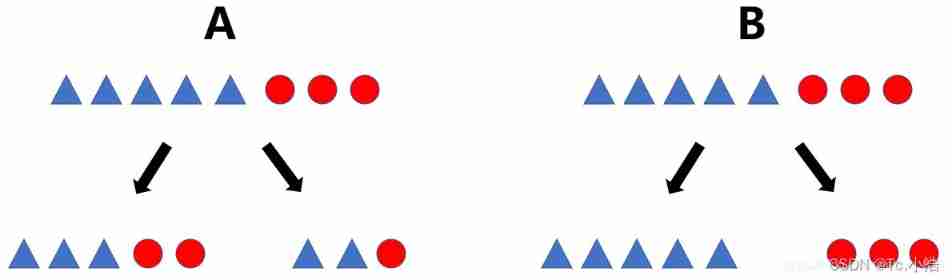

The formula ：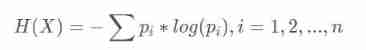

Here, the above example is used to interpret the formula , Just look at the classification results on the left , about B Medium , Only the triangle , That is, a classification result ,$p_i$
Is the value probability , It's here for 100%, Let's combine log function , Its value is [0,1] Between them is increasing , Then adding a minus sign in front is decreasing , So the B The calculation formula value brought in by the classification result on the right is 0, and 0 It's the lowest value in this formula again . Look again A The classification result on the left side of the middle , Because there are two situations , So there is accumulation in the formula , Calculate the entropy of the two results respectively , Finally, summarize , Its value must be greater than 0 Of , so A There are many categories in , Entropy is much larger ,B The categories in are relatively stable （ Then, when the classification task is heavy, do we want the entropy value of the data category to be large or small after branching through the node ？）

Not really , Before classification, the data has an entropy , After adopting the decision tree, there will also be entropy , Also take A give an example , The initial state is five triangles and three circles （ Corresponding to an entropy value 1）, After the decision, three triangles and two circles on the left are formed （ Corresponding entropy 2） And the two triangles on the right, a circle （ Corresponding entropy 3）, If the final entropy 2+ Entropy 3 < Entropy 1, Then we can judge that the classification is better , Better than before , That is, by comparing entropy （ uncertainty ） The degree of reduction determines whether the decision is good or bad , It doesn't just look at the size of entropy after classification , It depends on the change of entropy before and after decision-making .

3、 ... and 、 Decision tree construction example

Here we use the sample data provided on the official website to explain , The data is 14 Days of playing （ The actual situation ）; Characterized by 4 Kinds of environmental changes （$x_i$ ）; The final goal is to build a decision tree to predict whether to play or not （yes|no）, The data are as follows

$x_1$: outlook
x2 : temperature
x3 : humidity
x4: windy

play: yes|no

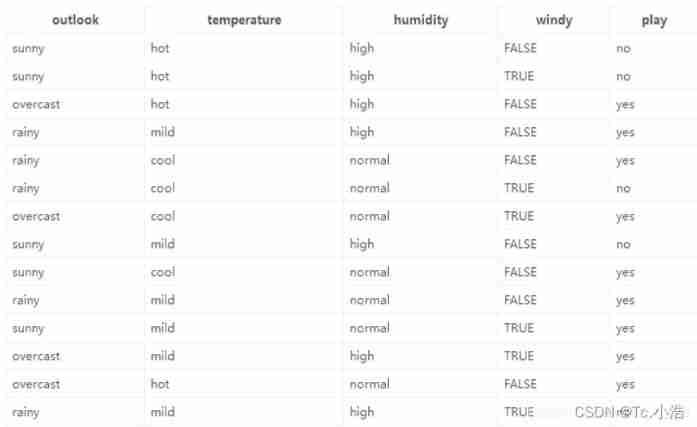
According to the data, there are 4 Species characteristics , Therefore, when building the decision tree, the choice of root node has 4 In this case , as follows . So back to the original question , Which is the root node ？ whether 4 All kinds of division methods are OK ？ therefore Information gain It's about to make a formal appearance

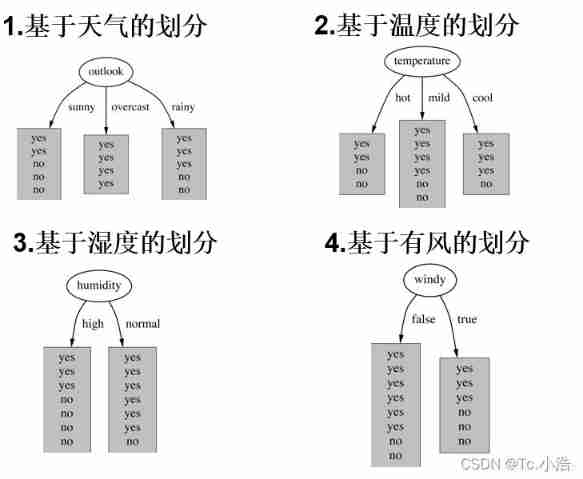
Because it is to judge the change of entropy before and after decision-making , First, make sure that in the historical data （14 God ） Yes 9 Heaven plays ,5 God doesn't play , So the entropy at this point should be （ commonly log The bottom of the function 2, It is required to unify the base number when calculating ）：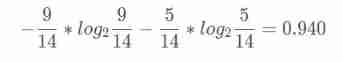

Start with the first feature , Calculate the change of entropy after decision tree classification , Or use the formula to calculate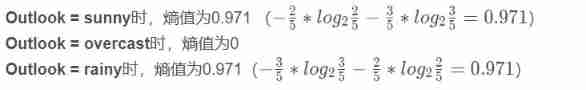

Be careful ： Directly compare the calculated result with the initial result calculated above ？ （ Of course not. ,outlook Fetch sunny,overcast,rainy There are different probabilities , Therefore, the final calculation results should consider this situation ）

The final entropy calculation is ：14 In the day 5 God sunny,4 God overcast,5 God rainy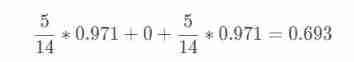

Information gain ： The entropy of the system changes from the original 0.940 Down to 0.693, The gain is
gain(outlook)=0.247

By analogy , The information gains of the remaining three feature classifications can be calculated as follows ：
$
gain(temperature)=0.029,gain(humidity)=0.152,gain(windy)=0.048$
Finally, we can choose the biggest one , So I went through the features , Found the root node （ The eldest brother ）, Then continue to find child nodes through information gain in the rest （ The second ）…, Finally, the whole decision tree is built ！

Four 、 Information gain rate and gini coefficient

Before, we used information gain to judge whether there is any problem with the root node , Or whether this method exists bug, Some problems cannot be solved ？？？ The answer is of course , For example, use the one above 14 Personal playing data , Add a feature here, which is the number of times you play ID, Respectively 1,2,3,…,12,13,14, Then if the decision is made according to this feature , as follows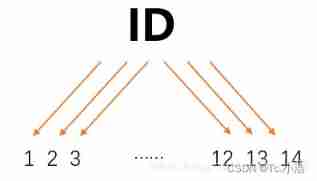

The results of decision-making and judgment based on this feature can be found to be a single branch , The result of calculating entropy is 0, The result information gain of this classification is the largest , It shows that this feature is very useful , If you still judge by information gain , The tree model will follow ID Select the root node , In fact, it is not feasible to make decisions and judgments in this way , Just watch every time you play ID I can't say whether I can play on this day .

From the above example, it can be found that information gain cannot solve this feature classification （ similar ID） There are many cases with special results , Therefore, another decision tree algorithm called Information gain rate and gini coefficient

Here is an introduction to the algorithm used in building the decision tree （ As for the previous English address , Just know that it is a referential relationship , For example, information gain can also be used ID3 To said ）：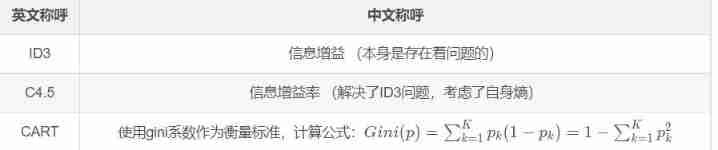

gini The coefficient calculation formula is similar to the measurement standard of entropy , But the calculation method is different , The smaller the value here, the better the effect of this decision classification , For example, when p The cumulative value of is taken as 1 了 , Then the final result is 0, When p When the value is small , After squared, it's smaller , The result of this calculation is close to 1 了

Information gain rate It is an improvement of the method of Judging according to entropy , and gini coefficient Is to start a new stove , Has its own calculation method

5、 ... and 、 Decision tree pruning strategy

Why pruning ： Decision tree over fitting is risky , In theory, data can be completely separated
pruning strategy ： pre-pruning , After pruning
pre-pruning ： At the same time, the decision tree is established and the pruning operation is carried out
After pruning ： When the decision tree is established, pruning operation is carried out later

Pre pruning method ： Limit depth （ For example, after specifying a specific value, it will not be split ）、 Number of leaf nodes 、 Number of leaf node samples 、 Information gain, etc
Back pruning method ： By a certain measure ,$C\alpha (T)=C(T)+\alpha \ast \mid T_{leaf}|$, More leaf nodes , The greater the loss

Post pruning workflow , For example, select the following nodes , Judge whether it will not split ？ The condition of not splitting is that the result after splitting is worse than that before splitting .

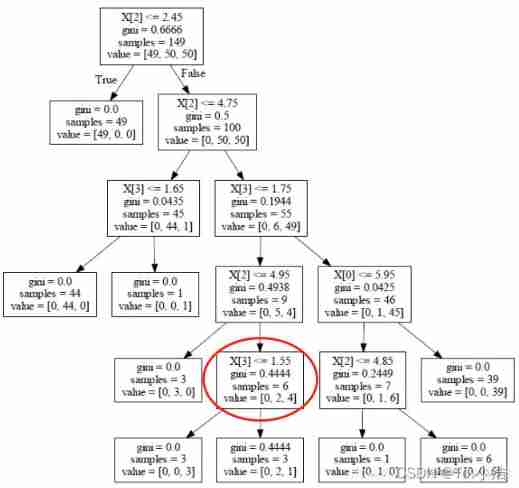
According to the above calculation formula , Before splitting
$C_{\alpha }(T)=0.4444\ast 6+1\ast \alpha$
After splitting, the sum of the two leaf nodes is added
$C_{\alpha }(T)=3\ast 0+1\ast \alpha +0.4444\ast 3+1\ast \alpha =0.444\ast 3+2\ast \alpha$
Finally, it becomes comparing the two values , The greater the value, the greater the loss , The worse , The size of the value depends on our given α value ,α The greater the value given , The more the model controls over fitting , When the value is small, we want the model to achieve better results , But fitting is not very important

6、 ... and 、 classification 、 Return to the task

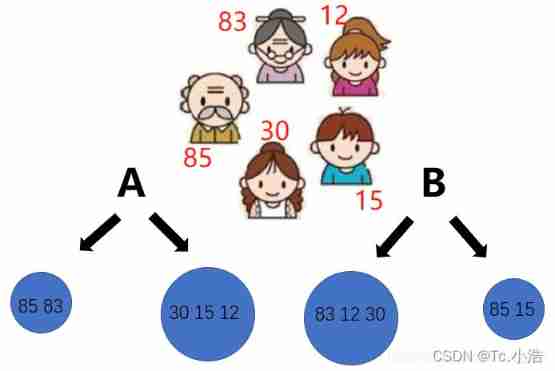
The tree model does the classification task , What determines the type in a leaf node ？ Also use the original illustration as an example , Tree model belongs to supervised algorithm , The data is already labeled before input , For example, below “-” For not playing games .“+” Represents playing games , Then there are three classification results in the red box on the right “-” The data of , The modes of the data are classified as “-”, So if there is data in this category later , Will be marked as “-”, Therefore, the classification task is determined by the mode of the data in the leaf node , The minority is subordinate to the majority , There are... In a leaf node 10 individual “-”,2 individual “+”, Then the leaf node is classified as “-”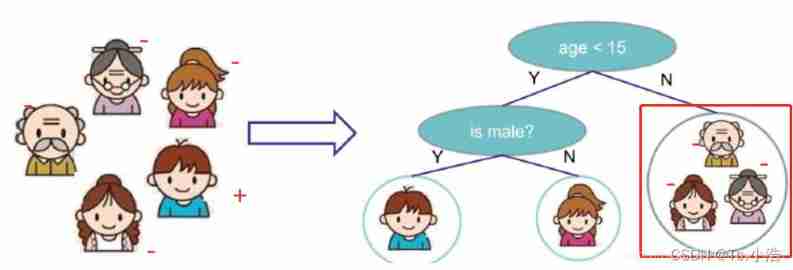

The approach of regression task and classification task is almost the same , But the way of evaluation is different , Regression is measured by variance , For example, judge the above five people according to their age , Whether it is the elderly , In fact A programme , Obviously, its variance is less than B Variance in the scheme , That is, man-made A The division method in the scheme is more reasonable . Since the problem of data regression cannot be avoided , The numerical calculation method in the leaf node is the average of each data , Then, when using the tree model for prediction , If the data falls into the leaf node, the value is the average value calculated before , If so A The right leaf node in the scheme , The predicted result is (30+15+12) /3 =19

Reference resources ：https://blog.csdn.net/lys_828/article/details/108669442