Comparison of usage scenarios and implementations of extensions, equal, and like in TS type Gymnastics

TS Type gymnastics And extends,Equal,Alike Use scenario and implementation comparison

In the program , Judging equality is a very important content , stay TS Equal in judgment （ In fact, it belongs to xxx Range ） It's using extends. Only extends Nature is not enough , So there are many tool classes that have some very subtle skills to implement Strictly equal The function of

Next, we will talk about several tool classes Equal and Alike. this 2 It's not TS The official realization of , And in TS The tools encapsulated by the great God in the warehouse of gymnastics practice

extends The role of

Let's review extends And most application scenarios

//  - 1
type ID = string | number
type TestID = ID extends string ? true : false  // false
type TestID2 = string extends ID ? true : false // true


//  - 2
type UnionType = string | number | boolean
type testUnion = string extends UnionType ? true : false // true
type testUnion2 = [string] extends [UnionType] ? true : false // true
type testUnion3 = [UnionType] extends [string] ? true : false // false

above 2 In one case

ID yes string/number type , therefore ID The range of values is ratio string The range of types is large ,TestID The return value is naturally false 了

And one string type , yes stay string|number Within the scope of , So naturally true 了

The same is true for others in the array

Understand the principle of the above example , That's it This question

use extends The characteristics of the solution 01097-medium-isunion

extends It is a judge with its own range judgment , As long as it is within the scope of another type , It will be judged as true

01097-medium-isunion The demand of the topic ： Determine whether an incoming type union type

What is? union（ union ） Type? , It consists of multiple types union And become , among | Just for Glue multiple types

The test cases are as follows ： Very representative

type cases = [
  Expect<Equal<IsUnion<string>, false >>,
  Expect<Equal<IsUnion<string|number>, true >>,
  Expect<Equal<IsUnion<'a'|'b'|'c'|'d'>, true >>,
  Expect<Equal<IsUnion<undefined|null|void|''>, true >>,
  Expect<Equal<IsUnion<{ a: string }|{ a: number }>, true >>,
  Expect<Equal<IsUnion<{ a: string|number }>, false >>,
  Expect<Equal<IsUnion<[string|number]>, false >>,
  // Cases where T resolves to a non-union type.
  Expect<Equal<IsUnion<string|never>, false >>,
  Expect<Equal<IsUnion<string|unknown>, false >>,
  Expect<Equal<IsUnion<string|any>, false >>,
  Expect<Equal<IsUnion<string|'a'>, false >>,
]

According to the above extends Introduction to , We can use the following principles to solve this problem

• string extends string | number by true
• string | number extends string by false
• TS In gymnastics Union（ Joint type ） automatically “ deconstruction ”

The answer is as follows ：

type IsUnion<T,U = T> = T extends U ? U extends T ? false : true : false

stay IsUnion Inside ,T It's automatic “ deconstruction ”, Like What's coming in is string|number.

1. T It will automatically become string, And then U Compare
2. T It's becoming number , In the and U Compare
3. U Empathy become string and T（string/number） Compare

So it looks like T extends U Just a trinocular operator , In fact, they Already run 4 It's a comparison , Just one time for false, that extends The result is false

---

Don't believe it ？ Insert a digression to prove

Let's change the type to 'a' | 'b', This is also a union type , And then we put extends Replace them 2 Splices

type TestUnion<T extends string, U extends string = T> = `${T}-${U}`
type ResultUnio = TestUnion<'a' | 'b'>

// type ResultUnio = "a-a" | "a-b" | "b-a" | "b-b"

After seeing the results , You should be able to understand the above ,union The type will be automatically “ deconstruction ” It means ,T Will be automatically deconstructed to a and b,U It will also be automatically deconstructed into a and b, Then pair them in pairs ; The result is （ What I don't understand is pondering ）

Can understand this demo after , There are several questions that will use this knowledge point , Circle to test

End of digression

---

Back to a few examples of test cases

• { a: string|number } and [string|number] It's not a union type , Because they all belong to the same object , their Attribute values are union types , And they themselves are not

• The last thing left 4 Of the test cases , such as string|never , string|'a' It also does not meet Union of multiple types The meaning of

  • never Note that no type matches , It's like whether sterilized kittens and normal kittens can give birth to new kittens ？ No way . So they Cannot unite
  • as for string|'a' ‘a’ It belongs to string Type of , It's like A male kitten and a male black kitten , They can union Do you ？ They all belong to Male cat , Only union , The union cannot produce results
  • therefore string|any Same as above ,any Everything , Nothing can be compared with any Form a union

however ！ Although they cannot form a joint type , But this will not report an error , Like this Take off your pants and fart
TS It will automatically help them choose a type with a large range as the joint result

like A male kitten and a male black kitten , They are collectively called Male cat

type StringUnion = string | 'a' //  The result is  string
type StringUnion2 = string | any //  The result is  any

Use tips to achieve Equal Congruent judgment

Want to say Equal Usage scenarios of ,TS Every exercise question of type gymnastics is used

I was in This question was particularly noticed

type User = {
    
  name?: string
  age: number
  address: string
}

type User2 = {
    
  name?: string
} & {
    
  age: number
  address: string
}

type R = Equal<User1, User2> // false
type R2 = User1 extends User2 ? (User2 extends User1 ? true : false) : false // true

Look at the above. demo, If only extends To judge , They are equal （U1 == U2 && U2 == U1）
But there are differences in writing ,User2 It is crossed by cross type
That's why extends The reason why we can't do exactly the same

So there it is Equal The plan , have a look Equal The implementation of the

export type Equal<X, Y> =
  (<T>() => T extends X ? 1 : 2) extends
  (<T>() => T extends Y ? 1 : 2) ? true : false

At first, I thought for a long time

• T It came out there ？
• T As a generic , Pass into a function , Then come back ？
• T Why is it equal to X ？
• T Why is it equal to Y 了 ？

Finally, I see the answer here , A little feeling How does the Equals work in typescript?

According to the principle of looking at brackets first hold Equal The equation of is divided into 3 From the content of this paragraph

• (<T>() => T extends X ? 1 : 2) Assuming that 1 type
• (<T>() => T extends Y ? 1 : 2) Assuming that 2 type

All in all : 1 type extends 2 type ? true : false

and <T>() How do you understand that ？ There is a very important sentence ( Also from stackoverflow Answers on )

The assignability rule for conditional types <…> requires that the types after extends be “identical” as that is defined by the checkerF

Corresponding translation ： Condition type <…> The allocability rule of requires the extended type and the type defined by the inspector “ identical ”

According to the above 1 type ,2 type To a demo Understanding ：

declare let x: <T>() => T extends number ? 1 : 2
declare let y: <T>() => T extends number ? 1 : 2
declare let z: <T>() => T extends string ? 1 : 2

var str: string = '1'
str = 2 //  Report errors 

x = 100 //  Report errors 
x = y
x = z //  Report errors 
y = z //  Report errors 

• 2 Assign a value to str When an error Type ‘number’ is not assignable to type ‘string’.
• x The assignment is 100 When an error Type ‘number’ is not assignable to type ‘<T>() => T extends number ? 1 : 2’.

Watch this carefully 2 Error messages , They all belong to ts(2322) Wrong number . Then it can be understood as <T>() => T extends number ? 1 : 2 Actually and string equally , It's a Single type , Not what we think function

• y Assign a value to x Nothing

• z Assign a value to x and z Assign a value to y Will prompt the following error

Type '<T>() => T extends string ? 1 : 2' is not assignable to type '\<T\>() => T extends number ? 1 : 2'.
  Type 'T extends string ? 1 : 2' is not assignable to type 'T extends number ? 1 : 2'.
    Type '1 | 2' is not assignable to type 'T extends number ? 1 : 2'.
      Type '1' is not assignable to type 'T extends number ? 1 : 2'.

To put it bluntly, there are different types Can't assign a value , because The allocability rule requires the extended type and the type defined by the inspector “ identical ”

See here , Is it possible to understand ？1 type and 2 In fact, the final form is just an exaggerated one type . And then the little tail (1 and 2, It's really to make up the number of words , in order to extends It's used for rounding up the number of words )

For example, change it a little , The equations are all wrong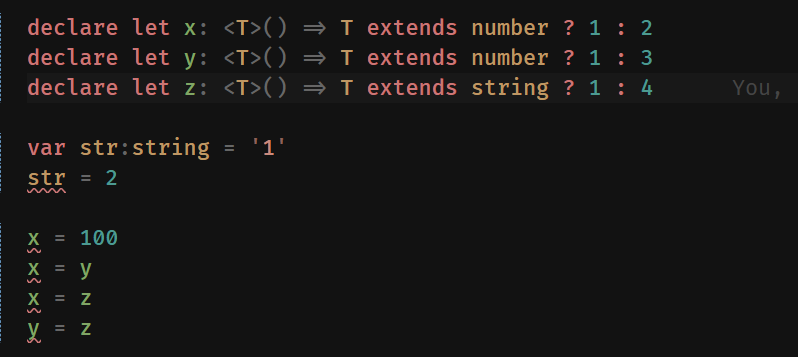

Change the definition of generics , It won't report an error

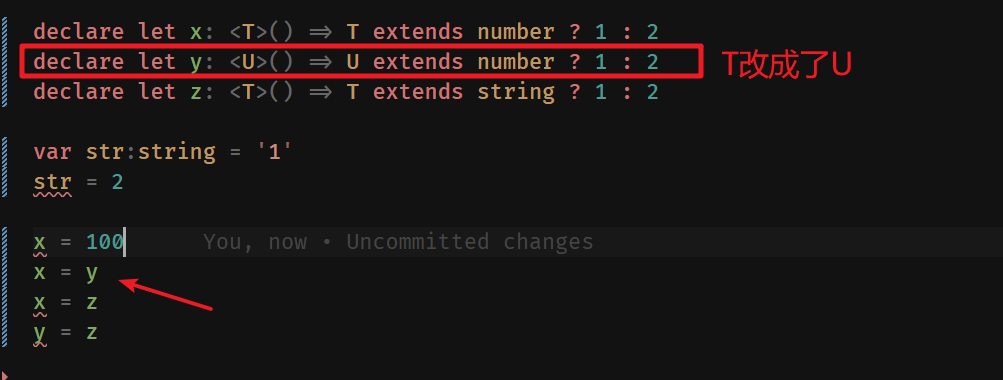
To sum up, it's the same sentence

Condition type <…> The allocability rule of requires the extended type and the type defined by the inspector “ identical ”

I understand demo And parsed text , So understand Equal Not to mention , as long as 1 The type and 2 type extends, Based on the above “ identical ” characteristic , That's all waiting

and Equal Much like the Alike

Alike and Equal The same is to judge equality , In the previous article 《TS Type gymnastics And Key value judgment in the loop ,as Keyword use 》 It's said in The test case of is used Alike

type User = {
    
  name?: string
  age: number
  address: string
}

type User2 = {
    
  name?: string
} & {
    
  age: number
  address: string
}

//  hold  Equal  Switch to  Alike  What you get is  true  Result 
type R = Alike<User1, User2> // true
type R2 = User1 extends User2 ? (User2 extends User1 ? true : false) : false // true

If you use Alike, So just now Equal by false Of 2 An object can be changed into true 了

Alike It cannot be simply understood as T extends U && U extends The implementation of the , Absolutely not

• Alike The implementation is as follows ：

export type MergeInsertions<T> = T extends object ? {
     [K in keyof T]: MergeInsertions<T[K]> } : T

export type Alike<X, Y> = Equal<MergeInsertions<X>, MergeInsertions<Y>>

Used MergeInsertions Tool class of , The function of this is the same as yesterday type Clone<T> = Pick<T, keyof T> almost ！ Just say mine Pick Can only Pick First floor , and MergeInsertions It takes into account the multi-layer nesting of objects （ Upgraded version Clone, It means a little shallow copy and deep copy ）

{} & {} after MergeInsertions After processing , It will also be merged into an object {}, Then take it Equal contrast . Have to say , That's wonderful

above-mentioned Alike It cannot be simply understood as T extends U && U extends The implementation of the

Look at a case ：

type TestUnion = {
     a: string } | {
     a: number }

type IsLike = Alike<TestUnion, TestUnion> // true
type IsUnionResult = IsUnion<TestUnion> // true

type IsLike2 = Alike<string, string> // true
type IsUnionResult2 = IsUnion<string, string> // false

For a single type ,T extends U && U extends Can determine whether Union , and Alike We can only judge whether they are equal

So if you want to judge IsUnion We have to rely on double extends,Alike Just a loose equality operator

summary

• extends It's a Comparison of subsets , as long as x yes y Subset , that x extends y for true
• Determine whether a type is union type , It also uses extends A subset of Characteristics
  • If x yes y Subset , that y It can't be x Subset
  • x extend y also y also extends x Words , It can only be said that they are A single The type of , There is no union
• Equal The function is cleverly used TS A feature of
  • The assignability rule for conditional types <...> requires that the types after extends be "identical" as that is defined by the checkerF
  • Through a similar Formula substitution Scene judgment 2 Are the types Congruence
  • Single type and Cross type Incongruence
• If you want to relax the conditions , Just want to judge 2 If all fields of a type are the same, they are equal
  • Just use Alike ,Alike It uses a MergeInsertions(Clone Upgraded version ) To merge cross types into Single type
  • With a single type , You can use it Equal To compare
  • For a single type ,T extends U && U extends Can determine whether Union , and Alike We can only judge whether they are equal （ So don't confuse Alike and IsUnion Implementation principle of ）

Whether it's IsUnion Implementation principle of , still Alike Loose grammar contrast ,Equal Strict congruence of ,extends Range subset judgment ; All have their own use scenarios , Do questions everyday / Development should Look at the scheme below