Comics: looking for the best time to buy and sell stocks

Want to make APP Same thing as WeChat , Can run small programs smoothly ？ | Experience will send you to Xinjiang 、 Huawei 、 Cherry keyboard ！>>>

Some time ago , Xiaohui released the next two on the stock trading algorithm problem explanation , It has inspired a lot of interest from small partners .

This time, , Xiao Hui integrates these two comics together , And fixed some of the details of the error , Thank you for your advice .

—————  the second day   —————

What does that mean ？ Let's take an example , Given the following array ：

The corresponding stock up and down curve of this array is as follows ：

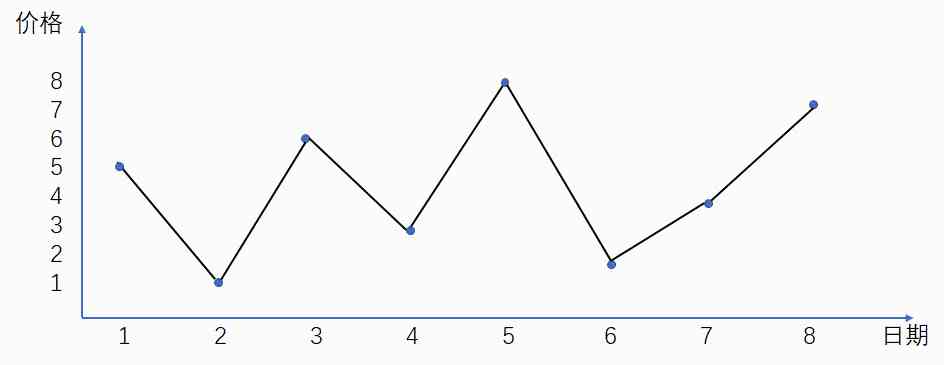
obviously , From 2 The price is 1 Buy when , From 5 The price is 8 Sell when , You can get the most out of it ：

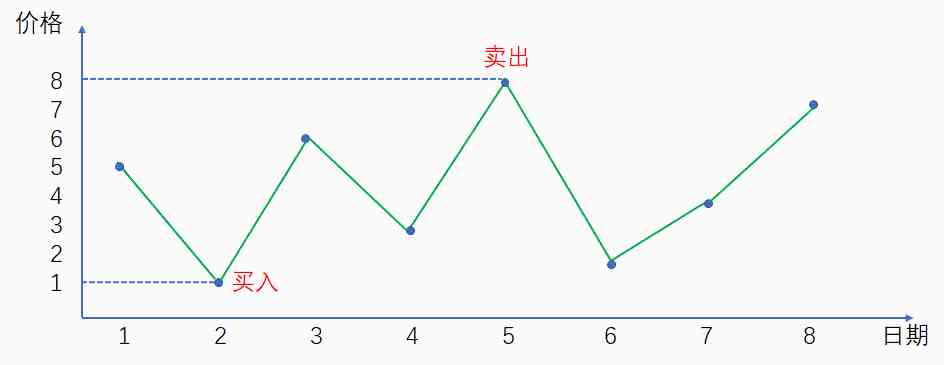
The biggest payoff at this point is 8-1=7.

In the example above , Maximum 9 At the minimum 1 In front of , How can we trade ？ We can't turn back time ？

————————————

The following is an example , If we have set the price 4 It's time to sell , So which is the best time to buy ？

We have to choose the price 4 The previous interval , And must be the minimum value in the interval , obviously , The best choice is price 2 The timing of the .

The first 1 Step , Initialization operation , Put the first 1 Elements as temporary minimum price ; The initial value of maximum return is 0：

The first 2 Step , Traverse to the 2 Elements , because 2<9, So the current minimum price becomes 2; There is no need to calculate the difference （ Because the front element is bigger than it ）, The biggest benefit is still 0：

The first 3 Step , Traverse to the 3 Elements , because 7>2, So the current minimum price is still 2; As we said just now , Suppose the price 7 For selling point , The best buy point for that is the price 2, The difference between the two 7-2=5,5>0, So the biggest payoff right now is 5：

The first 4 Step , Traverse to the 4 Elements , because 4>2, So the current minimum price is still 2;4-2=2,2<5, So the biggest payoff is still 5：

The first 5 Step , Traverse to the 5 Elements , because 3>2, So the current minimum price is still 2;3-2=1,1<5, So the biggest payoff is still 5：

And so on , We walk through the end of the array , The minimum price at this time is 1; The biggest benefit is 8-1=7：

public class StockProfit {

    public static int maxProfitFor1Time(int prices[]) {
        if(prices==null || prices.length==0) {
            return 0;
        }
        int minPrice = prices[0];
        int maxProfit = 0;
        for (int i = 1; i < prices.length; i++) {
            if (prices[i] < minPrice) {
                minPrice = prices[i];
            } else if(prices[i] - minPrice > maxProfit){
                maxProfit = prices[i] - minPrice;
            }
        }
        return maxProfit;
    }

    public static void main(String[] args) {
        int[] prices = {9,2,7,4,3,1,8,4};
        System.out.println(maxProfitFor1Time(prices));
    }

}

Let's take the array in the following figure for example , Take a visual look at the timing of buying and selling ：

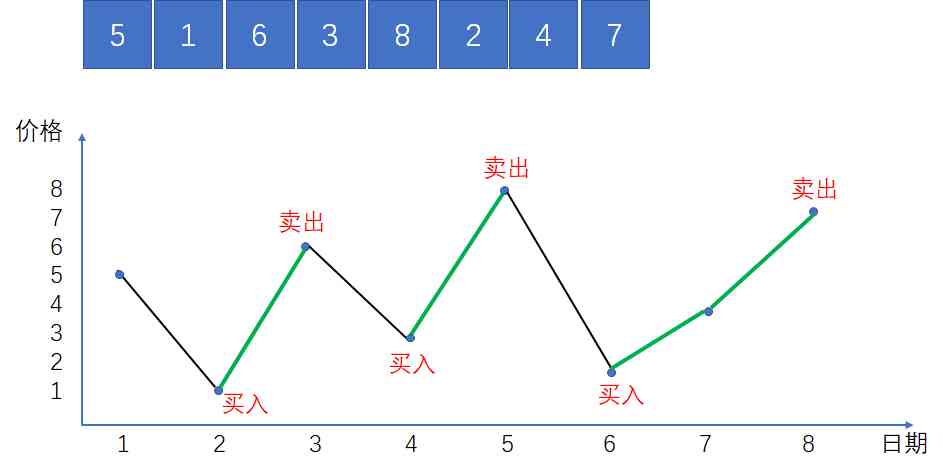
In the picture , The green line represents the stage of price rise . Since there is no limit to the number of transactions , So we can buy at every low point , Sell at every high .

thus , All the green parts are our gains , The maximum total return is the sum of these local returns ：

（6-1）+（8-3）+（4-2）+（7-4） = 15

As for how to judge these green rising stages ？ It's simple , We traverse the entire array , But where the latter is greater than the former , It means that the stock price is in the rising stage .

    public int maxProfitForAnyTime(int[] prices) {
        int maxProfit = 0;
        for (int i = 1; i < prices.length; i++) {
            if (prices[i] > prices[i-1])
                maxProfit += prices[i] - prices[i-1];
        }
        return maxProfit;
    }

Let's still take the previous array as an example ：

First , Look for 1 The best buy and sell point under the sub limit ：

It's impossible to cross the two positions , So we found number one 1 After the second trading position , Take out this pair of buy and sell points and the elements in between ：

Next , We follow the same line of thinking , And then look for the rest of the elements 2 The best buy and sell point for sub - Sales ：

thus , We found the most 2 The best choice in the case of sub sales ：

For the array above , If we solve it twice independently , The best buy and sell points are 【1,9】 and 【6,7】, The biggest benefit is  （9-1）+（7-6）=9：

But actually , If you choose 【1,8】 and 【3,9】, The biggest benefit is （8-1）+（9-3）=13>9：

When the first 1 The next best buy and sell point is determined , The first 2 What kind of situation will there be in the position of buying and selling points ？

situation 1： The first 2 Second best buy and sell point , In the 1 Buy sell left

situation 2： The first 2 Second best buy and sell point , In the 1 On the right side of the buying and selling point

situation 3： The first 1 The buy and sell range is cut off from the middle , Split it back into two deals

that , How to judge what kind of situation a given stock price array belongs to ？ It's simple , In the 1 After the next maximum buying and selling point is determined , We can compare which situation brings about the largest increase in revenue ：

Looking for the biggest gains on the left and right is easy to understand , What's the use of looking for the biggest drop in the middle ？

Think about it and you'll know , When the first 1 When the sale needs to be split up , The biggest drop in the trading range , It's the same as the profit increment after the split （ Similar to the bottom of the stock market operation ）：

thus , We can sum up the following formula ：

Maximum total revenue = The first 1 The second largest return + Max（ The biggest gain on the left , The biggest drop in the middle , The biggest gain on the right ）

So called dynamic programming , It is to simplify a complex problem into smaller subproblems , And then from the simple subproblem from the bottom up step by step recursion , Finally, we get the optimal solution of complex problems .

First , Let's analyze the current stock trading problem , This problem requires a certain number of days to be solved 、 The maximum return under a certain number of transactions .

Since the limit on the maximum trading of shares 2 Time , Then the stock transaction can be divided into 5 Stages ：

No business

The first 1 Buy... Times

The first 1 Time to sell

The first 2 Buy... Times

The first 2 Time to sell

We set the trading stage of a stock as a variable m（ Use from 0 To 4 The value of represents ）, Set the range of days as a variable n. And the biggest benefit of our solution is , Influenced by these two variables , It can be expressed as follows ：

The biggest gain = F（n,m）（n>=1,0<=m<=4）

Since functions and variables have been determined , Next, we're going to identify two elements of dynamic planning ：

1. The initial state of the problem
2. The state transition equation of the problem

What is the initial state of the problem ？ We assume that the range of trading days is limited to 1 God , That is to say n=1 The situation of ：

1. If there is no business , That is to say m=0 when , The biggest benefit is obviously 0, That is to say  F（1,0）= 0

2. If there is 1 Buy... Times , That is to say m=1 when , It's equivalent to subtracting the first one out of thin air 1 Day's share price , The biggest profit is negative day stock price , That is to say  F（1,1）= -price[0]

3. If there is 1 Time to buy , That is to say m=2 when , The sale offsets （ Of course , It doesn't make sense ）, The biggest benefit is 0, That is to say  F（1,2）= 0

4. If there is 2 Buy... Times , That is to say m=3 when , Same as m=1 The situation of ,F（1,3）= -price[0]

5. If there is 2 Time to sell , That is to say m=4 when , Same as m=2 The situation of ,F（1,4）= 0

The initial state is determined , Let's take a look at the state shift . If the range of days is limited from n-1 Days increased to n God , So what happens to the maximum return ？

It depends on what stage is it now （ It's the number of buying and selling ）, And for the first time n Day stock price operation （ purchase 、 Sell or wait and see ）. Let's analyze the situation at each stage ：

1. If there was no sale before , And the first n The sky is still watching , So the biggest payoff is still 0, namely  F（n,0） = 0

2. If there was no sale before , And the first n Days to buy , So the biggest return is the negative day stock price , namely F（n,1）= -price[n-1]

3. If there was 1 Buy... Times , And the first n God chooses to wait and see , So the maximum profit is the same as before , namely  F（n,1）= F（n-1,1）

4. If there was 1 Buy... Times , And the first n Days to sell , So the biggest payoff is 1 The negative return on the second purchase plus the share price of the day , That is to say  F（n,2）= F（n-1,1）+ price[n-1]

5. If there was 1 Time to sell , And the first n God chooses to wait and see , So the maximum profit is the same as before , namely  F（n,2）= F（n-1,2）

6. If there was 1 Time to sell , And the first n Days go on 2 Buy... Times , So the biggest payoff is 1 The second sale income minus the share price of the day , namely F（n,3）= F（n-1,2） - price[n-1]

7. If there was 2 Buy... Times , And the first n God chooses to wait and see , So the maximum profit is the same as before , namely  F（n,3）= F（n-1,3）

8. If there was 2 Buy... Times , And the first n Days to sell , So the biggest payoff is 2 The second buy income minus the share price of the day , namely F（n,4）= F（n-1,3） + price[n-1]

9. If there was 2 Time to sell , And the first n God chooses to wait and see （ I can only wait and see ）, So the maximum profit is the same as before , namely  F（n,4）= F（n-1,4）

Last , We put the situation 【2,3】,【4,5】,【6、7】,【8,9】 Merge , It can be summed up as follows 5 An equation ：

F（n,0） = 0

F（n,1）=  max（-price[n-1],F（n-1,1））

F（n,2）=  max（F（n-1,1）+ price[n-1],F（n-1,2））

F（n,3）=  max（F（n-1,2）- price[n-1],F（n-1,3））

F（n,4）=  max（F（n-1,3）+ price[n-1],F（n-1,4））

From the back 4 In the equation , We can sum up the relationship between the maximum return of each stage and the previous stage ：

F（n,m） = max（F（n-1,m-1）+ price[n-1],F（n-1,m））

From this we can conclude that , The complete state transition equation is as follows ：

In the table , Different lines represent the maximum return under different day limits , The different columns represent the maximum returns at different stages of trading .

We still use the array from the previous example , Fill in the table on this basis ：

First , We fill in the initial state for the table ：

Next , We're starting to fill in the 2 Row data .

When there is no business , The maximum benefit must be 0, therefore F（2,0） The result is 0：

According to the previous state transition equation ,F（2,1）= max（F（1,0）-2,F（1,1））= max（-2,-1）= -1, So the first 2 Xing di 2 The result of the column is -1：

F（2,2）= max（F（1,1）+2,F（1,2））= max（1,0）= 1, So the first 2 Xing di 3 The result of the column is 1：

F（2,3）= max（F（1,2）-2,F（1,3））= max（-2,-1）= -1, So the first 2 Xing di 4 The result of the column is -1：

F（2,4）= max（F（1,3）+2,F（1,4））= max（1,0）= 1, So the first 2 Xing di 5 The result of the column is 1：

And then we go on with the state transition equation , Fill first 3 Row data ：

Next, fill in the 4 That's ok ：

And so on , We've been filling in the entire form ：

As shown in the figure , The last data in the table 13, It's the biggest benefit of the whole .

    // The maximum number of transactions 
    private static int MAX_DEAL_TIMES = 2;

    public static int maxProfitFor2Time(int[] prices) {
        if(prices==null || prices.length==0) {
            return 0;
        }
        // The maximum number of rows in a table 
        int n = prices.length;
        // The maximum number of columns in a table 
        int m = MAX_DEAL_TIMES*2+1;
        // Record data using a two-dimensional array 
        int[][] resultTable = new int[n][m];
        // Fill in the initial state 
        resultTable[0][1] = -prices[0];
        resultTable[0][3] = -prices[0];
        // Bottom up , Fill in the data 
        for(int i=1;i<n;++i) {
            for(int j=1;j<m;j++){
                if((j&1) == 1){
                    resultTable[i][j] = Math.max(resultTable[i-1][j], resultTable[i-1][j-1]-prices[i]);
                }else {
                    resultTable[i][j] = Math.max(resultTable[i-1][j], resultTable[i-1][j-1]+prices[i]);
                }
            }
        }
        // Return the final result 
        return resultTable[n-1][m-1];
    }

    // The maximum number of transactions 
    private static int MAX_DEAL_TIMES = 2;

    public static int maxProfitFor2TimeV2(int[] prices) {
        if(prices==null || prices.length==0) {
            return 0;
        }
        // The maximum number of rows in a table 
        int n = prices.length;
        // The maximum number of columns in a table 
        int m = MAX_DEAL_TIMES*2+1;
        // Record data using a one-dimensional array 
        int[] resultTable = new int[m];
        // Fill in the initial state 
        resultTable[1] = -prices[0];
        resultTable[3] = -prices[0];
        // Bottom up , Fill in the data 
        for(int i=1;i<n;++i) {
            for(int j=1;j<m;j++){
                if((j&1) == 1){
                    resultTable[j] = Math.max(resultTable[j], resultTable[j-1]-prices[i]);
                }else {
                    resultTable[j] = Math.max(resultTable[j], resultTable[j-1]+prices[i]);
                }
            }
        }
        // Return the final result 
        return resultTable[m-1];
    }

In this code ,resultTable From a two-dimensional array to a one-dimensional array . Because the maximum number of transactions is constant , So the spatial complexity of the algorithm also varies from O（n） Down to O（1）.

    public static int maxProfitForKTime(int[] prices, int k) {
        if(prices==null || prices.length==0 || k<=0) {
            return 0;
        }
        // The maximum number of rows in a table 
        int n = prices.length;
        // The maximum number of columns in a table 
        int m = k*2+1;
        // Record data using a one-dimensional array 
        int[] resultTable = new int[m];
        // Fill in the initial state 
        for(int i=1;i<m;i+=2) {
            resultTable[i] = -prices[0];
        }
        // Bottom up , Fill in the data 
        for(int i=1;i<n;i++) {
            for(int j=1;j<m;j++){
                if((j&1) == 1){
                    resultTable[j] = Math.max(resultTable[j], resultTable[j-1]-prices[i]);
                }else {
                    resultTable[j] = Math.max(resultTable[j], resultTable[j-1]+prices[i]);
                }
            }
        }
        // Return the final result 
        return resultTable[m-1];
    }

—————END—————

Friends who like this article , Welcome to the official account   Programmer Xiaohui , Watch more

 Order one [ Looking at ], It's the biggest support for Xiao Hui ！