Word2vec (skip gram and cbow) - pytorch

---

• Word vectors are vectors used to express the meaning of words , It can also be regarded as the feature vector of words . The technology of mapping words to real vectors is called word embedding .

One 、 Word embedding (Word2vec)

The unique heat vector cannot accurately express the similarity between different words ,word2vec The proposal of is to solve this problem , It maps each word to a fixed ⻓ The vector of degrees , These vectors can better express the similarity and analogy between different words .word2vec Contains two models ：Skip-Gram and CBOW, Their training depends on conditional probability . Because it is data without labels , therefore Skip-Gram and CBOW Are self-monitoring models .

1.Skip-Gram

Skip-Gram： The head word predicts the surrounding words

Every word has Two $d$ The vector representation of dimensions , Used to calculate conditional probability . The index in the dictionary is $i$ Any word of , Use them separately ${\mathbf{v}}_i\in {\mathbb{R}}^d$ and ${\mathbf{u}}_i\in {\mathbb{R}}^d$ Represents two vectors when it is used as a head word and a context word . Given the central word $w_c$（ The subscript indicates the index in the dictionary ）, Generate any contextual words $w_o$ The conditional probability of the vector dot product can be obtained by softmax Operation to model ：
$$P(w_o\mid w_c)=\frac{\text{exp}({\mathbf{u}}_o^{\top }{\mathbf{v}}_c)}{{\sum }_{i\in \mathcal{V}}\text{exp}({\mathbf{u}}_i^{\top }{\mathbf{v}}_c)}\text{\hspace{1em}(1)}$$
among , Thesaurus index set $\mathcal{V}=\{0,1,\dots ,|\mathcal{V}|-1\}$.

Given length is $T$ The text sequence of , Among them, the time step $t$ The word in place means $w^{(t)}$. It is assumed that the context word is generated independently given any central word . For context windows $m$,Skip-Gram The likelihood function of is the probability of generating all context words given any central word ：
$$\prod _{t=1}^T\prod _{-m\le j\le m,j\ne 0}P(w^{(t+j)}\mid w^{(t)})\text{\hspace{1em}(2)}$$

2.CBOW Model

CBOW： The surrounding words predict the central word

because CBOW There are multiple contextual words in , Therefore, when calculating the conditional probability, these context word vectors are averaged . For the index in the dictionary $i$ Any word of , Use them separately ${\mathbf{v}}_i\in {\mathbb{R}}^d$ and ${\mathbf{u}}_i\in {\mathbb{R}}^d$ Represents two vectors used as context words and head words （ Symbols and Skip-Gram On the contrary ）. Given the context word $w_{o_1},\dots ,w_{o_{2m}}$（ The index in the thesaurus is $o_1,\dots ,o_{2m}$） Generate any headword $w_c$ The conditional probability of is :

$$P(w_c\mid w_{o_1},\dots ,w_{o_{2m}})=\frac{\text{exp}\left(\frac{1}{2m}{\mathbf{u}}_c^{\top }({\mathbf{v}}_{o_1}+\dots ,+{\mathbf{v}}_{o_{2m}})\right)}{{\sum }_{i\in \mathcal{V}}\text{exp}\left(\frac{1}{2m}{\mathbf{u}}_i^{\top }({\mathbf{v}}_{o_1}+\dots ,+{\mathbf{v}}_{o_{2m}})\right)}\text{\hspace{1em}(3)}$$
Given length is $T$ The text sequence of , Among them, the time step $t$ The word in place means $w^{(t)}$. For context windows $m$,CBOW The likelihood function of is the probability of generating all the central words given their context words ：

$$\prod _{t=1}^{T}P(w^{(t)}\mid w^{(t-m)},\dots ,w^{(t-1)},w^{(t+1)},\dots ,w^{(t+m)})\text{\hspace{1em}(4)}$$

Two 、 Negative sampling and layering softmax

Skip-Gram The main idea is to use softmax Operation to calculate based on the given central word $w_c$ Generate upper and lower text $w_o$ Conditional probability of . because softmax The nature of the operation , Context words can be word lists $\mathcal{V}$ Any item in , The sum of items with the same size as the whole vocabulary . therefore , Skip-Gram Gradient calculation and CBOW All gradient calculations involve summation . But usually a dictionary has hundreds of thousands or millions of words , The computational cost of summing the gradient is huge ！

In order to reduce the computational complexity , Let's say Skip-Gram As an example, learn two approximate calculation methods ： Negative sampling and layered softmax.

1. Negative sampling

Given the central word $w_c$ Context window for , Any context word $w_o$ Events from this context window are considered to be probability modeled by ：

$$\begin{gathered} P(D=1\mid w_c,w_o)=\sigma ({\mathbf{u}}_o^{\top }{\mathbf{v}}_c) \\ =\frac{\exp ({\mathbf{u}}_o^{\top }{\mathbf{v}}_c)}{1+\exp ({\mathbf{u}}_o^{\top }{\mathbf{v}}_c)} \\ =\frac{1}{1+\exp (-{\mathbf{u}}_o^{\top }{\mathbf{v}}_c)}\text{\hspace{1em}(5)} \end{gathered}$$
Before negative sampling softmax( Many classification ), Now it is sigmoid( Two classification ).

Two classification , Multi classification can see the previous Logistic regression and multiple logistic regression This blog , The actual combat can be seen Logic returns to actual combat - Stock customer churn early warning model (Python Code ) This .

Maximize joint probability , Given length is $T$ The text sequence of , With $w^{(t)}$ Time step $t$ The word , The context window is $m$, Formula for ：

$$\prod _{t=1}^T\prod _{-m\le j\le m,j\ne 0}P(D=1\mid w^{(t)},w^{(t+j)})\text{\hspace{1em}(6)}$$
However , The formula 6 Consider only those events with positive samples . Only when all word vectors are equal to infinity , The joint probability is maximized to 1. Of course , Such a result is meaningless . In order to make the objective function more meaningful , Negative sampling adds negative samples sampled from a predefined distribution .

use $S$ Context words $w_o$ From the central word $w_c$ Context window events . For this involves $w_o$ Events , From predefined distribution $P(w)$ In the sample $K$ This is not from this context window Noise words . use $N_k$ Words indicating noise $w_k$（$k=1,\dots ,K$） Not from $w_c$ Context window events . Suppose positive and negative cases $S,N_1,\dots ,N_K$ These events are independent of each other . Negative sampling will be the original Skip-Gram The joint probability of （ The formula 2） rewrite , Change the conditional probability to the following formula ：
$$\begin{gathered} P(w^{(t+j)}\mid w^{(t)})\approx \\ P(D=1\mid w^{(t)},w^{(t+j)})\prod _{k=1,w_k\sim P(w)}^{K}P(D=0\mid w^{(t)},w_k) \end{gathered}$$
The loss function is negative log likelihood , Now the calculation cost of gradient is no longer related to the size of vocabulary , But with the number of noise words in negative sampling $K$( It's a super parameter ,$K$ The smaller the calculation cost, the lower ) of .

2. layered Softmax

layered Softmax Use a binary tree , Each leaf node of the tree represents a vocabulary $\mathcal{V}$ One of the words in .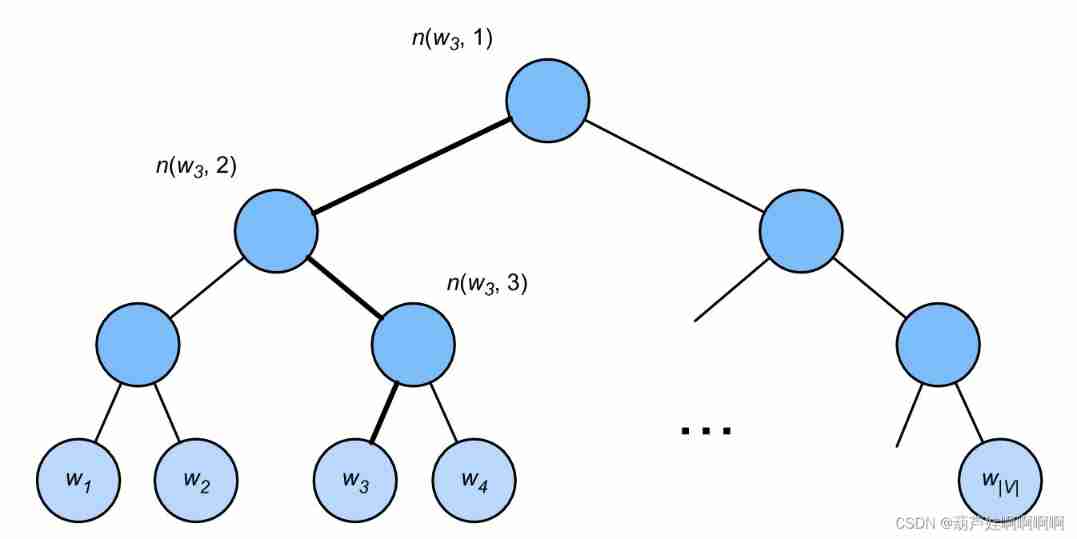

use $L(w)$ Represents the word in the binary tree $w$ The number of nodes on the path from the root node to the leaf node （ Including both ends ）. set up $n(w,j)$ For $j^{\mathrm{t}\mathrm{h}}$ node , The upper and lower text vectors are ${\mathbf{u}}_{n(w,j)}$.

for example ,$L(w_3)=4$. layered softmax The conditional probability is approximated as
$$P(w_o\mid w_c)\approx \prod _{j=1}^{L(w_o)-1}\sigma \left([[n(w_o,j+1)=\text{leftChild}(n(w_o,j))]]\cdot {\mathbf{u}}_{n(w_o,j)}^{\top }{\mathbf{v}}_c\right)$$
among ,$\text{leftChild}(n)$ Is the node $n$ The left child of ： If $x$ It's true ,$[[x]]=1$; otherwise $[[x]]=-1$.

To calculate the given word in the above figure $w_c$ Generative word $w_3$ Take the conditional probability of . This needs to be $w_c$ The word of the vector ${\mathbf{v}}_c$ And from root to $w_3$ The path of （ The bold path in the figure ） Dot product between non leaf node vectors on , The path turns left 、 Traverse right and left ：

$$P(w_3\mid w_c)=\sigma ({\mathbf{u}}_{n(w_3,1)}^{\top }{\mathbf{v}}_c)\cdot \sigma (-{\mathbf{u}}_{n(w_3,2)}^{\top }{\mathbf{v}}_c)\cdot \sigma ({\mathbf{u}}_{n(w_3,3)}^{\top }{\mathbf{v}}_c)$$
from $\sigma (x)+\sigma (-x)=1$, It believes that based on arbitrary words $w_c$ Generate a vocabulary $\mathcal{V}$ The sum of conditional probabilities of all words in is 1：${\sum }_{w\in \mathcal{V}}P(w\mid w_c)=1.$

In a binary tree structure ,$L(w_o)-1$ About and $\mathcal{O}({\text{log}}_2|\mathcal{V}|)$ It's an order of magnitude . When the vocabulary size $\mathcal{V}$ When a large , Compared with those without similar training , Use layering softmax The computational cost of each training step of is significantly reduced .

Summary

• Negative sampling constructs a loss function by considering independent events , These events involve both positive and negative cases . The calculation amount of training is linear with the number of noise words at each step .
• layered softmax Use the path from the root node to the leaf node in the binary tree to construct the loss function . The calculation cost of training depends on the logarithm of the size of the vocabulary .

3、 ... and 、 Data set for pre training word embedding

The dataset used here is Penn Tree Bank(PTB). The corpus is taken from “ Wall Street journal ” The article , Divided into training sets 、 Validation set and test set . In the original format , Each line of the text file represents a sentence separated by spaces . ad locum , We treat each word as a lexical element .

import math
import os
import random
import torch
from torch import nn
from d2l import torch as d2l
from torch.nn import functional as F

d2l.DATA_HUB['ptb'] = (d2l.DATA_URL + 'ptb.zip',
                       '319d85e578af0cdc590547f26231e4e31cdf1e42')


def read_ptb():
    """ take PTB The dataset is loaded into the list of text rows """
    data_dir = d2l.download_extract('ptb')
    # Read the training set.
    with open(os.path.join(data_dir, 'ptb.train.txt')) as f:
        raw_text = f.read()
    return [line.split() for line in raw_text.split('\n')]

• Building a vocabulary , Less than 10 The second word will be written by “<unk>” Lexical substitution .

sentences = read_ptb() # sentences Count : 42069
vocab = d2l.Vocab(sentences, min_freq=10) # vocab size: 6719

1. Down sampling

Text data usually has “the”、“a” and “in” And other high-frequency words , These words provide little useful information . Besides , A lot of （ high frequency ） Words will make the training speed very slow . therefore , When training words are embedded in the model , High frequency words can be down sampled . That is, every word in the dataset $w_i$ Will be discarded with probability

$$P(w_i)=\max \left(1-\sqrt{\frac{t}{f(w_i)}},0\right)$$
among ,$P(w_i)$ Refers to the probability of being discarded ,$f(w_i)$ Refer to words $w_i$ Frequency of occurrence in the dataset , Constant $t$ It's a super parameter. （ The following code is set to $10^{-4}$）. Only when $f(w_i)>t$ when ,（ high frequency ） word $w_i$ Can be discarded ,$f(w_i)$ The higher the , The higher the probability of being discarded .

• Down sampling high-frequency words

def subsample(sentences, vocab):
    """ Down sampling high-frequency words """
    #  Exclude unknown lexical elements '<unk>'
    sentences = [[token for token in line if vocab[token] != vocab.unk]
                 for line in sentences]
    counter = d2l.count_corpus(sentences)
    num_tokens = sum(counter.values())

    #  If word elements are preserved during downsampling , Then return to True
    # counter[token]:token Frequency of ;num_tokens： The total token Number ( It doesn't contain <unk>)
    def keep(token):
        return(random.uniform(0, 1) <
               math.sqrt(1e-4 / counter[token] * num_tokens))
    
    return ([[token for token in line if keep(token)] for line in sentences],
            counter)

subsampled, counter = subsample(sentences, vocab)

• After down sampling , The number of samples of high-frequency words will be significantly reduced , The sampling number of low-frequency words will not change , Keep it all

def compare_counts(token):
    return (f'"{
      token}" The number of ：'
            f' Before ={
      sum([l.count(token) for l in sentences])}, '
            f' after ={
      sum([l.count(token) for l in subsampled])}')
''' def compare_counts(token): return (f'"{token}" The number of ：' f' Before ={counter[token]},' f' after ={d2l.count_corpus(subsampled)[token]}') '''
print(compare_counts('in'))
print(compare_counts('join'))
# "in" The number of ： Before =18000,  after =1191
# "join" The number of ： Before =45,  after =45

2. Extraction of head words and context words

The size of the context window is 1 To max_window_size The random value

def get_centers_and_contexts(corpus, max_window_size):
    """ return Skip-Gram The head word and context word of """
    centers, contexts = [], []
    for line in corpus:
        #  To form “ Central word - Context words ” Yes , Each sentence should have at least 2 Word 
        if len(line) < 2:
            continue
        centers += line
        for i in range(len(line)):  #  In the middle of the context window i
            window_size = random.randint(1, max_window_size)
            indices = list(range(max(0, i - window_size),
                                 min(len(line), i + 1 + window_size)))
            #  Exclude the head word from the context word 
            indices.remove(i)
            contexts.append([line[idx] for idx in indices])
    # centers： contain corpus All the words ,contexts： Context of all headwords 
    return centers, contexts

3. Negative sampling

The noise words are sampled according to the predefined distribution , Sampling distribution through variables sampling_weights Pass on

class RandomGenerator:
    """ according to n Sample weights in {1,...,n} Randomly selected from """
    def __init__(self, sampling_weights):
        # Exclude
        self.population = list(range(1, len(sampling_weights) + 1))
        self.sampling_weights = sampling_weights
        self.candidates = []
        self.i = 0

    def draw(self):
        if self.i == len(self.candidates):
            #  cache k Random sampling results 
            self.candidates = random.choices(
                self.population, self.sampling_weights, k=10000)
            self.i = 0
        self.i += 1
        return self.candidates[self.i - 1]

For a pair of head words and context words , Random sampling $K$ individual （ In the experiment, there was no significant difference 5 individual ） Noise words . according to word2vec Suggestions in the paper , Put noise words $w$ The sampling probability of $P(w)$ Set to its relative frequency in the dictionary , Its power is 0.75.

def get_negatives(all_contexts, vocab, counter, K):
    """ Return the noise words in negative sampling """
    #  The index for 1、2、...（ Indexes 0 Is an unknown tag excluded from the vocabulary ）
    sampling_weights = [counter[vocab.to_tokens(i)]**0.75
                        for i in range(1, len(vocab))]
    all_negatives, generator = [], RandomGenerator(sampling_weights)
    for contexts in all_contexts:
        negatives = []
        while len(negatives) < len(contexts) * K:
            neg = generator.draw()
            #  Noise words cannot be context words 
            if neg not in contexts:
                negatives.append(neg)
        all_negatives.append(negatives)
    return all_negatives

sentences = read_ptb()
vocab = d2l.Vocab(sentences, min_freq=10)
subsampled, counter = subsample(sentences, vocab)
#  After down sampling , Map lexical elements to their indexes in the corpus 
corpus = [vocab[line] for line in subsampled]
all_centers, all_contexts = get_centers_and_contexts(corpus, 5)
all_negatives = get_negatives(all_contexts, vocab, counter, 5)

4. Load training instances in small batches

In small batches ,$i^{\mathrm{t}\mathrm{h}}$ Samples include headwords and their $n_i$ Context words and $m_i$ A noise word . Because the size of the context window is different ,$n_i+m_i$ For different $i$ Is different . therefore , For each sample , We are contexts_negatives Variables link their context words with noise words , And fill in zero , Until the connection length reaches max_len.

Mask variables masks In order to exclude filling in the calculation of loss . In order to distinguish positive and negative examples , Definition labels Variables separate context words from noise words . among labels Medium 1 Corresponding to contexts_negatives Positive examples of context words in ,0 Corresponding to negative example .

Input data Is a list with length equal to batch size , Each of these elements is composed of a central word center、 Its contextual words context And its noise words negative Sample of composition .

def batchify(data):
    """ Returns... With negative sampling Skip-Gram Small batch samples """
    max_len = max(len(c) + len(n) for _, c, n in data)
    centers, contexts_negatives, masks, labels = [], [], [], []
    for center, context, negative in data:
        cur_len = len(context) + len(negative)
        centers += [center]
        contexts_negatives += \
            [context + negative + [0] * (max_len - cur_len)]
        masks += [[1] * cur_len + [0] * (max_len - cur_len)]
        labels += [[1] * len(context) + [0] * (max_len - len(context))]
    return (torch.tensor(centers).reshape((-1, 1)), torch.tensor(
        contexts_negatives), torch.tensor(masks), torch.tensor(labels))

• Define function read PTB Data sets and returns data iterators and vocabularies

def load_data_ptb(batch_size, max_window_size, num_noise_words):
    """ download PTB Data sets , Then load it into memory """
    sentences = read_ptb()
    vocab = d2l.Vocab(sentences, min_freq=10)
    subsampled, counter = subsample(sentences, vocab)
    corpus = [vocab[line] for line in subsampled]
    all_centers, all_contexts = get_centers_and_contexts(corpus, max_window_size)
    all_negatives = get_negatives(all_contexts, vocab, counter, num_noise_words)

    class PTBDataset(torch.utils.data.Dataset):
        def __init__(self, centers, contexts, negatives):
            assert len(centers) == len(contexts) == len(negatives)
            self.centers = centers
            self.contexts = contexts
            self.negatives = negatives

        def __getitem__(self, index):
            return (self.centers[index], self.contexts[index],
                    self.negatives[index])

        def __len__(self):
            return len(self.centers)

    dataset = PTBDataset(all_centers, all_contexts, all_negatives)
    data_iter = torch.utils.data.DataLoader(dataset, batch_size, 
                                    shuffle=True, collate_fn=batchify)
    return data_iter, vocab

• Print the first small batch of the data iterator

data_iter, vocab = load_data_ptb(512, 5, 5)
for batch in data_iter:
    for name, data in zip(names, batch):
        print(name, 'shape:', data.shape)
    break

centers shape: torch.Size([512, 1])
contexts_negatives shape: torch.Size([512, 60])
masks shape: torch.Size([512, 60])
labels shape: torch.Size([512, 60])

Four 、 Preliminary training word2vec

batch_size, max_window_size, num_noise_words = 512, 5, 5
data_iter, vocab = d2l.load_data_ptb(batch_size, max_window_size, num_noise_words)

1. Forward propagation

In forward propagation ,Skip-Gram The input of includes the headword index center( Batch size ,1） And context and noise word index contexts_and_negatives（ Batch size ,max_len）. These two variables are first converted from the lexical index into vectors through the embedding layer , Then multiply their batch matrix to return the shape （ Batch size ,1,max_len） Output . Each element in the output is the dot product of the central word vector and the context or noise word vector .

def skip_gram(center, contexts_and_negatives, embed_v, embed_u):
    v = embed_v(center)
    u = embed_u(contexts_and_negatives)
    pred = torch.bmm(v, u.permute(0, 2, 1))
    return pred

2. Loss function

class SigmoidBCELoss(nn.Module):
    """ Binary cross entropy loss with mask """
    def __init__(self):
        super().__init__()

    def forward(self, inputs, target, mask=None):
        out = F.binary_cross_entropy_with_logits(
            inputs, target, weight=mask, reduction="none")
        return out.mean(dim=1)

loss = SigmoidBCELoss()

• Initialize model parameters

embed_size = 100
net = nn.Sequential(nn.Embedding(num_embeddings=len(vocab),
                                 embedding_dim=embed_size),
                    nn.Embedding(num_embeddings=len(vocab),
                                 embedding_dim=embed_size))

3. Training

def train(net, data_iter, lr, num_epochs, device=d2l.try_gpu()):
    def init_weights(m):
        if type(m) == nn.Embedding:
            nn.init.xavier_uniform_(m.weight)
    net.apply(init_weights)
    net = net.to(device)
    optimizer = torch.optim.Adam(net.parameters(), lr=lr)
    animator = d2l.Animator(xlabel='epoch', ylabel='loss', xlim=[1, num_epochs])
    #  Sum of normalized losses , Normalized loss number 
    metric = d2l.Accumulator(2)
    for epoch in range(num_epochs):
        timer, num_batches = d2l.Timer(), len(data_iter)
        for i, batch in enumerate(data_iter):
            optimizer.zero_grad()
            center, context_negative, mask, label = [data.to(device) for data in batch]

            pred = skip_gram(center, context_negative, net[0], net[1])
            l = (loss(pred.reshape(label.shape).float(), label.float(), mask)
                     / mask.sum(axis=1) * mask.shape[1])
            l.sum().backward()
            optimizer.step()
            metric.add(l.sum(), l.numel())
            if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:
                animator.add(epoch + (i + 1) / num_batches,
                             (metric[0] / metric[1],))
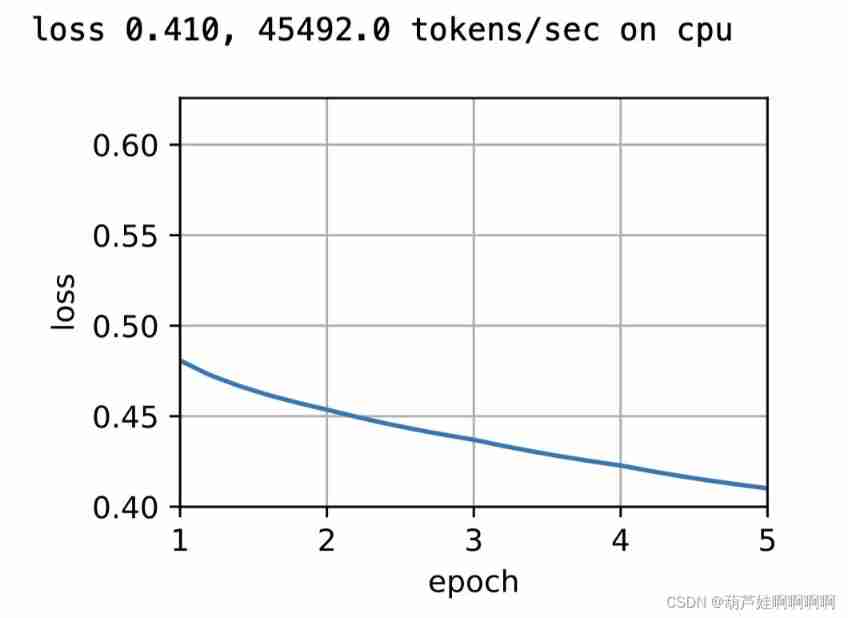
    print(f'loss {
      metric[0] / metric[1]:.3f}, '
          f'{
      metric[1] / timer.stop():.1f} tokens/sec on {
      str(device)}')
    
    
lr, num_epochs = 0.002, 5
train(net, data_iter, lr, num_epochs)

4. Word embedding

Training word2vec After the model , You can use the cosine similarity of the word vector in the trained model to find the word with the most similar semantics to the input word from the vocabulary .

def get_similar_tokens(query_token, k, embed):
    W = embed.weight.data
    x = W[vocab[query_token]]
    #  Calculate cosine similarity . increase 1e-9 To obtain numerical stability 
    cos = torch.mv(W, x) / torch.sqrt(torch.sum(W * W, dim=1) *
                                      torch.sum(x * x) + 1e-9)
    # torch.topk(cos, k=k+1)[1]  Return to the top of the similarity in descending order k+1 Corresponding indexes 
    topk = torch.topk(cos, k=k+1)[1].cpu().numpy().astype('int32')
    for i in topk[1:]:  #  Delete the input word 
        print(f'cosine sim={
      float(cos[i]):.3f}: {
      vocab.to_tokens(i)}')

get_similar_tokens('chip', 3, net[0])