当前位置:网站首页>Fibonacci sequence
Fibonacci sequence
2022-07-06 08:17:00 【m0_ fifty-two million three hundred and eighty-four thousand ni】
Fibonacci sequence is the most typical and relatively simple recursion , It is relatively simple to solve it with algorithmic thinking .
If you want to write an algorithm, you must first understand what Fibonacci sequence is , Fibonacci sequence (Fibonacci sequence), also called The golden section The sequence , Leonardo the mathematician · Fibonacci (Leonardo Fibonacci) Take rabbit breeding as an example , It is also called “ Rabbit Series ”, It refers to such a sequence :1、1、2、3、5、8、13、21、34、…… In Mathematics , The Fibonacci sequence is defined recursively as follows :F(0)=1,F(1)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N*) In Modern Physics 、 accurate Crystal structure 、 Chemistry and so on , Fibonacci sequence has direct application , So , American Mathematics will come from 1963 Published in 《 Fibonacci series Quarterly 》 A mathematical magazine in the name of , Used to publish research results in this field .( Source: Baidu Encyclopedia )
Recursion is a relatively difficult Algorithm , Now I only have some ideas of my own , Recursion is difficult because it has a complex process , Nest layer after layer , I often want to give up learning recursion because it is difficult to imagine the recursive process , But giving up is easy , But persistence must be cool , Learning Fibonacci made me have some ideas about recursion .
Recursion is a nested process layer after layer , My idea is to think only about the conditions for jumping out of the process , And loops that need recursion at first , The condition for Fibonacci sequence to jump out of the cycle is when n <= 2 when , return , If it is greater than 2 when , You need the sum of the first two numbers , Notice that here is the sum of the first two numbers , Instead of the sum of all the previous numbers , Because only the first two numbers need to be considered . These two numbers are not a specific number , All you need to know is how to calculate it , The previous number can be used feiBo(n-1) Instead of , The first two numbers can be used feiBo(n-2) Instead of , So calculate a greater than 2 The number of hours , As long as you need to return feiBo(n-1) + feiBo(n-2) that will do , There is no need to think about the complex recursive process . Of course, for the standardization of the code , It is necessary to judge whether the entered value is reasonable .
The end condition of recursion is :
if(n <= 2){
return 1;
}else{
return feiBo(n-1) + feiBo(n-2);
}Add constraints and complete the construction as ( The words are not too standard ):
class fei{
public int feiBo(int n){ // Back to a int type
if(n > 0){
if(n <= 2){
return 1;
}else{
return feiBo(n-1) + feiBo(n-2);
}
}else{
return 0;
}
}
}main The function and all the codes are ( In order to facilitate the constant test directly ):
public class demo17{
public static void main(String[] args) {
fei b = new fei();
int num = b.feiBo(8);
if(num != 0){
System.out.println(num);
}else{
System.out.println(" Incorrect input !");
}
}
}
class fei{
public int feiBo(int n){
if(n>=1){
if(n<=2){
return 1;
}else{
return feiBo(n-1)+feiBo(n-2);
}
}else{
return 0;
}
}
}
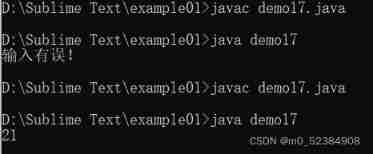
The test screenshot is :
边栏推荐
- The ECU of 21 Audi q5l 45tfsi brushes is upgraded to master special adjustment, and the horsepower is safely and stably increased to 305 horsepower
- Secure captcha (unsafe verification code) of DVWA range
- Pyqt5 development tips - obtain Manhattan distance between coordinates
- 24. Query table data (basic)
- Interview Reply of Zhuhai Jinshan
- The State Economic Information Center "APEC industry +" Western Silicon Valley will invest 2trillion yuan in Chengdu Chongqing economic circle, which will surpass the observation of Shanghai | stable
- 升级 TiDB Operator
- wincc7.5下载安装教程(Win10系统)
- Permutation and combination function
- "Designer universe" APEC design +: the list of winners of the Paris Design Award in France was recently announced. The winners of "Changsha world center Damei mansion" were awarded by the national eco
猜你喜欢
Online yaml to CSV tool
【云原生】手把手教你搭建ferry开源工单系统
A Closer Look at How Fine-tuning Changes BERT
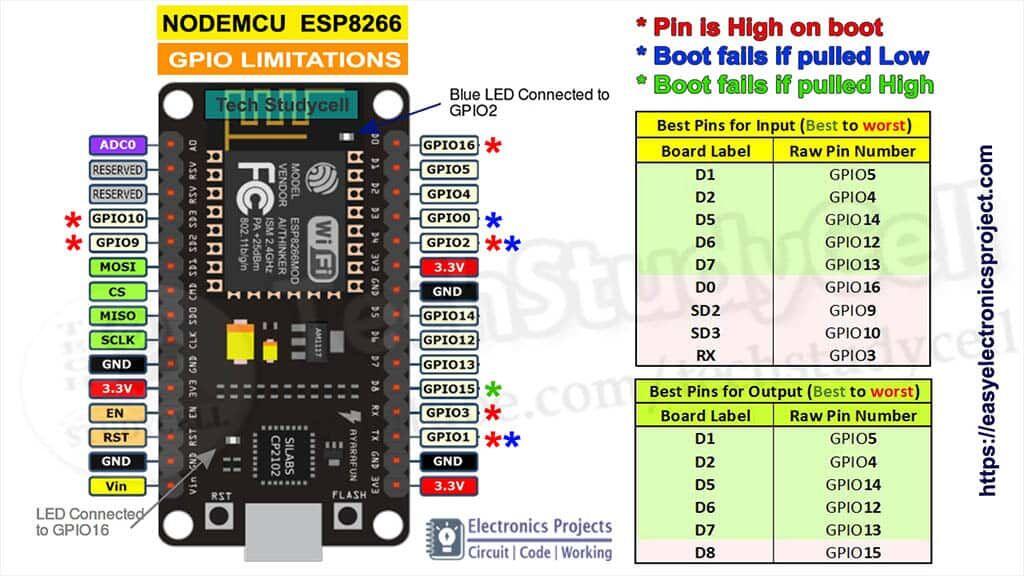
ESP系列引脚說明圖匯總

Circular reference of ES6 module
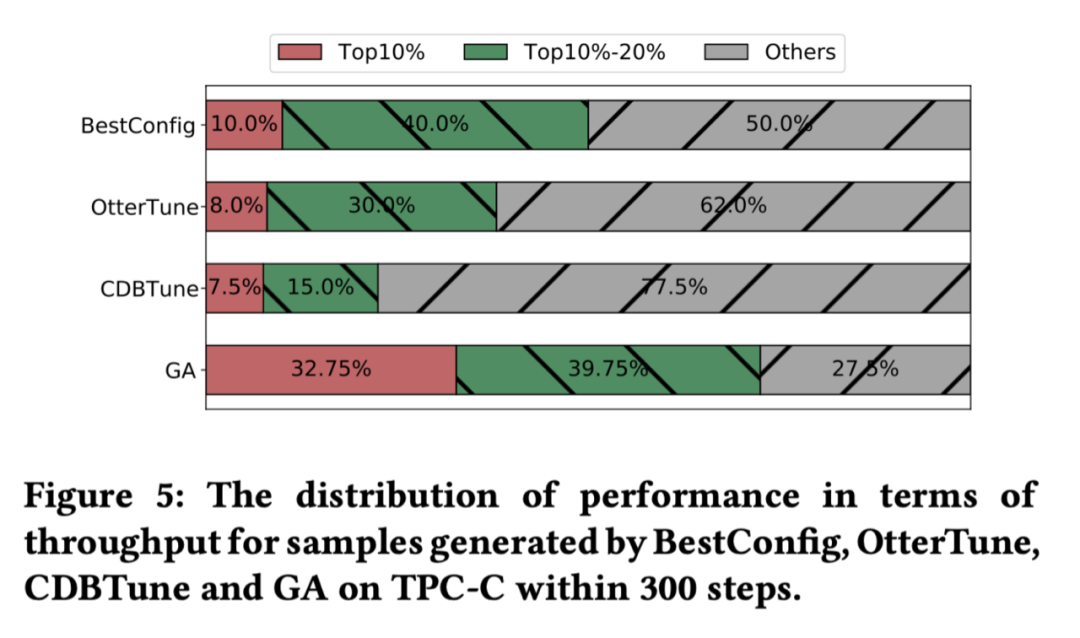
Personalized online cloud database hybrid optimization system | SIGMOD 2022 selected papers interpretation

Interview Reply of Zhuhai Jinshan

Learn Arduino with examples
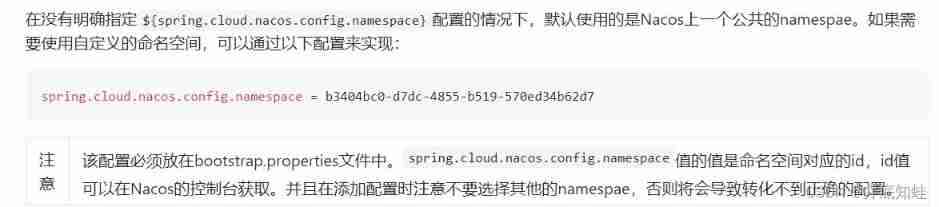
Nacos Development Manual
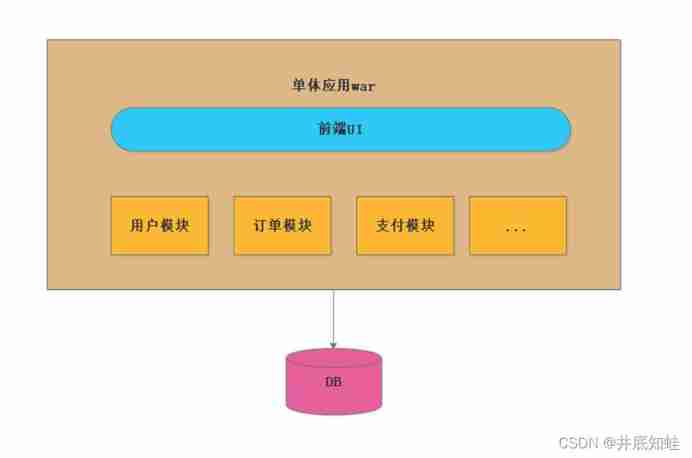
From monomer structure to microservice architecture, introduction to microservices
随机推荐
Hill sort c language
Notes on software development
Image fusion -- challenges, opportunities and Countermeasures
在 uniapp 中使用阿里图标
Introduction to backup and recovery Cr
【MySQL】数据库的存储过程与存储函数通关教程(完整版)
Epoll and IO multiplexing of redis
Artcube information of "designer universe": Guangzhou implements the community designer system to achieve "great improvement" of urban quality | national economic and Information Center
Configuring OSPF load sharing for Huawei devices
Machine learning - decision tree
On why we should program for all
Nft智能合约发行,盲盒,公开发售技术实战--拼图篇
matplotlib. Widgets are easy to use
MFC 给列表控件发送左键单击、双击、以及右键单击消息
Step by step guide to setting NFT as an ens profile Avatar
NFT smart contract release, blind box, public offering technology practice -- jigsaw puzzle
[redis] Introduction to NoSQL database and redis
All the ArrayList knowledge you want to know is here
C language custom type: struct
[cloud native] teach you how to build ferry open source work order system