[point cloud processing paper crazy reading classic version 11] - mining point cloud local structures by kernel correlation and graph pooling

Abstract

• problem ： The disorder of point clouds (unorder) It is still very challenging for semantic learning , In existing methods ,PointNet Good results are obtained by learning directly on the point set , however PointNet Local neighborhood information of the point cloud is not fully utilized , The local neighborhood information of point cloud contains fine-grained structural information , It can contribute to better semantic learning .
• Method ： Two new operations are proposed , In order to improve the PointNet Explore the efficiency of local structures .
• Technical details ：
  ① The first operation focuses on local 3D The geometric (geometric) structure , take point-set kernel Define as a group of learnable 3D points, these points Respond to a set of adjacent points , adopt kernel correlation Measure the geometric relationship between these adjacent points
  ② The second operation utilizes local high-dimensional features (feature) structure , Through point cloud 3D The position is calculated nearest-neighbor-graph, And then in nearest-neighbor-graph Feature aggregation recursively on (feature aggregation) Implement the operation .
• Code ：
  ① http://www.merl.com/research/license#KCNet
  ② https://github.com/ftdlyc/KCNet_Pytorch PyTorch edition It may not work , It's part of the code

introduction

• PointNet Directly aggregate the features of all points into global features , indicate PointNet Local structure mining that does not make full use of points fine-grained patterns： Every point of MLP Output only for 3D In a particular nonlinear partition of space 3D Rough coding of points .
• If MLP It's not just about “wether” Point of existence for coding , It can also be used for nonlinear 3D The points existing in the space partition are determined “what type of”（ for example , Corner and plane 、 Convex and concave points, etc ） Encoding , Is the more distinctive expression we expect .
• such “type” Information must come from 3D Learning in the local domain of the point on the surface of the target .
• Main contributions ：
  1. kernel correlation layer ——> Mining local geometry
  2. graph-based pooling layer ——> Mining local feature structure

Method

Learning on Local Geometric Structure

In this paper , With a point cloud local neighborhood As source, With learnable kernel( A set of points ) As reference, Thus, it represents the local structure / The shape of the type. In the point cloud registration task ,source and reference The points in the are fixed , But this article allows reference The point in changes , Through the study ( Back propagation ) The way to go more “ Fit ” shape . Unlike point cloud registration , We want to learn in a non transformational way reference, Not through optimal transformation . You can learn in this way kernel Point and convolution kernel It's the same , It responds to each point in the adjacent area , And capture local geometry in this perception domain , This perception domain is through kernel Functions and kernel wedth Decisive . With this configuration , The process of learning can be seen as finding a set of local geometric structures that can encode the most efficient and useful reference spot , And combine other parameters in the network to obtain the best learning performance .

To be specific , Definition with $M$ One can learn point-set kernel $\mathbf{\kappa }$ And with $N$ Current in point cloud of points anchor point ${\mathbf{x}}_i$ Between kernel correlation (KC) by ：
$$\mathrm{K}\mathrm{C}\left(\mathbf{\kappa },{\mathbf{x}}_i\right)=\frac{1}{|\mathcal{N}(i)|}\sum _{m=1}^M\sum _{n\in \mathcal{N}(i)}{\mathrm{K}}_{\sigma }\left({\mathbf{\kappa }}_m,{\mathbf{x}}_n-{\mathbf{x}}_i\right)$$
among ${\mathbf{\kappa }}_m$ yes kernel No $m$ Learning points ,$\mathcal{N}(i)$ yes anchor point ${\mathbf{x}}_i$ Neighborhood index of ,${\mathbf{x}}_n$ yes ${\mathbf{x}}_i$ One of the neighbor point.${\mathrm{K}}_{\sigma }(\cdot ,\cdot ):{\Re }^D\times {\Re }^D\to$$\Re$ Is arbitrary kernel function . In order to effectively store the local neighborhood of a point , We take each point as a vertex , Only adjacent vertices are connected by edges , So as to construct a KNNG.

Without losing generality , This article chooses Gaussian kernel：
$$K_{\sigma }(\mathbf{k},\mathbf{\delta })=\exp \left(-\frac{\Vert \mathbf{k}-\mathbf{\delta }{\Vert }^2}{2{\sigma }^2}\right)$$
among $\Vert \cdot \Vert$ Represents the Euclidean distance between two points ,$\sigma$ yes kernel Width , Control the influence of the distance between points .Gaussian kernel A good property of is that the distance between two points tends to be an exponential function , There is also one from each kernel Point to anchor point Of neighbor points Between soft-assignment( Derivable ).KC Yes kernel points and neighboring points Code the distance between , And increase the similarity of the two groups of point clouds in shape . It's worth noting that kernel width, Too big or too small will lead to unsatisfactory results , You can choose by experiment .

Given ：

1. Network loss function $\mathcal{L}$
2. The loss function is relative to each anchor point ${\mathbf{x}}_i$ Of $\mathrm{K}\mathrm{C}$ Derivative of back propagation from the top $d_i=\frac{\partial \mathcal{L}}{\partial \mathrm{K}\mathrm{C}\left(\mathbf{\kappa },{\mathbf{x}}_i\right)}$

This article provides each kernel point ${\kappa }_m$ Back propagation formula of ：
$$\frac{\partial \mathcal{L}}{\partial {\mathbf{\kappa }}_m}=\sum _{i=1}^N{\alpha }_i{d}_i\left[\sum _{n\in \mathcal{N}(i)}{\mathbf{v}}_{m,i,n}\exp \left(-\frac{{\Vert {\mathbf{v}}_{m,i,n}\Vert }^2}{2{\sigma }^2}\right)\right]$$
Middle point $x_i$ The normalization constant of is ${\alpha }_i=\frac{-1}{|\mathcal{N}(i)|{\sigma }^2}$, The local deviation vector is ${\mathbf{v}}_{m,i,n}={\mathbf{\kappa }}_m+{\mathbf{x}}_i-{\mathbf{x}}_n$.

Learning on Local Feature Structure

$\mathrm{K}\mathrm{C}$ It only acts on the front end of the network to extract local geometry . We also talked about before , By construction KNNG To get the information of adjacent points , This graph It can also be used to mine local feature structures in deeper layers . Affected convolution network can locally aggregate features , And through multiple pooling The layer gradually increases the inspiration of the receptive field , We walked along 3D neighborhood graph Edge recursively propagates and aggregates features , In order to extract local features in the upper layer .

One of our key ideas is neighbor points They tend to have similar geometric structures , So by neighborhood graph Propagation features can help learn more robust parts patterns. It is worth noting that , We specifically avoid changes in these layers above neighborhood graph Structure .

Make $\mathbf{X}\in {\Re }^{N\times K}$ Express graph pooling The input of , that KNNG Have adjacency matrix $\mathbf{W}\in$${\Re }^{N\times N}$, If the vertex $i$ And vertex $j$ There is an edge between , that $\mathbf{W}(i,j)=1$, otherwise $\mathbf{W}(i,j)=0$. Intuitively , Forming a local surface neighboring points Usually share similar features pattern. therefore , adopt graph pooling The operation aggregates features in the neighborhood of each point ：
$$\mathbf{Y}=\mathbf{P}\mathbf{X}$$
pooling The operation can be average pooling, It can also be max pooling.

Graph average pooling By using $\mathbf{P}\in {\Re }^{N\times N}$ As a normalized adjacency matrix, average all features in the neighborhood of a point ：
$$\mathbf{P}={\mathbf{D}}^{-1}\mathbf{W},$$
among $\mathbf{D}\in {\Re }^{N\times N}$ Is the degree matrix , The first $(i,j)$ individual entry $d_{i,j}$ Defined as ：

$$d_{i,j}=\{\begin{array}{ll}\mathrm{deg}(i),& \text{ if }i=j\\ 0,& \text{ otherwise }\end{array}$$
among $\mathrm{deg}(i)$ Is the vertex. $i$ Degree , Represents all connected to vertices $i$ The number of vertices of .

Graph max pooling(GM) Take the largest feature in the neighborhood of each vertex , stay $K$ Operate independently on three dimensions . So output $\mathbf{Y}$ Of the $(i,k)$ individual entry by ：
$$\mathbf{Y}(i,k)=\underset{n\in \mathcal{N}(i)}{\max }\mathbf{X}(n,k)$$
among $\mathcal{N}(i)$ Represent point set ${\mathbf{X}}_i$ Index of neighbors , from $\mathbf{W}$ It is calculated that .

experiment

Shape Classification

Network Configuration

As shown in the figure above ,KCNet share 9 layer . It is worth noting that ,KNN-Group Don't take part in training , It can even be calculated in advance , Its function is to construct adjacent points and feature aggregation , Play a structural role .

1. first floor ,kernel correlation, Take point coordinates as input , The output is local structural features , And then splice with the point coordinates .
2. Then the feature passes through the first two MLP Carry out feature learning point by point .
3. next graph pooling layer Aggregate the output point-by-point features into more robust local structural features , And the second two MLP The output is spliced .

The rest of the structure follows PointNet Very similar , except 1) Don't use Batchnorm,ReLU Used behind each full connection ;2)Dropout For the last full connection layer , Value is set to 0.5;

stay kernel computation and graph max pooling Use in 16-NN graph,kernel The number of $L$ by 32, Every kernel There are 16 A little bit , The initial value is set to $[-0.2,0.2]$,kernel width$\sigma =0.005$.

Results

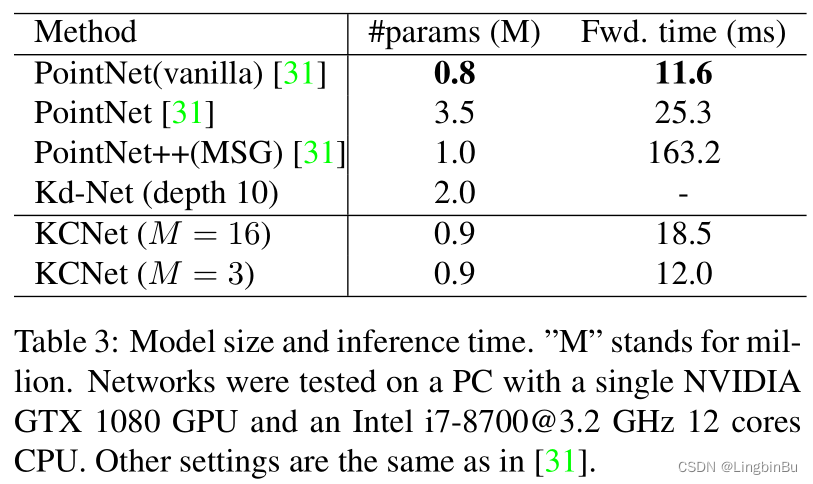
Part Segmentation

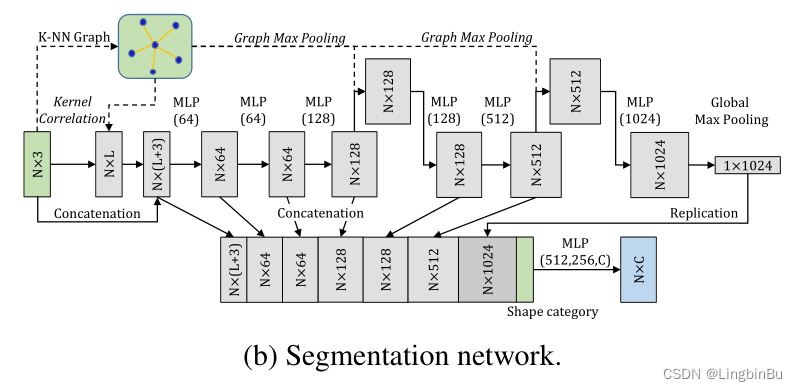
Network Configuration

Semantic Web has 10 layer , The local features captured by the features of different layers will be spliced with the global features and shape information . It doesn't use Batchnorm,Dropout Layer is used for full connection layer , The value is 0.3.18-NN graph be used for kernel computation and graph max pooling.kernel The quantity of is 16, Every kernel There is 18 A little bit , The initial value is $[-0.2,0.2]$ Between ,kernel width $\sigma =0.005$.

Results

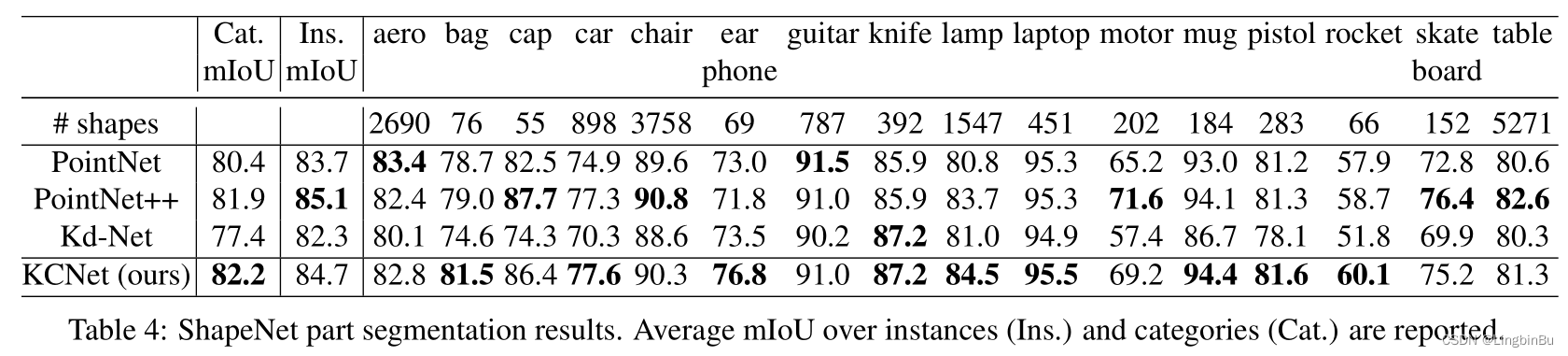
Ablation Study

Effectiveness of Kernel Correlation

Symmetric Functions

Effectiveness of Local Structures

Choosing Hyper-parameters

Robustness Test