当前位置:网站首页>第一讲:蛇形矩阵
第一讲:蛇形矩阵
2022-07-05 22:27:00 【奋斗吧!骚年!】
题目:AcWing 756. 蛇形矩阵
输入两个整数 n 和 m,输出一个 n 行 m 列的矩阵,将数字 1 到 n×m 按照回字蛇形填充至矩阵中。
具体矩阵形式可参考样例。
输入格式
输入共一行,包含两个整数 n 和 m。
输出格式
输出满足要求的矩阵。
矩阵占 n 行,每行包含 m 个空格隔开的整数。
数据范围
1≤n,m≤100
输入样例:
3 3
输出样例:
1 2 3
8 9 4
7 6 5
题目分析:
这道题主要使用x、y的偏移量
比如(x,y)如果想往下走那么就是(x+1,y+0),其它方向同理
如果换方向?
使用数组保存四个方向的偏移量,如果换方向数组下标+1模4即可。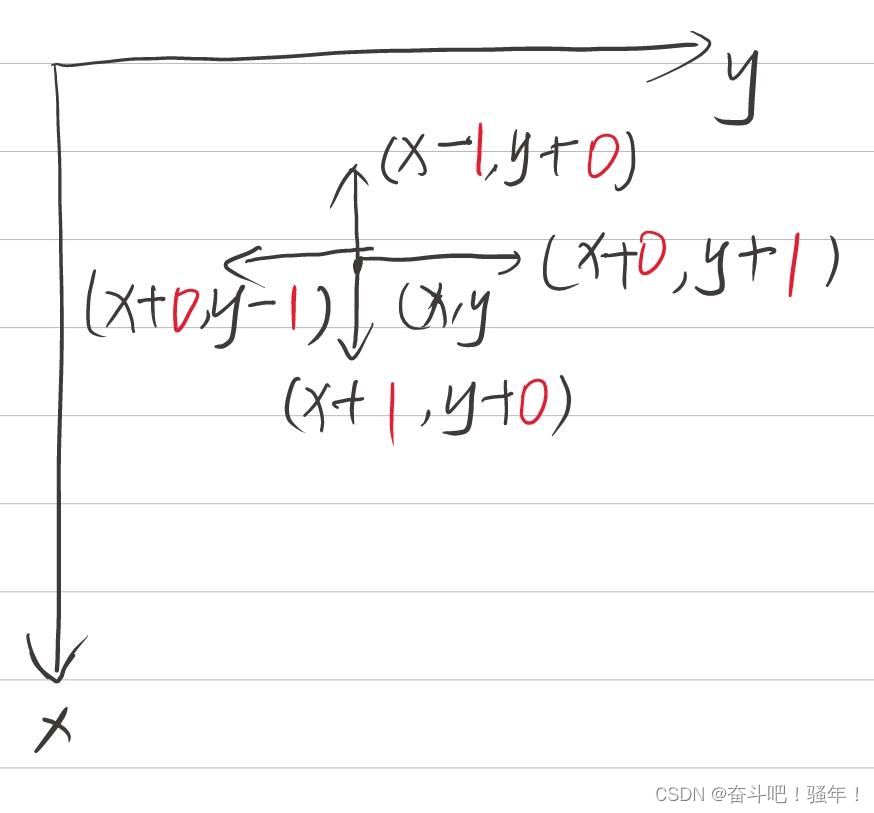
#include <iostream>
using namespace std;
const int N = 105;
int a[N][N];
int dx[]={
0,1,0,-1}; // 右下左上
int dy[]={
1,0,-1,0};
int main()
{
int n,m;
cin>>n>>m;
int x=0,y=0,d=0;
for(int i=1;i<=n*m;i++)
{
a[x][y]=i;
x+=dx[d],y+=dy[d]; // 进行移动
if(x<0||y<0||x>=n||y>=m||a[x][y])
{
x-=dx[d],y-=dy[d]; //如果移动失败需要恢复原状
d=(d+1)%4;
x+=dx[d],y+=dy[d]; // 再次移动
}
}
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)cout<<a[i][j]<<' ';
cout<<endl;
}
return 0;
}
边栏推荐
- C language - structural basis
- 2022 Software Test Engineer salary increase strategy, how to reach 30K in three years
- 记录几个常见问题(202207)
- Business learning of mall order module
- How to develop and introduce applet plug-ins
- The countdown to the launch of metaverse ape is hot
- Win11 runs CMD to prompt the solution of "the requested operation needs to be promoted"
- Overriding equals() & hashCode() in sub classes … considering super fields
- New 3D particle function in QT 6.3
- 509. Fibonacci Number. Sol
猜你喜欢

如何快速体验OneOS

A trip to Suzhou during the Dragon Boat Festival holiday

Navigation day answer applet: preliminary competition of navigation knowledge competition
What if the files on the USB flash disk cannot be deleted? Win11 unable to delete U disk file solution tutorial

The simple problem of leetcode is to split a string into several groups of length K

Database recovery strategy
Postman核心功能解析-参数化和测试报告
Damn, window in ie open()
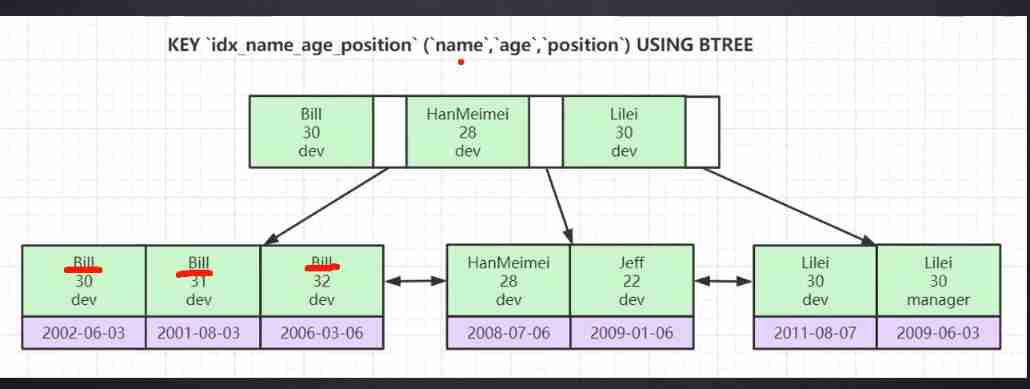
Talking about MySQL index
90后测试员:“入职阿里,这一次,我决定不在跳槽了”
随机推荐
The statistics of leetcode simple question is the public string that has appeared once
了解 Android Kotlin 中 DataStore 的基本概念以及为什么应该停止在 Android 中使用 SharedPreferences
90后测试员:“入职阿里,这一次,我决定不在跳槽了”
Wonderful review of the digital Expo | highlight scientific research strength, and Zhongchuang computing power won the digital influence enterprise award
Business learning of mall commodity module
Metaverse Ape获Negentropy Capital种子轮融资350万美元
Index optimization of performance tuning methodology
Cobaltstrike builds an intranet tunnel
Assign the output of a command to a variable [repeat] - assigning the output of a command to a variable [duplicate]
Go language learning tutorial (XV)
Win11缺少dll文件怎么办?Win11系统找不到dll文件修复方法
[groovy] mop meta object protocol and meta programming (Introduction to groovyobject interface | introduction to metaclass | implementation of class methods using groovyobject invokemethod)
Business learning of mall order module
Hcip day 16
Pl/sql basic syntax
ESP32 hosted
Granularity of blocking of concurrency control
Meituan dynamic thread pool practice ideas, open source
The code generator has deoptimised the styling of xx/typescript. js as it exceeds the max of 500kb
Promql demo service