当前位置:网站首页>1330: [example 8.3] minimum steps
1330: [example 8.3] minimum steps
2022-07-05 15:03:00 【A program ape who beats the keyboard violently】
1330:【 example 8.3】 Minimum steps
The time limit : 1000 ms Memory limit : 65536 KB
Submission number : 13863 Passing number : 7606
【 Title Description 】
In all kinds of chess , The way a piece moves is always certain , For example, in Chinese chess, the horse walks “ Japan ”. One primary school student thought that if a horse could walk in two ways, it would be more interesting , therefore , He stipulated that the horse can press “ Japan ” go , You can walk like an elephant “ field ” word . His deskmate usually likes to play go , It's interesting to know this later , Just want to try , In a (100×100) Choose any two points on your Go board A、B,A Point on the sunspot ,B Point on the white , For two horses . Chess pieces can be pressed “ Japan ” Word walk , You can also press “ field ” Word walk , Two people walk on a dark horse , A white horse . Who walks to the upper left corner with the least number of steps? The coordinate is (1,1) At the same time , Who wins . Now he asks you for help , Here you are. A、B The coordinates of two points , Want to know two positions to (1,1) Point to the minimum number of possible steps .
【 Input 】
A、B The coordinates of two points .
【 Output 】
Minimum steps .
【 sample input 】
12 16
18 10【 sample output 】
8
9【 Algorithm analysis 】
because A、B Two points are input randomly , Therefore, the mathematical law of calculating the minimum number of steps cannot be found , It can only be solved by breadth first search .
(1) Determine the starting point
from (n,m) Start with a breadth first search , Can be found from (n,m) The minimum number of steps to all reachable points on the chessboard . What is required in the question is the dark horse (x1,yy1) And white horse (x2,y2) arrive (1,1) The minimum number of steps of the target point . Although the starting points of the two paths are different , But their destination is the same . If we will end (1,1) As a starting point , In this way, you only need one breadth first search to get (x1,yy1) and (x2,y2) arrive (1,1) The minimum number of steps .
(2) data structure
set up queue—— queue , Storage slave (1,1) Reachable point (queue[k][1..2]) And the minimum number of steps required to reach this point (queue[k][3])(0
k
192+1). The first pointer of the queue is head, The tail pointer is tail. At the beginning ,queue Only one element in the is (1,1), The minimum number of steps is 0.
a—— Record (1,1) The minimum number of steps required to reach each point . obviously , The answer is a[x1][yy1] and a[x2][y2]. At the beginning ,a[1][1] by 0, All other element values are set to -1.
dx、dy—— Position increment array after moving . Ma you 12 Different expansion directions :
Horse walk “ Japan ”:
(n-2,m-1)(n-1,m-2)(n-2,m+1)(n-1,m+2)(n+2,m-1)(n+1,m-2)(n+2,m+1)(n+1,m+2)
Horse walk “ field ”:
(n-2,m-2)(n-2,m+2)(n+2,m-2)(n+2,m+2)
We will i The position increment in the direction is stored in the constant array dx[i]、dy[i] in (0
i
11):
int dx[12]={-1,-1,-1,1,2,2,2,2,1,-1,-2,-2},dy[12]={-1,-2,-2,-2,-2,-1,1,2,2,2,2,1};(3) constraint condition
(1) Don't go beyond the boundary . Because of all possible footholds of horses a Both in a Within the scope of , So once the horse goes out of bounds , Just put it a The value assigned to 0, Express “ Has been extended , And (1,1) It takes at least 0 Step ”. This seems absurd , But it can simply and effectively prevent the horse from falling into these boundary points again .
(2) This point has not been reached in previous extensions . If you have ever arrived , According to the principle of breadth first search , The number of steps required to reach this point previously must be less than the current number of steps , Therefore, there is absolutely no need to expand .
The resulting , The position of the horse after jumping (n,m) The constraint of whether you can join the team is a[n][m]
0.
(4) Algorithm flow
【AC Code 】
#include<algorithm>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iomanip>
#include<iostream>
#include<map>
#include<queue>
#include<string>
#include<vector>
using namespace std;
const int N=1e3+10;
inline int fread()
{
char ch=getchar();
int n=0,m=1;
while(ch<'0' or ch>'9')
{
if(ch=='-')m=-1;
ch=getchar();
}
while(ch>='0' and ch<='9')n=(n<<3)+(n<<1)+ch-48,ch=getchar();
return n*m;
}
int dx[12]={-1,-1,-1,1,2,2,2,2,1,-1,-2,-2},dy[12]={-1,-2,-2,-2,-2,-1,1,2,2,2,2,1},a[N][N],q[10000][4],x1,yy1,x2,y2,head=1,tail=1;// Initial position join the team
signed main()
{
memset(a,0xff,sizeof a),q[1][1]=q[1][2]=1,q[1][3]=0,x1=fread(),yy1=fread(),x2=fread(),y2=fread();//a Initialization of an array , Read the starting positions of black and white horses
while(head<=tail)
{
for(int i=0;i<12;i++)// enumeration 12 Expansion directions
{
int n=q[head][1]+dx[i],m=q[head][2]+dy[i];// Calculate Horse Press i Position after direction jump
if(n>0 and m>0)
if(a[n][m]==-1)// if (n,m) Meet the constraints
{
a[n][m]=q[head][3]+1,tail++,q[tail][1]=n,q[tail][2]=m,q[tail][3]=a[n][m];// Calculation (1,1) To (n,m) The minimum number of steps ,(1,1) to (n,m) Join the team with the minimum number of steps
if(a[x1][yy1]>0 and a[x2][y2]>0)// Output the solution of the problem
{
cout<<a[x1][yy1]<<"\n";
cout<<a[x2][y2]<<"\n";
return 0;
}
}
}
head++;
}
return 0;
}I like to use arrays to simulate queues
( It's not because I don't want to remember the queue's operation function ).

边栏推荐
- CPU design practice - Chapter 4 practice task 3 use pre delivery technology to solve conflicts caused by related issues
- Photoshop插件-动作相关概念-非加载执行动作文件中动作-PS插件开发
- Shanghai under layoffs
- Type declaration of all DOM elements in TS
- 【华为机试真题详解】欢乐的周末
- P1451 求细胞数量/1329:【例8.2】细胞
- Creation and use of thymeleaf template
- Magic methods and usage in PHP (PHP interview theory questions)
- easyOCR 字符识别
- 729. 我的日程安排表 I :「模拟」&「线段树(动态开点)」&「分块 + 位运算(分桶)」
猜你喜欢

30岁汇源,要换新主人了
Implement a blog system -- using template engine technology

超越PaLM!北大硕士提出DiVeRSe,全面刷新NLP推理排行榜
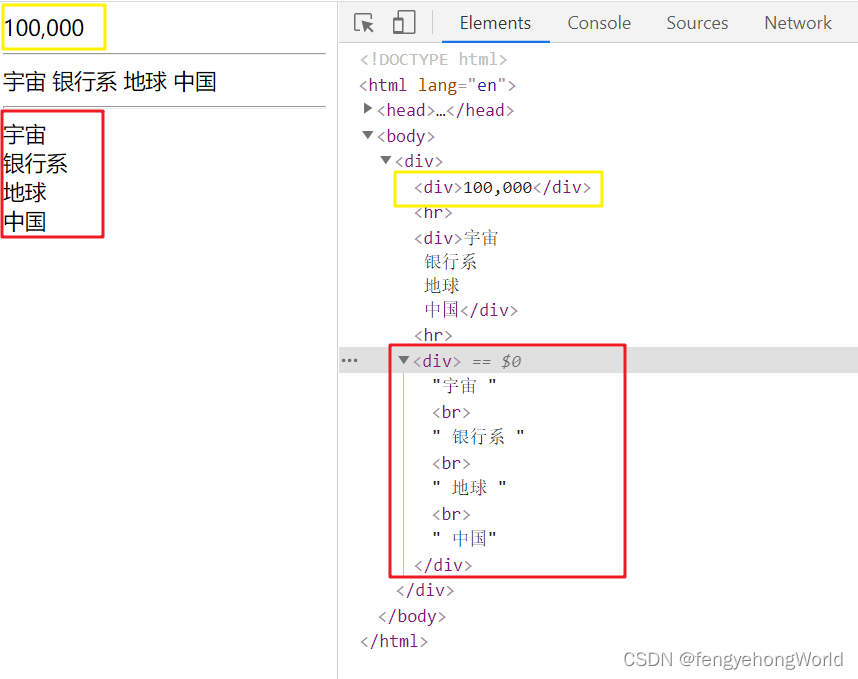
Thymeleaf uses background custom tool classes to process text
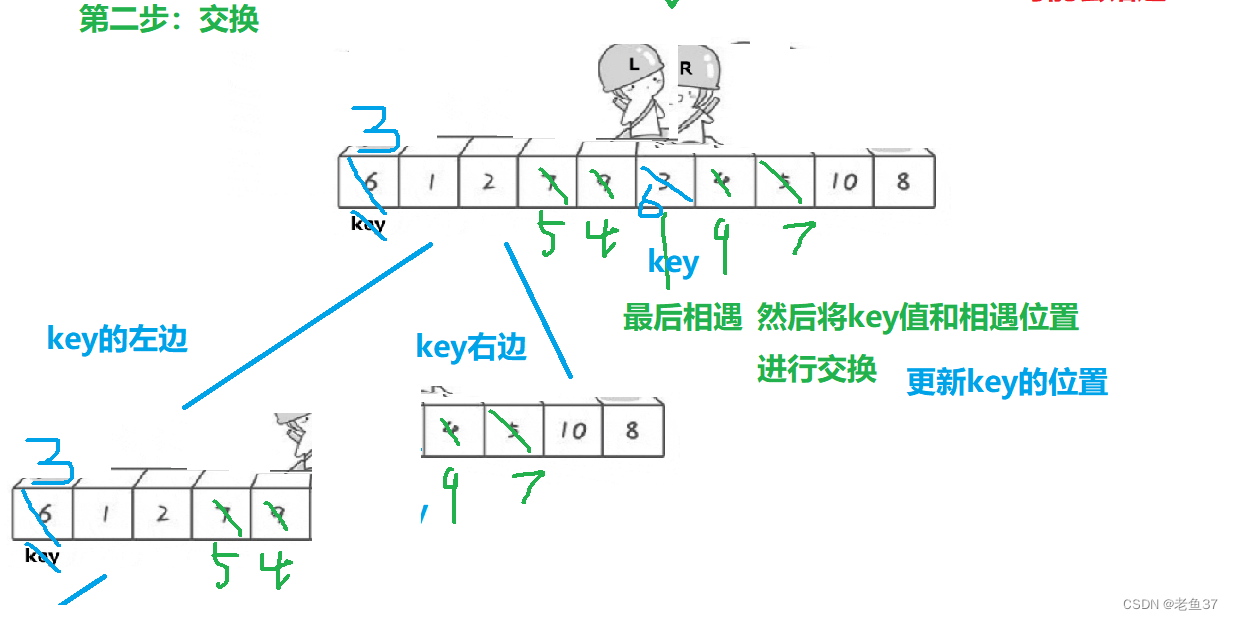
Super wow fast row, you are worth learning!
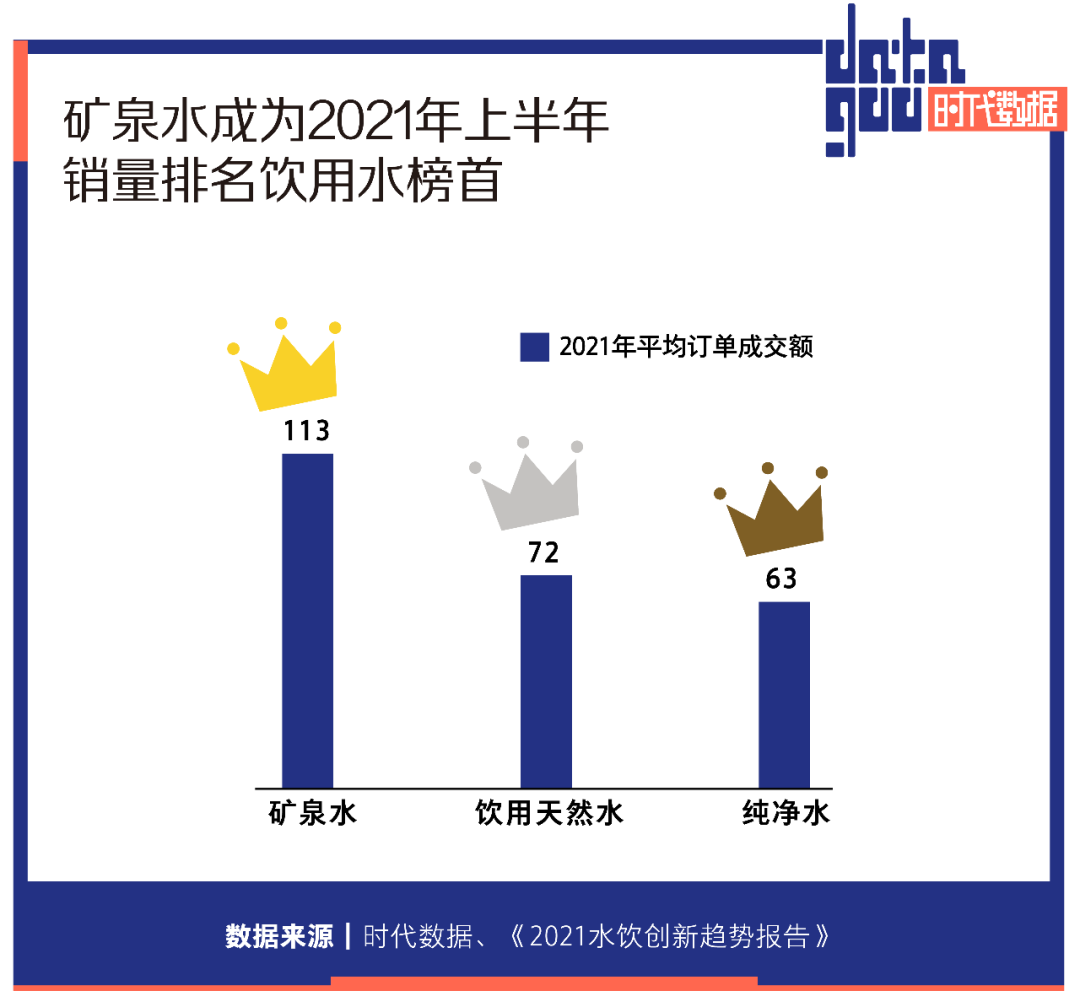
当代人的水焦虑:好水究竟在哪里?

Selection and use of bceloss, crossentropyloss, sigmoid, etc. in pytorch classification

数据库学习——数据库安全性

超级哇塞的快排,你值得学会!
How can I quickly check whether there is an error after FreeSurfer runs Recon all—— Core command tail redirection
随机推荐
Garbage collection mechanism of PHP (theoretical questions of PHP interview)
百亿按摩仪蓝海,难出巨头
外盘入金都不是对公转吗,那怎么保障安全?
Machine learning notes - gray wolf optimization
【华为机试真题详解】字符统计及重排
Photoshop plug-in action related concepts actionlist actiondescriptor actionlist action execution load call delete PS plug-in development
Leetcode: Shortest Word Distance II
Handwriting promise and async await
Ctfshow web entry explosion
Leetcode: Shortest Word Distance II
Photoshop插件-动作相关概念-ActionList-ActionDescriptor-ActionList-动作执行加载调用删除-PS插件开发
超越PaLM!北大碩士提出DiVeRSe,全面刷新NLP推理排行榜
漫画:优秀的程序员具备哪些属性?
Easyocr character recognition
Interview shock 62: what are the precautions for group by?
Two Bi development, more than 3000 reports? How to do it?
[recruitment position] infrastructure software developer
做研究无人咨询、与学生不交心,UNC助理教授两年教职挣扎史
Isn't it right to put money into the external market? How can we ensure safety?
数据库学习——数据库安全性
 k
k 0.
0.