Impulse response invariant method and bilinear transformation method for IIR filter design

前言

IIR（Infinite Impulse Response）Digital filter refers to an infinite impulse response digital filter,Because of its good amplitude-frequency response characteristics,are widely used in communication、控制、生物医学、振动分析、radar and sonar.

IIRThe filter can be designed by designing an analog filter,And then use the impulse response invariant method or the bilinear transformation method to design the digital filter.

注意：Some of the pictures in this blog post are from screenshots of the MOOC video,The course is Digital Signal Processing at Beihang University.

一、冲激响应不变法

h[n]与h(t)The relationship between can be derived from the sampling process,如图1所示：

图1 对h(t)The process of sampling

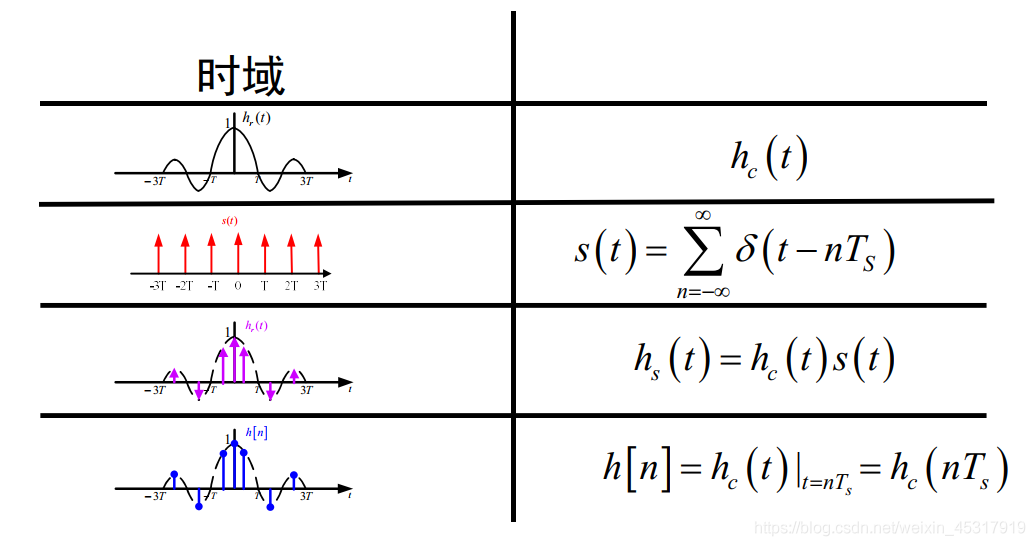
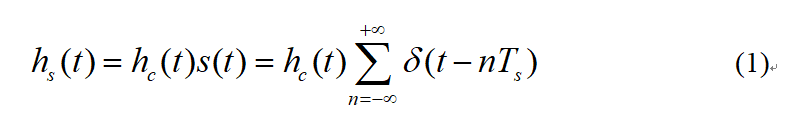
对式(1)Do the Laplace transform：

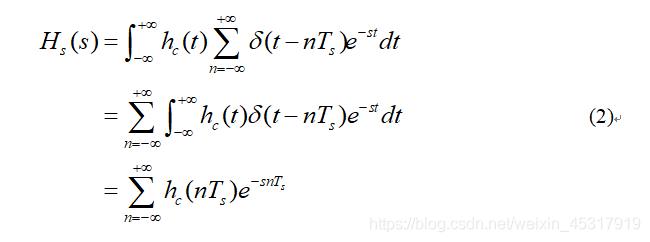
h[n]的Z变换为：

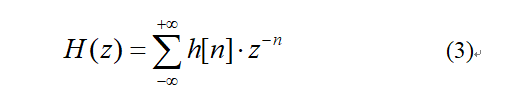
对比式(2)和式(3)可知,H(s)与H(z)的转换关系为：

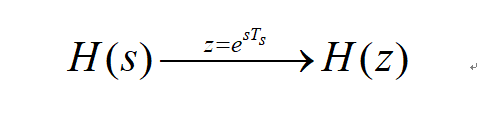
w与Ω的转换关系为：

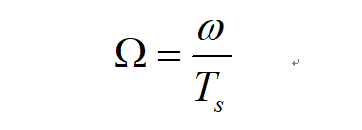
二、双线性变换法

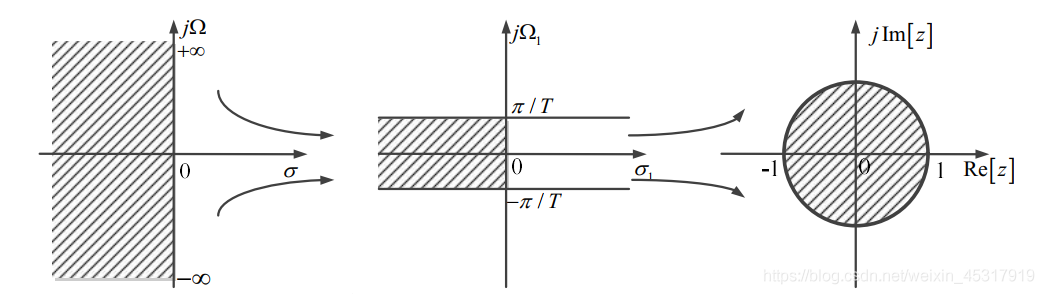
Bilinear transformation means that it has undergone two linear transformations,第一次是将ΩTransform from positive infinity to π/T,Negative infinity transforms to -π/T;第二次是将SThe left half-plane of the domain maps to Zwithin the unit circle of the domain. The bilinear transformation process is shown in Fig2所示.

图2 Bilinear transformation process

H(s)与H(z)的转换关系为：

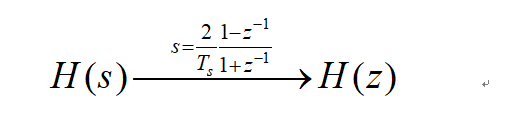
w与Ω的转换关系为：

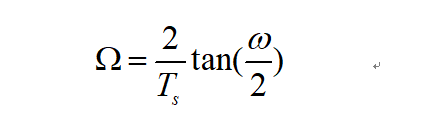
三、MATLAB代码

%% Impulse response invariant method to design Butterworth digital low-pass filter
T = 2;              % 设置采样周期
fs = 1/T;           % 采样频率
Wp = 0.30 * pi/T;   % 设置归一化通带和阻带截止频率
Ws = 0.35 * pi/T;
Ap = 20 * log10(1/0.8);   % Sets the passband maximum attenuation and stopband minimum attenuation
As = 20 * log10(1/0.18);

% 调用buttord函数确定巴特沃斯滤波器阶数
[N ,Wc] = buttord(Wp,Ws,Ap,As,'s');

% 调用butter函数设计巴特沃斯滤波器
[B ,A] = butter(N,Wc,'s');
W = linspace(0,pi,400*pi);  % 指定一段频率值
% Calculate the magnitude-frequency response of the analog filter
Hs = freqs(B,A,W);
% Invoke the shock response invariant method
[Bz,Az] = impinvar(B,A,fs);
% Return frequency response
Hz = freqz(Bz,Az,W);

%% 画图
figure;
subplot(1,2,1);
plot(W/pi,abs(Hs)/abs(Hs(1)));  % Plot the amplitude-frequency characteristic of the Butterworth analog filter
xlabel('频率/Hz');ylabel('幅值');title('巴特沃斯模拟滤波器');grid on;
subplot(1,2,2);
plot(W/pi,abs(Hz)/abs(Hz(1)));  % Plot the amplitude-frequency characteristic curve of the Butterworth digital low-pass filter
xlabel('频率/Hz');ylabel('幅值');title('巴特沃斯数字滤波器');grid on;

图3 巴特沃斯低通滤波器

%% Bilinear transformation method to design Butterworth digital band-stop filter
T = 2;          % 设置采样周期
fs = 1/T;       % 采样频率
wp = [0.30*pi,0.75*pi];
ws = [0.35*pi,0.65*pi];
Wp = (2/T)*tan(wp/2);   % 设置归一化通带和阻带截止频率
Ws = (2/T)*tan(ws/2);
Ap = 20 * log10(1/0.8);   % Sets the passband maximum attenuation and stopband minimum attenuation
As = 20 * log10(1/0.18);

% 调用buttord函数确定巴特沃斯滤波器阶数
[N ,Wc] = buttord(Wp,Ws,Ap,As,'s');

% 调用butter函数设计巴特沃斯滤波器
[B ,A] = butter(N,Wc,'stop','s');
W = linspace(0,pi,400*pi);  % 指定一段频率值
% Calculate the magnitude-frequency response of the analog filter
Hs = freqs(B,A,W);
% Invoke the bilinear transformation method
[Bz,Az] = bilinear(B,A,fs);
% Return frequency response
Hz = freqz(Bz,Az,W);

%% 画图
figure;
subplot(1,2,1);
plot(W/pi,abs(Hs));  % Plot the amplitude-frequency characteristic of the Butterworth analog filter
xlabel('频率/Hz');ylabel('幅值');title('巴特沃斯模拟滤波器');grid on;
subplot(1,2,2);
plot(W/pi,abs(Hz));  % Plot the amplitude-frequency characteristic curve of the Butterworth digital bandstop filter
xlabel('频率/Hz');ylabel('幅值');title('巴特沃斯数字滤波器');grid on;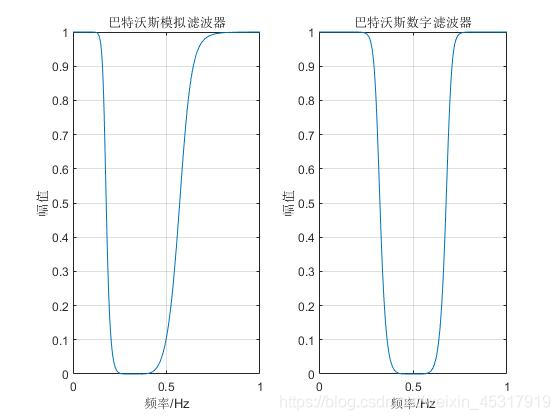

图4 巴特沃斯带阻滤波器

总结

冲激响应不变法的优缺点

优点：1）Fully mimics the unity impulse response of an analog filter,The instant domain approximation is good;2）The linear phase analog filter is still a linear phase digital filter obtained by the impulse response invariant method.

缺点：Aliasing effects of frequency response.

双线性变换法的优缺点

优点：Aliasing effects of the frequency response are avoided.

缺点：1）The original linear phase is no longer maintained,It is piecewise constant;2）Distortion occurs at the critical frequency points of each segment edge.

图 5 IIRDesign flow for digital filters

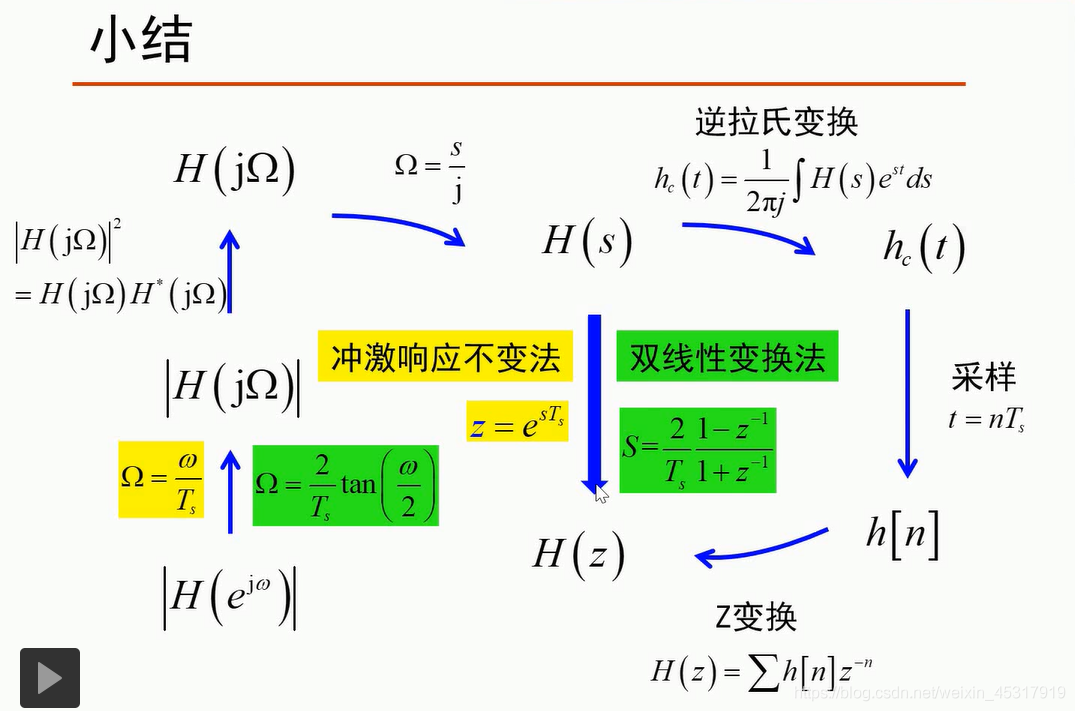
 首先,According to the amplitude-frequency response of the digital filter to be designed,Converted to the magnitude-frequency response of an analog filter,Then find the frequency response of a continuous system filterH(jΩ)Satisfy the amplitude-frequency response of the digital filter to be designed,Then find the system function of the continuous system that satisfies the amplitude-frequency responseH(s),obtained by derivationH(s)与H(z)conversion expression,得到H(z),That is, the system function of the discrete system.