当前位置:网站首页>深度学习(三)分类 理论部分
深度学习(三)分类 理论部分
2022-08-04 02:08:00 【Ali forever】
分类 理论部分
前言
本文将会围绕如何实现分类模型跟调节参数这个方面来进行阐述
一、反向传播
在深度学习神经网络中,最优化中一般会采用梯度下降法去调节我们的参数,但是由于神经网络的网络层过于复杂,求导十分困难,所以在计算机中就有一种十分方便的方法去降低计算的复杂度。
1.链式法则数学公式
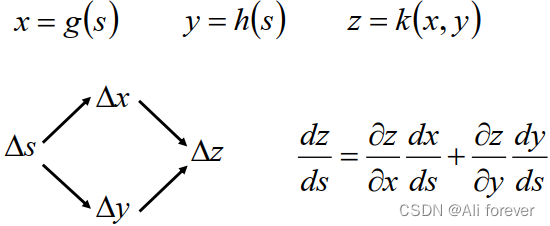
2.正向传播的过程
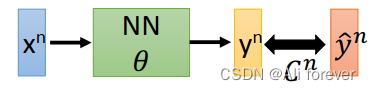
L ( θ ) = ∑ n = 1 N ( y n − y ^ n ) = ∑ n = 1 N C n ( θ ) L(\theta)=\sum_{n=1}^{N}(y^n-\hat{y}^n)=\sum_{n=1}^{N}C^n(\theta) L(θ)=n=1∑N(yn−y^n)=n=1∑NCn(θ)
∂ L ( θ ) ∂ w = ∑ n = 1 N ∂ C n ( θ ) ∂ w \frac{\partial L(\theta)}{\partial w}=\sum_{n=1}^{N}\frac{\partial C^n(\theta)}{\partial w} ∂w∂L(θ)=n=1∑N∂w∂Cn(θ)
这里我们挑出其中的一个C对权重w求偏导,根据链式法则我们可以把偏导拆分成:
∂ C ∂ w = ∂ z ∂ w ∗ ∂ C ∂ z \frac{\partial C}{\partial w}=\frac{\partial z}{\partial w}*\frac{\partial C}{\partial z} ∂w∂C=∂w∂z∗∂z∂C
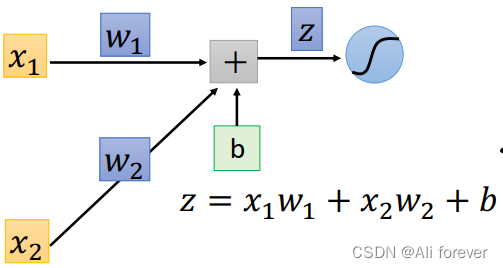
可以知道 ∂ z ∂ w 1 \frac{\partial z}{\partial w_1} ∂w1∂z= x 1 x_1 x1, ∂ z ∂ w 2 \frac{\partial z}{\partial w_2} ∂w2∂z= x 2 x_2 x2,这个过程我们叫做正向传播(Forward Pass),所以我们的问题集中在如何求解 ∂ C ∂ z \frac{\partial C}{\partial z} ∂z∂C中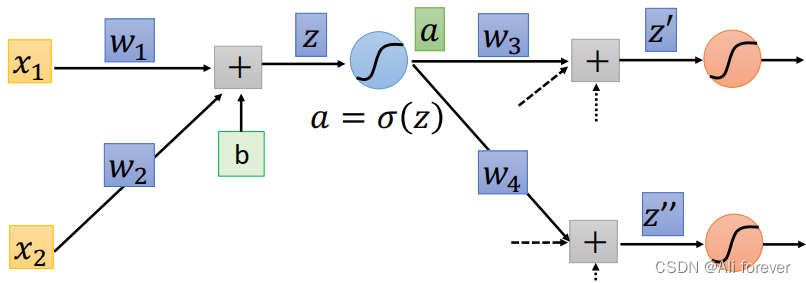
我们可以看到z通过一个激活函数可以得到一个新的结果叫做a,这是我们也可以通过链式法则去进行拆分:
∂ C ∂ z = ∂ a ∂ z ∗ ∂ C ∂ a \frac{\partial C}{\partial z}=\frac{\partial a}{\partial z}*\frac{\partial C}{\partial a} ∂z∂C=∂z∂a∗∂a∂C
可以知道 ∂ a ∂ z \frac{\partial a}{\partial z} ∂z∂a= σ ′ ( z ) \sigma'(z) σ′(z),那么如何求解 ∂ C ∂ a \frac{\partial C}{\partial a} ∂a∂C就变成一个非常困难的事情,因为根据链式法则
∂ C ∂ a = ∂ z ′ ∂ a ∗ ∂ C ∂ z ′ + ∂ z ′ ′ ∂ a ∗ ∂ C ∂ z ′ ′ \frac{\partial C}{\partial a}=\frac{\partial z'}{\partial a}*\frac{\partial C}{\partial z'}+\frac{\partial z''}{\partial a}*\frac{\partial C}{\partial z''} ∂a∂C=∂a∂z′∗∂z′∂C+∂a∂z′′∗∂z′′∂C
这时候如何我们继续推导下去公式就会变得异常复杂,并且如果后面成熟越来越多,将会成指数级别增长,所以我们不再进行正向传播了,接下来我们将进行反向传播(Backpropagation)
3.反向传播的过程
假设我们通过正向传播把所有的权重以及激活函数的导数都算出来了,那么结果将会是这样: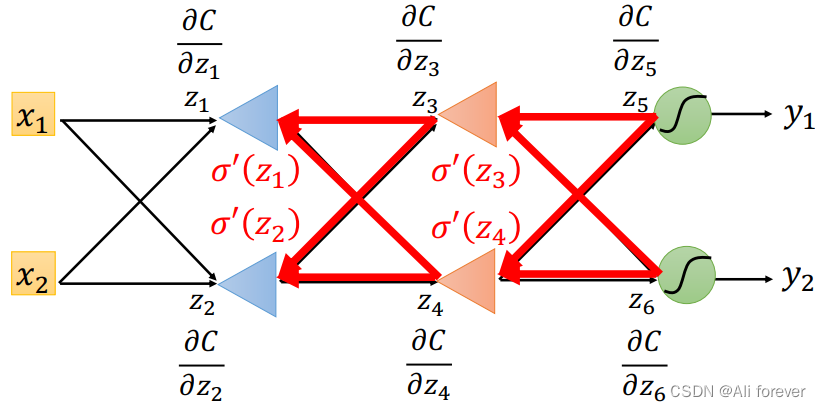
对于最后的输出层而言:
∂ C ∂ z 5 = ∂ y 1 ∂ z 5 ∗ ∂ C ∂ y 1 \frac{\partial C}{\partial z_5}=\frac{\partial y_1}{\partial z_5}*\frac{\partial C}{\partial y_1} ∂z5∂C=∂z5∂y1∗∂y1∂C ∂ C ∂ z 6 = ∂ y 2 ∂ z 6 ∗ ∂ C ∂ y 2 \frac{\partial C}{\partial z_6}=\frac{\partial y_2}{\partial z_6}*\frac{\partial C}{\partial y_2} ∂z6∂C=∂z6∂y2∗∂y2∂C这两项的结果都十分容易得出,得到这两项结果后,我们就可以继续从后往前计算我们之前正向传播所缺失的参数,在这里我们举个简单的例子:
∂ C ∂ a ( z 4 ) = ∂ z 5 ∂ a ( z 4 ) ∗ ∂ C ∂ z 5 + ∂ z 6 ∂ a ( z 4 ) ∗ ∂ C ∂ z 6 \frac{\partial C}{\partial a(z_4)}=\frac{\partial z_5}{\partial a(z_4)}*\frac{\partial C}{\partial z_5}+\frac{\partial z_6}{\partial a(z_4)}*\frac{\partial C}{\partial z_6} ∂a(z4)∂C=∂a(z4)∂z5∗∂z5∂C+∂a(z4)∂z6∗∂z6∂C
经过这样计算后,就可以把正向传播所缺失的项全部补齐了。
二、分类的预备知识(Classification)
在前面的内容里,我们介绍了如何进行回归的方法,但是不是所有问题都是回归问题,我们下面将会介绍另外一种问题,也就是分类问题
1.分类与回归的异同
分类与回归的相同点是:都是监督学习,都是对输入作出预测,然后得到预测值
分类与回归的不同点在以下几个方面:
输出不同
分类输出的是离散型变量,是一种定性输出,判断物体的类别,而回归输出的是连续型变量,是一种定量输出,得到输出值目的不同
分类的目的主要是去找到一个决策平面,对整个平面里面的数据进行分类,而回归的目的主要是去找到最优拟合,通过回归算法得到是一个最优拟合线,这个线条可以最好的接近数据集中的各个点。结果不同
分类的结果只有对错之分,而回归的结果则是以是否更接近真实值作为标准,而不是简单的判断对错。使用场景不同
分类可以用于手写签名的确认,人脸识别的确认,病症的确认等等。而回归则可以用于类似房价,天气的预测问题。
2.回归用作分类?
这种想法是源于通过回归得出一个预测值后,通过判断接近哪一个分类值,就判断是哪一个分类值,这种想法是错误的。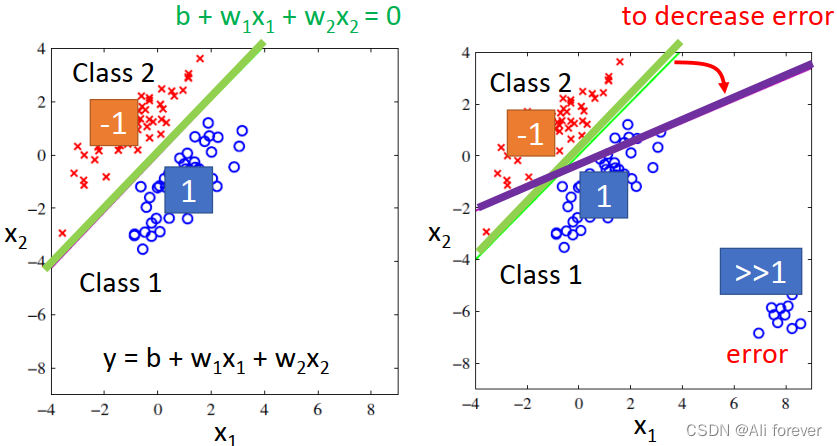
在这一幅图中,我们可以看到有远远大于1的值,根据我们上面的理论,这些远大于1的点会被判为1,但事实上他们是错误的点,这就导致了判断错误。
3.贝叶斯公式
我们以一个简单的抽球例子作为引入: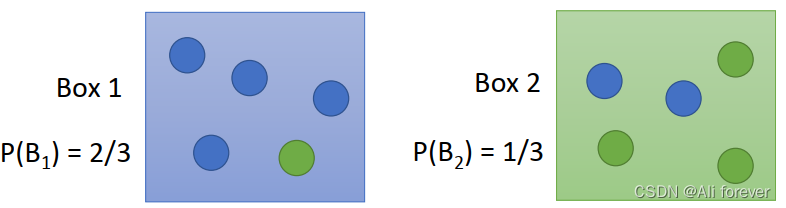
先验概率与后验概率:
先验概率:假设抽取Box1的概率是 2 3 \frac{2}{3} 32,抽取Box2的概率是 1 3 \frac{1}{3} 31,即P( B 1 B_1 B1)= 2 3 \frac{2}{3} 32,P( B 2 B_2 B2)= 1 3 \frac{1}{3} 31,这两个概率就是先验概率。
后验概率:当我们知道从 B 1 B_1 B1里面进行抽球,抽到蓝色的概率是P( B l u e ∣ B 1 Blue|B_1 Blue∣B1)= 4 5 \frac{4}{5} 54,抽到绿色的概率是P( G r e e n ∣ B 1 Green|B_1 Green∣B1)= 1 5 \frac{1}{5} 51
条件概率公式与全概率公式:
条件概率公式: P ( A B ) = P ( A ∣ B ) ∗ P ( B ) = P ( B ∣ A ) ∗ P ( A ) P(AB)=P(A|B)*P(B)=P(B|A)*P(A) P(AB)=P(A∣B)∗P(B)=P(B∣A)∗P(A)其中P(AB)是A与B的联合概率
全概率公式:如果事件 A 1 A_1 A1、 A 2 A_2 A2… … A i A_i Ai构成一个完备事件组,即它们两两互不相容,其和为全集,则有:
P ( B ) = ∑ n = 1 N P ( A i ) P ( B ∣ A i ) P(B)=\sum_{n=1}^{N}P(A_i)P(B|A_i) P(B)=n=1∑NP(Ai)P(B∣Ai)
贝叶斯公式
P ( B 1 ∣ B l u e ) = P ( B 1 , B l u e ) P ( B l u e ) = P ( B l u e ∣ B 1 ) ∗ P ( B 1 ) P ( B l u e ∣ B 1 ) ∗ P ( B 1 ) + P ( B l u e ∣ B 2 ) ∗ P ( B 2 ) P(B_1|Blue)=\frac{P(B_1,Blue)}{P(Blue)}=\frac{P(Blue|B_1)*P(B_1)}{P(Blue|B_1)*P(B_1)+P(Blue|B_2)*P(B_2)} P(B1∣Blue)=P(Blue)P(B1,Blue)=P(Blue∣B1)∗P(B1)+P(Blue∣B2)∗P(B2)P(Blue∣B1)∗P(B1)
三、生成模型与判别模型
监督学习中一般分成生成模型与判别模型,那么他们两种有什么异同呢?
1.生成模型(generative model)
源头导向型,关注数据时如何生成的,然后再对一个信号进行分类。(信号输入时,生成模型判断哪个类别最有可能产生这个信号,则这个信号就属于哪个类别。
我们利用一个简单的例子加以说明: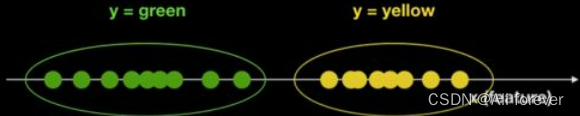
现在有一堆球,颜色信息已知为绿色和黄色两种,有且仅有这两种颜色,这里,球的颜色为y(目标变量),坐标轴上位置为特征X。我们想要知道,如果在坐标轴的某一位置x新放入一个球,这个球会是什么颜色的?
我们可以很轻松的计算出y的先验概率P(y),而后验概率P(x|y=green),
P(x|y=yellow)也能通过训练而进行估计,得到类似下面这样的结果: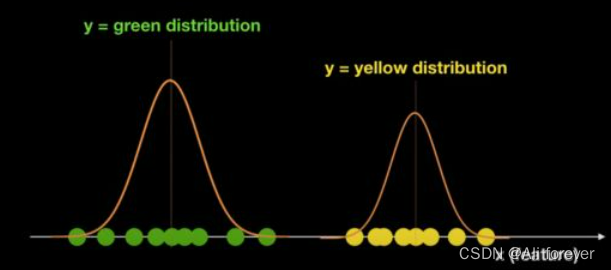
然后根据条件概率公式我们可以算出联合概率P(x,y=green),P(x,y=yellow)
如果是二分类问题就能通过判断哪个概率大得到最终的结果。
2.判别模型(Discriminative Model)
结果导向型,关注类别之间的差别,并不关心样本的数据时怎么生成的,根据样本之间的“分界线"来简单对给定的样本进行分类。
我们同样利用上面的例子进行说明: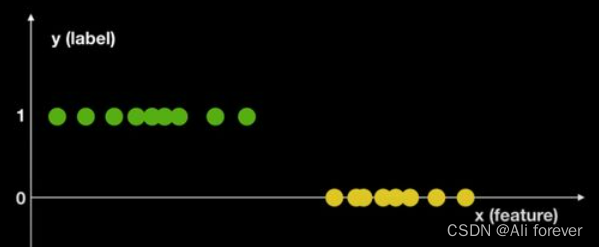
首先我们把这个图转换成这样,那么下一步我们就可以计算P(Y|X),通过计算我们可以通过一些算法得到一条分割线,来进行判别。
3.生成模型与判别模型之间的区别
- 特点
生成模型是以统计的角度去表示数据的分布情况,能反映同类数据的相似度。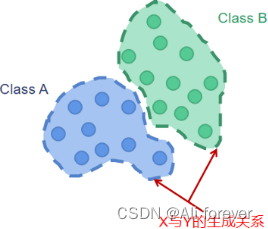
判别模型是寻找不同分类的最优分割面,反映数据的差异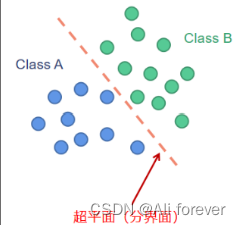
生成模型可以通过贝叶斯公式转化成判别模型,但是判别模型却无法转化为生成模型 - 优缺点
生成模型的优点:
- 能用于数据不完整的情况
- 收敛速度快,能更快地收敛到真实模型
- 存在隐变量时,仍然能使用,携带的信息比判别模型更多
- 过拟合的几率比较小,研究问题更加地灵活
判别模型的优点: - 结果很直观,能一眼看出某一类与其他类的区别
- 适用于更多的类别
- 判别模型更加简单,方便学习与训练
生成模型的缺点: - 需要大量的数据作为训练集,对数据很少的情况不友好
- 分布函数容易受到一些异常点的进入
- 对相似性很大的特征,容易产生假阳性
判别模型的缺点: - 黑盒操作,里面的变量关系不清晰,不可视
- 常见模型
生成模型:朴素贝叶斯分类器,马尔科夫模型,高斯混合模型,限制铂尔曼机
判别模型:逻辑回归,决策树,k近邻,线性回归,SVM,boosting - 常见用途
生成模型:NLP,医疗诊断
判别模型:图像文本分类,时间序列检测
四、高斯分布(Gaussian Distribution)与最大似然函数(Maximum Likelihood)
1.为什么使用高斯分布?
因为自然界中很多事件都是独立随机事件,这种随机变量接近于高斯分布,所以这已经假设了是独立随机事件,如果有严重的相关性我们一般不采用。
其次,在已知均值和方差的情况下高斯分布的熵是所有分布中最大的,数据分布未知时通常选择熵最大的模型
2.二维高斯分布公式
f μ , Σ ( x ) = 1 ( 2 π ) 2 D 1 ∣ Σ ∣ 1 2 e x p { − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) } f_{\mu,\Sigma}(x)=\frac{1}{(2\pi)^{2D}}\frac{1}{|\Sigma|^{\frac{1}{2}}}exp\{-\frac{1}{2}(x-\mu)^T{\Sigma}^{-1}(x-\mu)\} fμ,Σ(x)=(2π)2D1∣Σ∣211exp{ −21(x−μ)TΣ−1(x−μ)}
我们应当要知道高斯分布公式里面最重要的就是均值 μ \mu μ跟协方差矩阵 Σ \Sigma Σ,这两个参数决定了整个概率密度分布情况,我们会使用最大似然估计去计算得到他们
3.最大似然估计
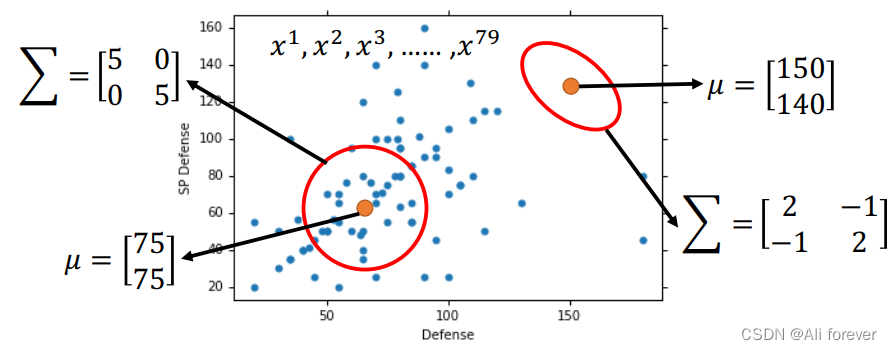
由于这里每选取一个点都会有不同的均值 μ \mu μ跟协方差矩阵 Σ \Sigma Σ,那我们可以将他们的概率密度函数全部相乘,得到:
L ( μ , Σ ) = f μ , Σ ( x 1 ) f μ , Σ ( x 2 ) . . . . . . f μ , Σ ( x n ) L(\mu,\Sigma)=f_{\mu,\Sigma}(x^1)f_{\mu,\Sigma}(x^2)......f_{\mu,\Sigma}(x^n) L(μ,Σ)=fμ,Σ(x1)fμ,Σ(x2)......fμ,Σ(xn)
然后我们的目标是得到
μ ∗ , Σ ∗ = arg max μ ∗ , Σ ∗ L ( μ , Σ ) \mu^*,\Sigma^*=\arg\max_{\mu^*,\Sigma^*} L(\mu,\Sigma) μ∗,Σ∗=argμ∗,Σ∗maxL(μ,Σ)
最后计算得到:
μ ∗ = 1 N ∑ n = 1 N x n , Σ ∗ = 1 N ∑ n = 1 N ( x n − μ ∗ ) ( x n − μ ∗ ) T \mu^*=\frac{1}{N}\sum_{n=1}^{N}x^n,\Sigma^*=\frac{1}{N}\sum_{n=1}^{N}(x^n-\mu^*)(x^n-\mu^*)^T μ∗=N1n=1∑Nxn,Σ∗=N1n=1∑N(xn−μ∗)(xn−μ∗)T
把最优解的参数全部算出来后,可以代入到原来的高斯分布中,由于后验概率服从高斯分布,我们可以代入数据,把结果计算出来。
4.高斯分布优化
由于协方差矩阵与输入的特征值数量有很大关系,如果特征值过多,较大的协方差矩阵会对结果有很大的影响,所以我们可以考虑共用一个协方差矩阵,从而降低误差。
下面进行加权平均,其中 α \alpha α为 μ 1 \mu_1 μ1的在所有 μ \mu μ中的占比。
Σ = α Σ 1 + ( 1 − α ) Σ 2 \Sigma = \alpha\Sigma_1+(1-\alpha)\Sigma_2 Σ=αΣ1+(1−α)Σ2
当取同一个 Σ \Sigma Σ的时候,我们会发现他的分解边界是一个线性模型。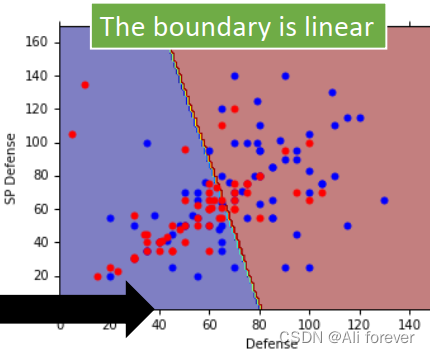
这是因为,我们的后验概率最后会转化成 P ( C 1 ∣ x ) = σ ( w x + b ) P(C_1|x)=\sigma(wx+b) P(C1∣x)=σ(wx+b),但是这样子本质上就是找出w跟b的值,如果用生成模型的话会浪费时间,接下来就会有另外一种方式去快速找到这个结果。
五、逻辑回归(Logistic Regression)
上面介绍判别模型的时候有介绍到,逻辑回归是一种判别模型,主要解决二分类的问题
1.函数集(Function Set)
z = ∑ i w i x i + b z=\sum_iw_ix_i+b z=i∑wixi+b
P w , b ( C 1 ∣ x ) = σ ( z ) = σ ( ∑ i w i x i + b ) P_{w,b}(C_1|x)=\sigma(z)=\sigma(\sum_iw_ix_i+b) Pw,b(C1∣x)=σ(z)=σ(i∑wixi+b)
2.评价函数的好坏(Goodness of a Function)

我们可以看到这么多个特征分别对应的类别,接下来我们要计算对于某个w跟b的一个概率密度函数
L ( w , b ) = f w , b ( x 1 ) f w , b ( x 2 ) ( 1 − f w , b ( x 3 ) ) . . . . . . f w , b ( x N ) L(w,b)=f_{w,b}(x^1)f_{w,b}(x^2)(1-f_{w,b}(x^3))......f_{w,b}(x^N) L(w,b)=fw,b(x1)fw,b(x2)(1−fw,b(x3))......fw,b(xN)
同样的道理我们调用最大似然估计求得最佳的w与b值,一般为了减低计算量,我们会采取取对数的方式,这样就把乘积转化为各项相加了
w ∗ , b ∗ = arg max w ∗ , b ∗ L ( w , b ) = arg min w ∗ , b ∗ − ln L ( w , b ) w^*,b^*=\arg\max_{w^*,b^*} L(w,b)=\arg\min_{w^*,b^*}-\ln L(w,b) w∗,b∗=argw∗,b∗maxL(w,b)=argw∗,b∗min−lnL(w,b)
接下来我们会构造交叉熵(cross entropy)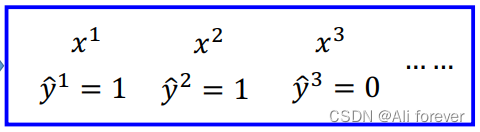
H ( p , q ) = − ∑ x p ( x ) ln ( q ( x ) ) H(p,q)=-\sum_xp(x)\ln(q(x)) H(p,q)=−x∑p(x)ln(q(x))
在这里p(x)代指的是实际分布,q(x)代指的是最大似然估计的分布,所以每一项可以变成这样:
− ln f w , b ( x 1 ) = − ( y ^ 1 ln f w , b ( x 1 ) + ( 1 − y ^ 1 ) ln ( 1 − f w , b ( x 1 ) ) ) -\ln f_{w,b}(x^1)=-(\hat{y}^1\ln f_{w,b}(x^1)+(1-\hat{y}^1)\ln (1-f_{w,b}(x^1))) −lnfw,b(x1)=−(y^1lnfw,b(x1)+(1−y^1)ln(1−fw,b(x1)))
总的交叉熵函数变成:
− ln L ( w , b ) = − ∑ n ( y ^ n ln f w , b ( x n ) + ( 1 − y ^ n ) ln ( 1 − f w , b ( x n ) ) ) -\ln L(w,b)=-\sum_n(\hat{y}^n\ln f_{w,b}(x^n)+(1-\hat{y}^n)\ln (1-f_{w,b}(x^n))) −lnL(w,b)=−n∑(y^nlnfw,b(xn)+(1−y^n)ln(1−fw,b(xn)))
交叉熵代表的是两个分布的接近程度,如果两个分布一模一样,则交叉熵为0,如果两个分布相差很大,则交叉熵很大。
3.找到最佳的函数(Find the best function)
− ln L ( w , b ) ∂ w i = − ∑ n ( y ^ n ln f w , b ( x n ) ∂ w i + ( 1 − y ^ n ) ln ( 1 − f w , b ( x n ) ) ∂ w i ) \frac{-\ln L(w,b)}{\partial w_i}=-\sum_n(\frac{\hat{y}^n\ln f_{w,b}(x^n)}{\partial w_i}+\frac{(1-\hat{y}^n)\ln (1-f_{w,b}(x^n))}{\partial w_i}) ∂wi−lnL(w,b)=−n∑(∂wiy^nlnfw,b(xn)+∂wi(1−y^n)ln(1−fw,b(xn)))
∂ ln f w , b ( x n ) ∂ w i = ∂ z ∂ w i ∂ ln f w , b ( x n ) ∂ z = x i ∗ 1 σ ( z ) ∗ σ ( z ) ∗ ( 1 − σ ( z ) ) \frac{\partial \ln f_{w,b}(x^n)}{\partial w_i}=\frac{\partial z}{\partial w_i}\frac{\partial\ln f_{w,b}(x^n)}{\partial z}=x_i*\frac{1}{\sigma(z)}*\sigma(z)*(1-\sigma(z)) ∂wi∂lnfw,b(xn)=∂wi∂z∂z∂lnfw,b(xn)=xi∗σ(z)1∗σ(z)∗(1−σ(z))
∂ ln ( 1 − f w , b ( x n ) ) ∂ w i = ∂ z ∂ w i ∂ ln ( 1 − f w , b ( x n ) ) ∂ z = x i ∗ 1 1 − σ ( z ) ∗ ( 1 − σ ( z ) ) ∗ ( σ ( z ) ) \frac{\partial \ln(1- f_{w,b}(x^n))}{\partial w_i}=\frac{\partial z}{\partial w_i}\frac{\partial\ln (1-f_{w,b}(x^n))}{\partial z}=x_i*\frac{1}{1-\sigma(z)}*(1-\sigma(z))*(\sigma(z)) ∂wi∂ln(1−fw,b(xn))=∂wi∂z∂z∂ln(1−fw,b(xn))=xi∗1−σ(z)1∗(1−σ(z))∗(σ(z))
∂ − ln L ( w , b ) ∂ w i = − ∑ n y ^ n ∗ x i n ∗ ( 1 − σ ( z ) ) − ( 1 − y ^ n ) ∗ x i n ∗ σ ( z ) = − ∑ n ( y ^ n − σ ( z ) ) ∗ x i n \begin{split} \frac{\partial -\ln L(w,b)}{\partial w_i}&=-\sum_n\hat{y}^n*x_i^n*(1-\sigma(z))-(1-\hat{y}^n)*x_i^n*\sigma(z)\\ &=-\sum_n(\hat{y}^n-\sigma(z))*x_i^n \end{split} ∂wi∂−lnL(w,b)=−n∑y^n∗xin∗(1−σ(z))−(1−y^n)∗xin∗σ(z)=−n∑(y^n−σ(z))∗xin
最后得出更新函数:
w i = w i − η ∑ n ( y ^ n − σ ( z ) ) ∗ x i n w_i=w_i-\eta\sum_n(\hat{y}^n-\sigma(z))*x_i^n wi=wi−ηn∑(y^n−σ(z))∗xin
对比线性回归与逻辑回归的更新函数,你会发现两者长得一模一样,只是逻辑回归的 y ^ n \hat{y}^n y^n只能取值0或者1,线性回归可以取很多不同的值。
4.逻辑回归的损失函数问题
在前面我们说到,逻辑回归选取的损失函数是交叉熵,而不是我们在线性回归中所提到均方差,这是为什么呢?
这是因为当 σ ( z ) \sigma(z) σ(z)=0或者1时,整个loss function的结果都为0,也就是说这两种情况下都会被判作收敛,出现假阳性问题,这是不可取的,所以我们不会采用均方差在逻辑回归中。
总结
本文介绍了分类的理论部分,希望大家能从中获取到想要的东西,下面附上一张思维导图帮助记忆。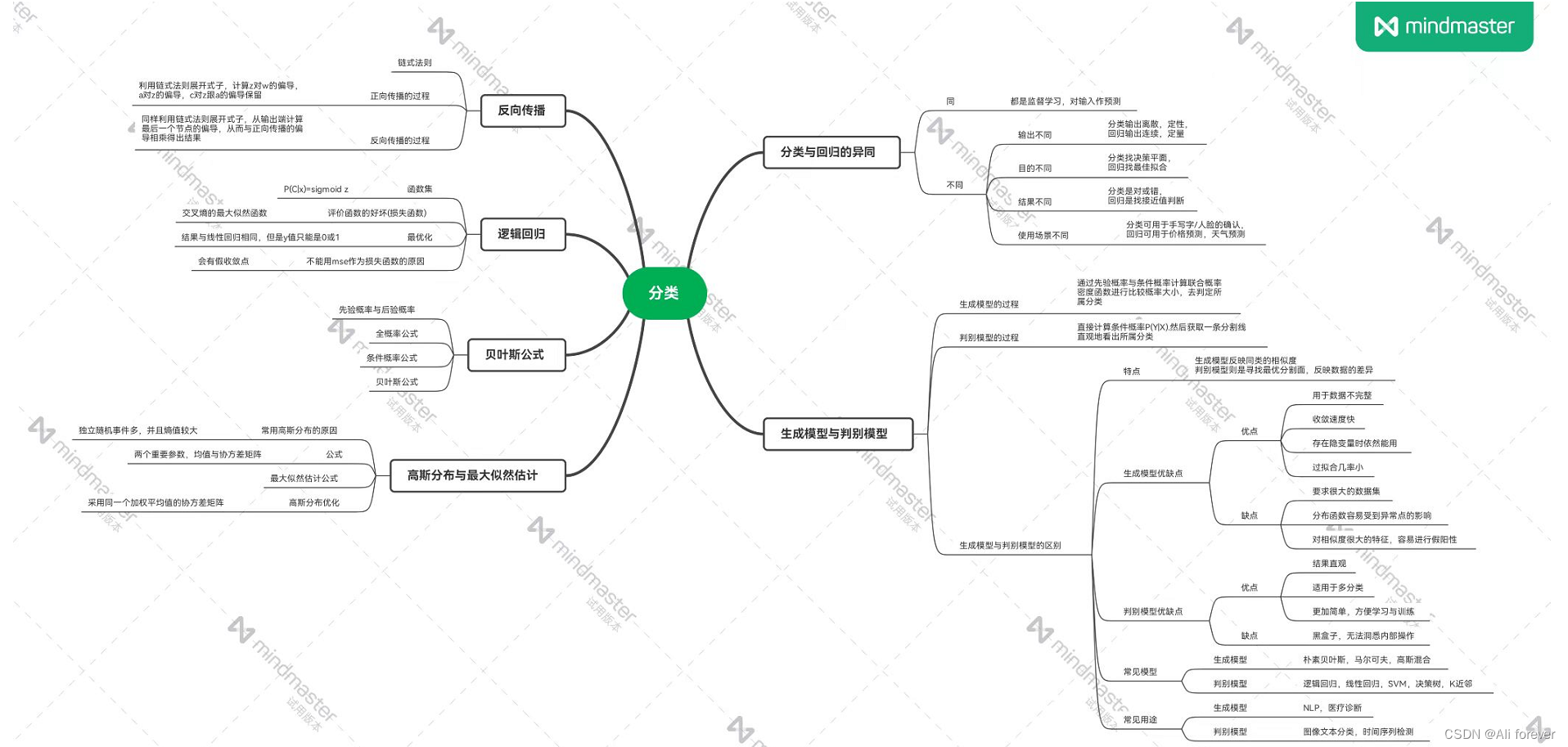
边栏推荐
- Example 035: Setting the output color
- Sticker Spelling - Memory Search / Shape Pressure DP
- Day13 Postman的使用
- Web APIs BOM- 操作浏览器:swiper 插件
- What is SVN (Subversion)?
- boot issue
- Priority_queue element as a pointer, the overloaded operators
- 各位大佬好,麻烦问一下flink cdc oracle写入doris的时候,发现cpu异常,一下下跑
- 大佬们,读取mysql300万单表要很长时间,有什么参数可以优惠,或者有什么办法可以快点
- Flask Framework Beginner-06-Add, Delete, Modify and Check the Database
猜你喜欢
工程制图复习题(带答案)
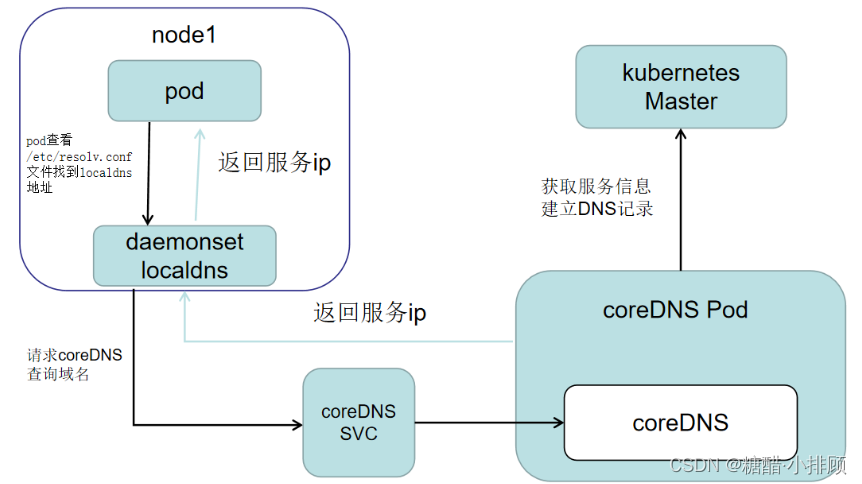
Kubernetes:(九)coredns(浪不动了)
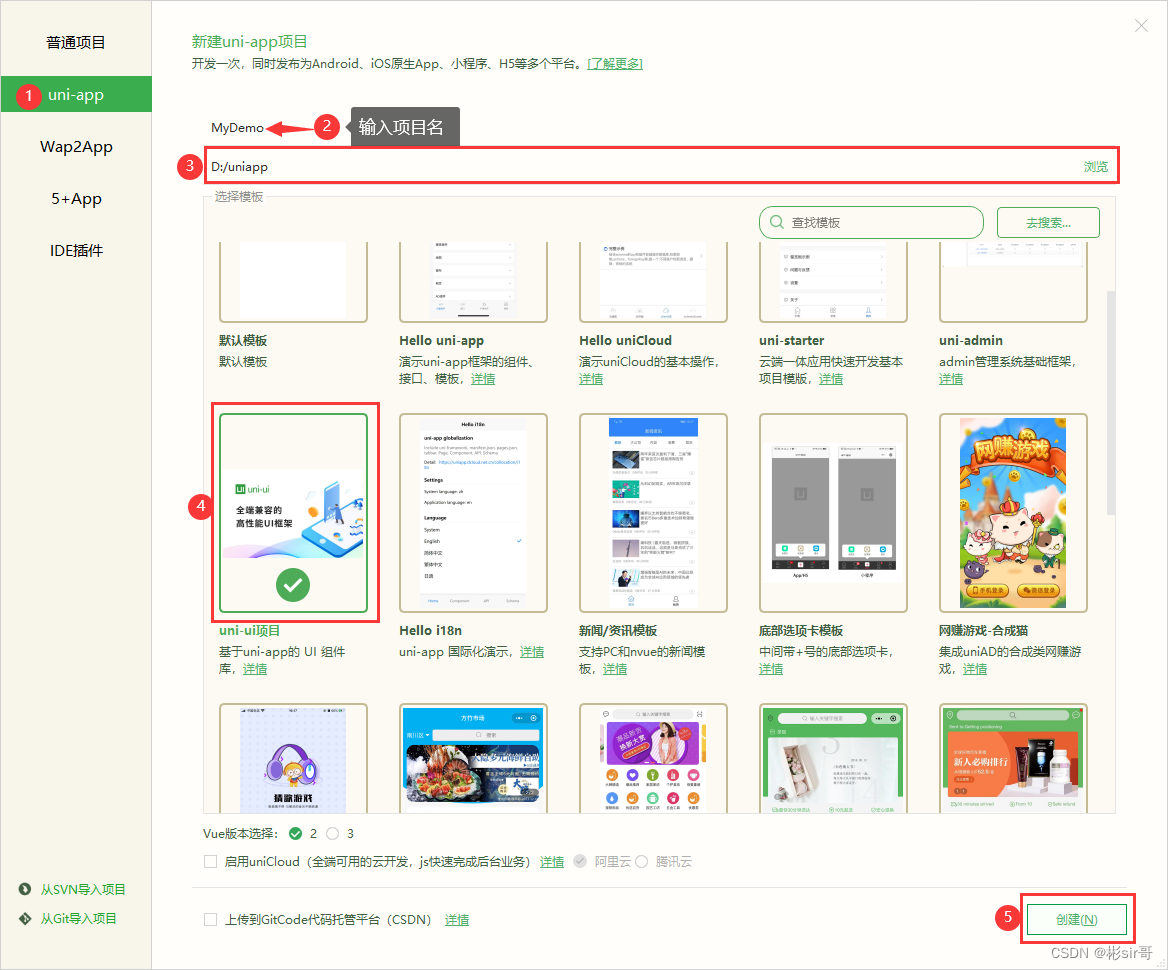
Download install and create/run project for HBuilderX
initramfs详解----添加硬盘驱动并访问磁盘
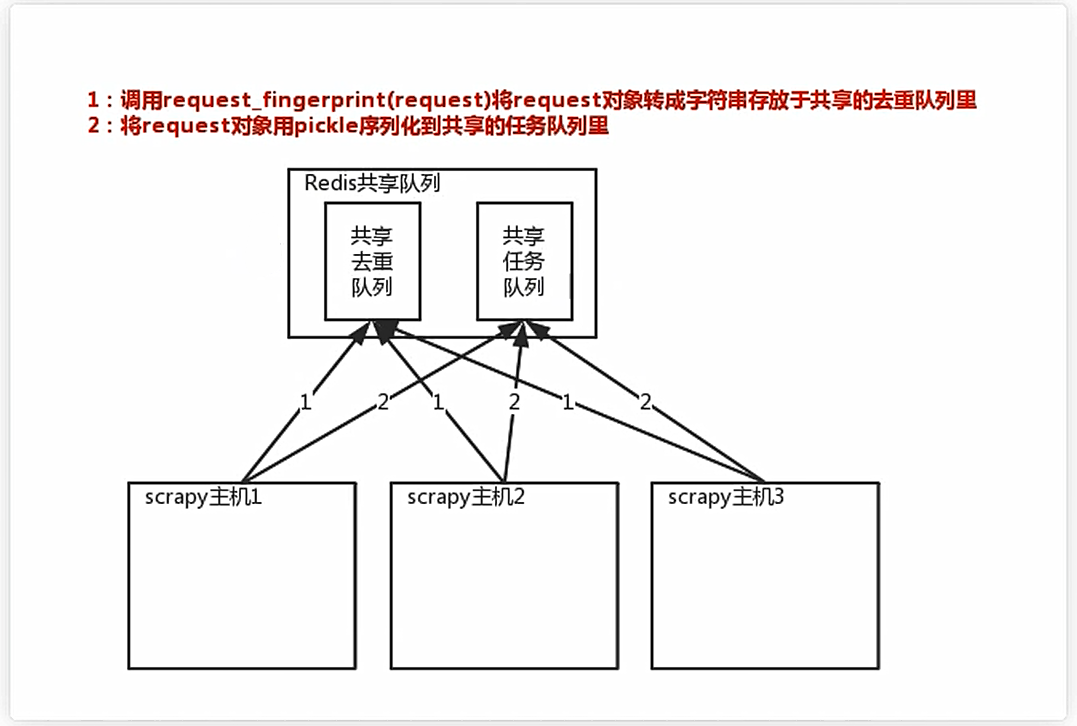
5. Scrapy middleware & distributed crawler

Kubernetes:(十一)KubeSphere的介绍和安装(华丽的篇章)

织梦内核电动伸缩门卷闸门门业公司网站模板 带手机版【站长亲测】
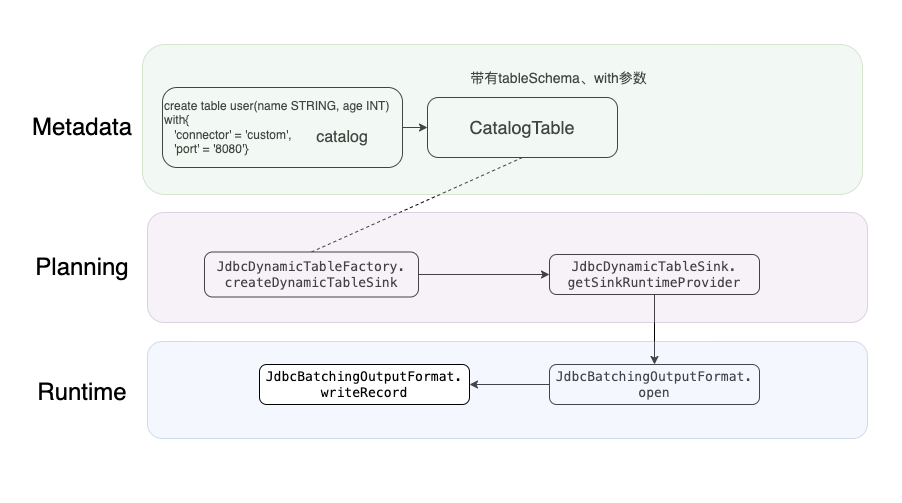
Flink jdbc connector 源码改造sink之 clickhouse多节点轮询写与性能分析

Example 037: Sorting

Security First: Tools You Need to Know to Implement DevSecOps Best Practices
随机推荐
静态/动态代理模式
Oracle迁移到瀚高之后,空值问题处理
splice随机添加和删除的写法
第13章 网络安全漏洞防护技术原理与应用
html select tag assignment database query result
Flask框架初学-05-命令管理Manager及数据库的使用
MallBook 助力SKT思珂特教育集团,立足变化,拥抱敏捷交易
实例040:逆序列表
nodejs installation and environment configuration
Continuing to pour money into commodities research and development, the ding-dong buy vegetables in win into the supply chain
halcon自定义函数基本操作
initramfs详解----添加硬盘驱动并访问磁盘
DDTL: Domain Transfer Learning at a Distance
参加Oracle OCP和MySQL OCP考试的学员怎样在VUE预约考试
Use of lombok annotation @RequiredArgsConstructor
Is there any jdbc link to Youxuan database documentation and examples?
The idea of the diagram
MallBook联合人民交通出版社,推动驾培领域新发展,开启驾培智慧交易新生态
织梦内核电动伸缩门卷闸门门业公司网站模板 带手机版【站长亲测】
Sticker Spelling - Memory Search / Shape Pressure DP