当前位置:网站首页>完美二叉树、完全二叉树、完满二叉树
完美二叉树、完全二叉树、完满二叉树
2022-06-29 09:10:00 【水似冰】
1、二叉树(Binary Tree)
1.1 什么是二叉树(Binary Tree)
每个结点至多拥有两棵子树(即二叉树中不存在度大于2的结点),并且,二叉树的子树有左右之分,其次序不能任意颠倒。
1.2 二叉树的性质
- 若二叉树的层次从0开始,则在二叉树的第i层至多有2^i个结点(i>=0)。
- 高度为k的二叉树最多有2^(k+1) - 1个结点(k>=-1)。 (空树的高度为-1)
- 对任何一棵二叉树,如果其叶子结点(度为0)数为m, 度为2的结点数为n, 则m = n + 1。
2、完美二叉树
一个深度为k(>=-1)且有2^(k+1) - 1个结点的二叉树称为完美二叉树
换句话说:树是满的,还是二叉的
图是这样的: 
3、完全二叉树(Complete)
完全二叉树从根结点到倒数第二层满足完美二叉树,最后一层可以不完全填充,其叶子结点都靠左对齐
下图就不是一棵完全(Complete)二叉树 
如果将编号11(K)结点从编号6(E)的左儿子位置移动到编号5(E)的右儿子位置,则变成一棵完全(Complete)二叉树。
- 其实,理解完全(Complete)二叉树可以借助于栈(stack)的思想。 例如,把第一个图中的完美(Perfect)二叉树的所有结点按照编号1, 2, 3, …, 15依次入栈(push)。 那么,对栈的每一次出栈(pop)操作后,栈里保存的结点集对应到图上去都是一棵完全(Complete)二叉树
4、完满二叉树
所有非叶子结点的度都是2
换句话说:只要你有孩子,你就必然是有两个孩子。
参考博客:
完美二叉树, 完全二叉树和完满二叉树
例:
一个具有767个节点的完全二叉树,其叶子节点的个数为____
A . 383
B . 384
C . 385
D . 386
n = n2+n1+no
n0 = n2 + 1
可得方程:n0= (768-n1) / 2,又因完全二叉数节点为1的数要不为1要不为0,故选B。
- n:总节点数
- n2:度为2的节点数
- n1:度为1的节点书
- n0:度为0节点数
边栏推荐
- How to do unit test well
- Data visualization: the significance of data visualization
- 长安链数据存储介绍及Mysql存储环境搭建
- MATLAB小技巧(21)矩阵分析--偏最小二乘回归
- MySQL modify auto increment initial value
- 官方stm32芯片包下载地址 stm32f10x stm32f40x下载
- How to set Google Chrome as the default browser
- 股票炒股账号开户安全吗?是靠谱的吗?
- [Huawei certification] the most complete and selected question bank in hcia-datacom history (with answer analysis)
- IDEA自动补全
猜你喜欢

Segmentation of Head and Neck Tumours Using Modified U-net
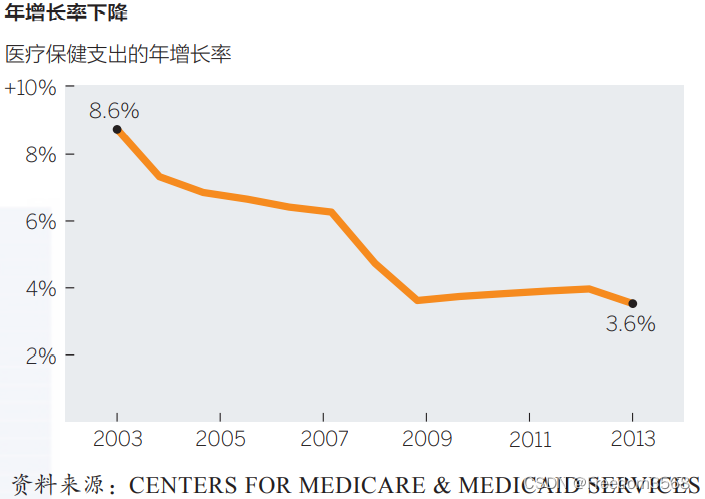
数据可视化:数据可视化四象限,教你正确应用图标

转载 :判断对象是否具有属性的5种方法

Do you know what BFD is? This article explains the principle and usage scenarios of BFD protocol in detail

Zabbix4.4 configure the indicators of the monitoring server and solve the garbled graphics pages

MySQL configuring master-slave databases

kdevelop新建工程
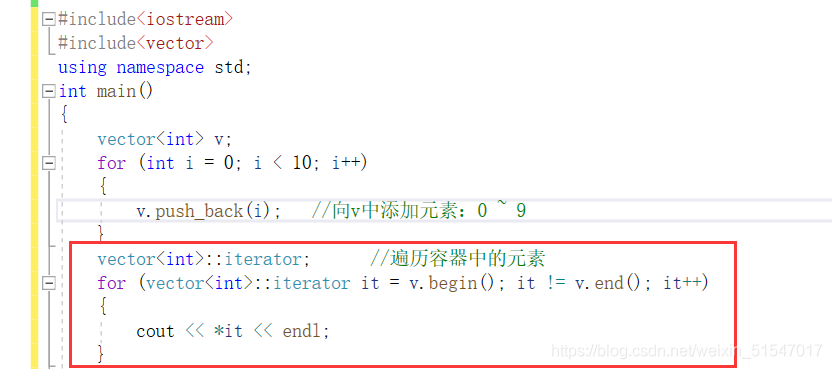
How to traverse objects in the vector container
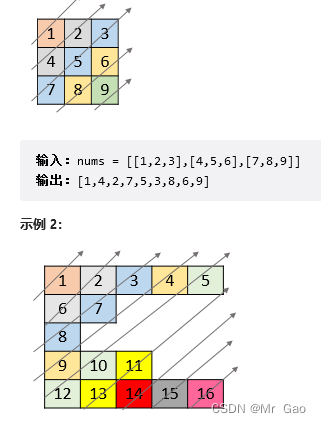
1424. 对角线遍历 II

Gd32f4xx Ethernet chip (ENC28J60) driver migration
随机推荐
Reading notes on how to connect the network - Web server request and response (V)
[noi Simulation Competition] add points for noi (heavy chain dissection, line segment tree)
Introduction to Chang'an chain data storage and construction of MySQL storage environment
Gd32f4xx Ethernet chip (ENC28J60) driver migration
Could not open JDBC connection for transaction
2020-09-29 非商品模板化代码层次 rapidjson库
Install and configure redis in the Linux environment, and set the boot auto start
Cloud management platform: 9 open source cloud management platforms (CMP)
LC236. 二叉树的最近公共祖先
IDEA调试失败,报JDWP No transports initialized, jvmtiError=AGENT_ERROR_TRANSPORT_LOAD(196)
The 23 most useful elasticsearch search techniques you must know
Deep Learning-based Automated Delineation of Head and Neck Malignant Lesions from PET Images
Zabbix4.4 configure the indicators of the monitoring server and solve the garbled graphics pages
Chang'an chain go language smart contract writing and compilation
数据源连接池未关闭的问题 Could not open JDBC Connection for transaction
InvalidConnectionAttributeException异常处理
A 3D Dual Path U-Net of Cancer Segmentation Based on MRI
阿里云服务器安装配置redis,无法远程访问
安装Anaconda后启动JupyterLab需要输入密码
Hystrix熔断器:服务熔断与服务降级
