【L1、L2、smooth L1三类损失函数】

---

一、常见的MSE、MAE损失函数

1.1 均方误差、平方损失

均方误差（MSE）是回归损失函数中最常用的误差，它是预测值与目标值之间差值的平方和，其公式如下所示：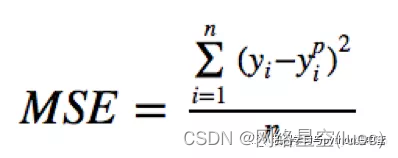

下图是均方根误差值的曲线分布，其中最小值为预测值为目标值的位置。

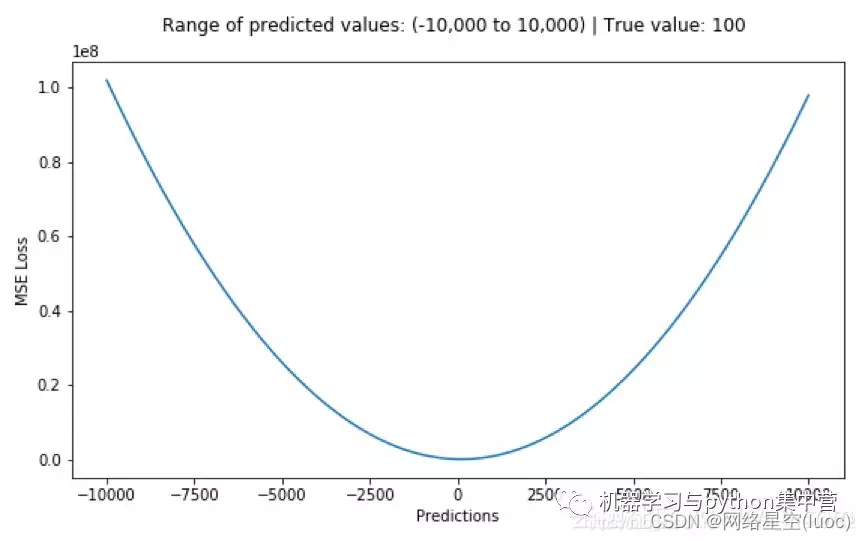
优点：各点都连续光滑，方便求导，具有较为稳定的解

缺点：不是特别的稳健，为什么？因为当函数的输入值距离中心值较远的时候，使用梯度下降法求解的时候梯度很大，可能导致梯度爆炸。

什么是梯度爆炸？
误差梯度是神经网络训练过程中计算的方向和数量，用于以正确的方向和合适的量更新网络权重。
在深层网络或循环神经网络中，误差梯度可在更新中累积，变成非常大的梯度，然后导致网络权重的大幅更新，并因此使网络变得不稳定。在极端情况下，权重的值变得非常大，以至于溢出，导致 NaN 值。
网络层之间的梯度（值大于 1.0）重复相乘导致的指数级增长会产生梯度爆炸。

梯度爆炸引发的问题
在深度多层感知机网络中，梯度爆炸会引起网络不稳定，最好的结果是无法从训练数据中学习，而最坏的结果是出现无法再更新的 NaN 权重值。

1.2 平均绝对误差

平均绝对误差（MAE）是另一种常用的回归损失函数， 它是目标值与预测值之差绝对值的和，表示了预测值的平均误差幅度，而不需要考虑误差的方向，范围是0到∞，其公式如下所示：

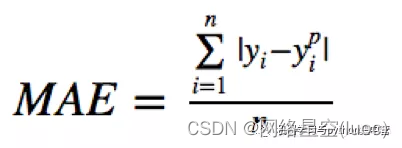
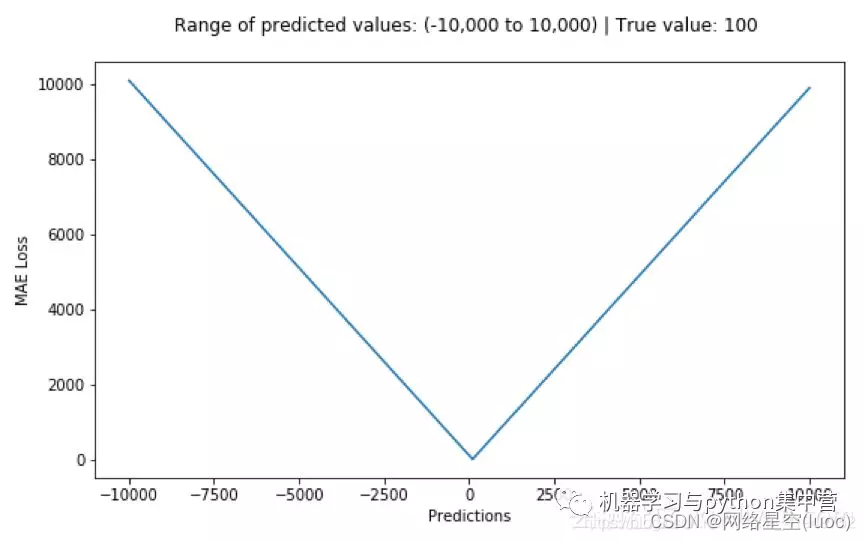
优点：无论对于什么样的输入值，都有着稳定的梯度，不会导致梯度爆炸问题，具有较为稳健性的解。

缺点：在中心点是折点，不能求导，不方便求解。

上面的两种损失函数也被称之为L2损失和L1损失。

二、L1_Loss和L2_Loss

2.1 L1_Loss和L2_Loss的公式

L1范数损失函数，也被称为最小绝对值偏差（LAD），最小绝对值误差（LAE）。 总的说来，它是把目标值（Yi)与估计值（f(xi))的绝对差值的总和（S)最小化：

L2范数损失函数，也被称为最小平方误差（LSE）。 总的来说，它是把目标值（Yi)与估计值（f(xi))的差值的平方和（S)最小化：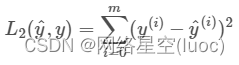

import numpy as np

def L1(yhat, y):
    loss = np.sum(np.abs(y - yhat))
    return loss

def L2(yhat, y):
    loss =np.sum(np.power((y - yhat), 2))
    return loss
#调用
yhat = np.array([0.1, 0.2, 0.3, 0.4, 0.5])
y = np.array([1, 1, 0, 1, 1])

print("L1 = " ,(L1(yhat,y)))
print("L2 = " ,(L2(yhat,y)))

L1范数与L2范数作为损失函数的区别能快速地总结如下：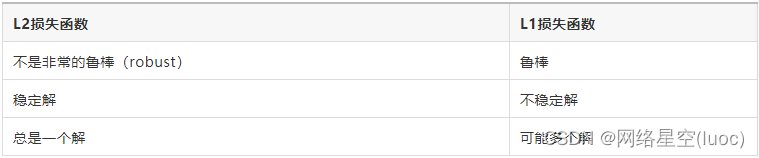

2.2 几个关键的概念

（1）鲁棒性
最小绝对值偏差之所以是鲁棒的，是因为它能处理数据中的异常值。这或许在那些异常值可能被安全地和有效地忽略的研究中很有用。如果需要考虑任一或全部的异常值，那么最小绝对值偏差是更好的选择。

从直观上说，因为L2范数将误差平方化（如果误差大于1，则误差会放大很多），模型的误差会比L1范数来得大，因此模型会对这个样本更加敏感，这就需要调整模型来最小化误差。如果这个样本是一个异常值，模型就需要调整以适应单个的异常值，这会牺牲许多其它正常的样本，因为这些正常样本的误差比这单个的异常值的误差小。

（2）稳定性
最小绝对值偏差方法的不稳定性意味着，对于数据集的一个小的水平方向的波动，回归线也许会跳跃很大（如，在转折点处求导）。在一些数据结构上，该方法有许多连续解；但是，对数据集的一个微小移动，就会跳过某个数据结构在一定区域内的许多连续解。在跳过这个区域内的解后，最小绝对值偏差线可能会比之前的线有更大的倾斜。

相反地，最小平方法的解是稳定的，因为对于一个数据点的任何微小波动，回归线总是只会发生轻微移动；也就说，回归参数是数据集的连续函数。

三、smooth L1损失函数

其实顾名思义，smooth L1说的是光滑之后的L1，前面说过了L1损失的缺点就是有折点，不光滑，导致不稳定，那如何让其变得光滑呢？smooth L1损失函数为：

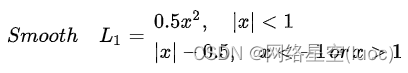
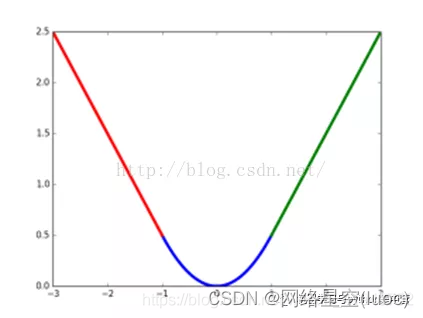
smooth L1损失函数曲线如下图所示，作者这样设置的目的是想让loss对于离群点更加鲁棒，相比于L2损失函数，其对离群点（指的是距离中心较远的点）、异常值（outlier）不敏感，可控制梯度的量级使训练时不容易跑飞。