当前位置:网站首页>Eigen User Guide (Introduction)
Eigen User Guide (Introduction)
2022-07-06 15:10:00 【naibula】
1 install Eigen
Eigen Source download :http://eigen.tuxfamily.org/index.php?title=Main_Page
It is recommended to download the latest stable version ,Windows Environment can be downloaded “zip” File format ,Linux Environment downloadable “tar.gz” File format . The following analysis will be based on Eigen3.3.7 For example , Introduce Eigen Installation .
chart 1-1 Eigen Website screenshot
1.1 Window10(64 position )+Visual Studio2017
Decompress the source code , Get a folder with a long name , Go to this folder , You can see the following file directory . In the following illustration ,Eigen Folder is the source file directory we need to use , Usually, you can use it as long as you copy the file to the corresponding project Eigen library . Get into Eigen Folder , You can see there's one Dense file , This is a header file interface , In the use of Eigen The header file needs to be included in the source code of the Library .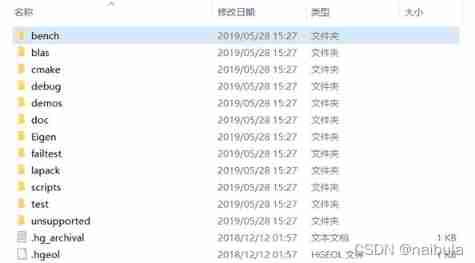
chart 1-2 Decompress the downloaded compressed package to get the directory 
chart 1-3 Eigen Source directory
Let's introduce Eigen How to use a simple use case , But the code is not explained here .
- open Visual Studio2017, Create a new one C++ project ( In turn, click file -> newly build -> project ), Form a good habit of setting the project path by yourself , Generally, the project is not built on C disc , Pictured 1-4;
- Enter the location of project storage , View project directory , be familiar with vs Create a directory structure , To create one called Eigen_Test Project as an example , The directory structure is shown in the figure 1-5 Shown ;
- stay vs2017 Add source files to , Name it main.cpp,main.cpp The contents in are appendices “source1.1”, The source code contains Dense file , This file is using Eigen Library interface ;
- Map 1-2 Medium Eigen Copy folder to figure 1-5Eigen_Test Under the solution directory , Pictured 1-6 Shown ;
- Compile operation , If you can compile and run normally , It means that Eigen The library has been successfully configured .
chart 1-4 Visual studio structure C++ engineering
chart 1-5 Visual studio Built project directory 
chart 1-6 Copy Eigen Project catalogue after
2 Eigen Use
stay Eigen, All matrices and vectors in are Matrix The object of the template class , A vector is just a special matrix .
2.1 Matrix class Matrix
Matrix Class has a total of six template parameters. First, only the first three parameters are introduced , The remaining three parameters have their default values . The three mandatory parameters are as follows :
Matrix<typename Scalar, int RowsAtCompileTime, int ColsAtCompileTime>
- Scalar yes scalar type , If you want to construct a single precision floating-point type matrix , You can choose float. All those who support Scalar Type see Scalar types.
- RowsAtCompileTime and ColsAtCompileTime It represents the number of rows and columns respectively , These two parameters are required to be known at compile time .
stay Eigen Macro definitions are provided in to easily access some commonly used types , Such as :
typedef Matrix<float, 4, 4> Matrix4f;
typedef Matrix<float, 3, 1> Vector3f;
typedef Matrix<int, 1, 2> RowVector2i;
Of course ,Eigen The library is not limited to those cases where the dimension of the matrix is known at compile time .RowsAtCompileTime and ColsAtCompileTime You can take a special value Dynamic, This means that the dimension of the matrix is unknown at compile time , Must be handled as a runtime variable . stay Eigen In terms of ,Dynamic Called dynamic size (dynamic size), The size known at runtime is called fixed size (fixed size).
Create a double precision dynamic matrix
typedef Matrix<double, Dynamic, Dynamic> MatrixXd;
Create an integer column vector
typedef Matrix<int, Dynamic, 1> VectorXi;
Matrix The other three template parameters of are selectable , The complete parameters are as follows :
Matrix<typename Scalar,
int RowsAtCompileTime,
int ColsAtCompileTime,
int Options = 0,
int MaxRowsAtCompileTime = RowsAtCompileTime,
int MaxColsAtCompileTime = ColsAtCompileTime>
- Options Is a bit field , Its value can only take RowMajor、ColMajor, Respectively, it means that rows are stored first 、 Column priority storage . By default, column first storage is used , In a general way Eigen The library is more efficient when columns are stored first .Eigen Specify the storage form of , It just affects the form of the matrix in memory , It will not affect the access habits of the matrix .
- MaxRowsAtCompileTime and MaxColsAtCompileTime Used to specify the maximum dimension of the matrix . Although sometimes I don't know the exact size of the matrix , But the upper bound of the matrix dimension is known at compile time , Then you can specify these two parameters to avoid dynamic memory allocation .
1.2.2 Matrix initialization and access
Eigen The library provides a default constructor , It does not provide dynamic memory allocation , Nor will it initialize the value of any matrix .Eigen Types can be used like this :
Matrix3f a;
MatrixXf b;
here
- a It's a 3*3 Matrix , The elements of the matrix are not initialized ;
- b Is a dynamic matrix , Its size is 0*0, That is, no memory has been allocated for this matrix .
Constructor provides overloads that specify the size of the matrix . For a matrix , The first parameter is the number of rows of the matrix . For vectors, you only need to specify the size of the vector . It allocates the amount of memory needed by the matrix or vector , But their values are not initialized .
MatrixXf a(10,15);
VectorXf b(30);
- a It's a 10*15 Dynamic matrix of , Memory is allocated , But not initialized ;
- b It's a size of 30 Dynamic array of , But not initialized .
Eigen Library overloaded parentheses () Access the elements of a matrix or vector , The serial number from 0 Start .Eigen The library does not support the use of square brackets [] Access the elements of the matrix ( Except vector ).
MatrixXd m(2,2);
m(0,0) = 3;
VectorXd v(2);
v(0) = 4;
Comma expression initialization
Matrix3f m;
m << 1, 2, 3,
4, 5, 6,
7, 8, 9;
std::cout << m;
have access to rows()、cols()、size() Access the current size of the matrix , Use resize() Reset the size of the matrix . If the size of the matrix does not change , that resize() The operation has no effect . If the size of the matrix changes , Then the value of the matrix may change . If you want to resize without changing the value of the matrix, use conservativeResize().
Use the assignment operator “=”,Eigen Reset the size of the left operand to the size of the right operand .
2.3 Matrix and vector algebra
Addition and subtraction : heavy load C++ in “+”、“-”、“+=”、“-=” The operator , The dimensions of the left and right operands are required to be the same . It is not allowed to add or subtract a number from a vector .
Number multiplication and number division : heavy load C++ in “”、“/”、“=”、“/=” The operator , Support matrix and vector multiply or divide by a number .
Transpose and conjugate : Transposition aT、 conjugate 、 Conjugate transpose aH Pass respectively transpose()、conjugate()、adjoint() Realization . Invocation format a.transpose(),a.conjugate(),a.adjoint(). For real numbers , Conjugation has no effect , Conjugate transpose is equivalent to transpose . Use a = a.transpose() There may be mistakes , This is because Eigen When transposing or conjugating , Write the left operand at the same time , So as to get unexpected results . To realize this function, you can use a.transposeInPlace(). Allied , Also support adjointInPlace().
matrix - Matrix and matrix - Vector multiplication : Because in Eigen The medium vector is just a special matrix , So just reload “*”、“*=” You can realize the multiplication of matrix and vector . If you're worried m=mm Will cause confusion , Now you can dispel this doubt , because Eigen Deal with matrix multiplication in a special way , compile m=mm when , As
tmp = m*m;
m = tmp;
Dot product and cross product : Dot product can also be called inner product ,Eigen Separate use dot() and cross() To realize inner product and vector product . Cross multiplication is only applicable to three-dimensional vectors .
Vector3d v(1,2,3);
Vector3d w(0,1,2);
v.dot(w);
v.cross(w);
Basic algebraic calculation :mat.sum() Calculate the sum of all matrix elements ,mat.pro() Calculate the continuous product of all elements ,mat.mean() Calculate the average of all elements ,mat.minCoeff() Calculate the minimum value of matrix elements ,mat.maxCoeff Calculate the maximum value of matrix elements ,mat.trace() Calculate the trace of the matrix . Functions that calculate the maximum and minimum values support returning the positions of the maximum and minimum values :
Matrix3f m = Matrix3f::Random();
std::ptrdiff_t i, j; //ptrdiff_t yes stddef.h The data type used to represent the interval between two pointers in , It's symbolic
float minOfM = m.minCoeff(&i,&j);
Be careful :
- In the calculation process, if the matrix dimension does not meet the corresponding conditions , that Eigen The library can check the contradiction of static matrix dimension at compile time , There are corresponding dynamic inspection methods for dynamic matrix , If there are dimensional contradictions, the program may crash .
- None of the above operations will affect the operand itself .
- adopt “.” The operation called by the operator can be used as an lvalue , Of course, this doesn't make much sense in general .
2.4 Array class Array
Array Class provides arrays in the usual sense , It provides some convenient nonlinear operations on elements . For example, add a constant to all elements , Or let two Arrays The value of corresponds to multiply .
Array Class template and Matrix be similar , See Matrix Class introduction .Array In its storage form, it has the form of matrix , Just say Array Supported operations and Matrix Dissimilarity .
Array<typename Scalar, int RowsAtCompileTime, int ColsAtCompileTime>;
Array<float,Dynamic,1> ArrayXf;
Array<float,3,1> Array3f;
Array<double,Dynamic,Dynamic> ArrayXXd;
visit Array And Matrix It's the same . The following describes and Matrix Different operation :
Add, subtract, multiply and divide : Add the corresponding position elements ( reduce 、 ride 、 except ).
ArrayXXf a(2,2);
ArrayXXf b(2,2);
a << 1,2,3,4;
b << 5,6,7,8;
cout<<a*b;
The output is :
5 12
21 32
square root 、 The absolute value : By calling sqrt()、abs() function ,a.abs().
Find the minimum value of two matrices :a.min(b), requirement a and b The dimensions of are the same , Find the minimum value of the two numbers at the corresponding position .
Eigen The supported array element operations are shown in Figure 2-1 Shown . that , How to choose Matrix and Array Well ? If you want to support the operation of linear algebra , Just choose Matrix; If you want to do coefficient-wise operation , Just choose Array. If you want to support linear algebra operations , And to support coefficient-wise operation , Then you can use it .array() and .matrix() Implement type conversion , This conversion has no computational cost . These operations will not change the matrix or array that calls the function itself, but return a copy .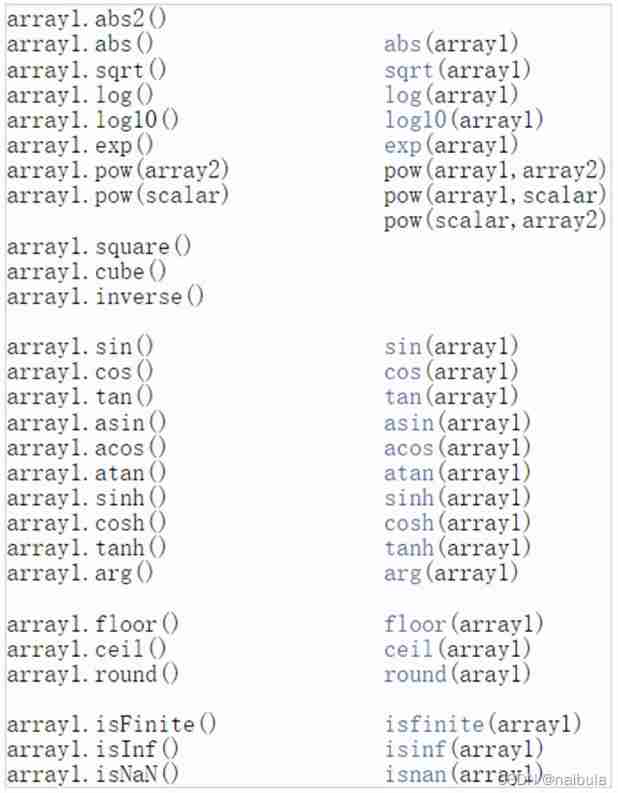
chart 2-1 Eigen Supported array meta operations
2.5 Block operation
A block is a rectangular region of a matrix , Block expressions can be left-hand or right-hand . The most common is block() operation , It has two versions :
matrix.block(i,j,p,q);// Dynamically sized blocks
matrix.block<p,q>(i,j);// Fixed size blocks
i、j Indicates the starting position of the block ( The angular sign of the upper left corner element of the block in the matrix ),p、q Represents the size of the block . Fixed size blocks are more efficient at runtime .
Eigen::MatrixXf m(4,4);
m << 1, 2, 3, 4,
5, 6, 7, 8,
9,10,11,12,
13,14,15,16;
cout << m.block(0,0,i,i) << endl;
result :
Block of size 3x3
1 2 3
5 6 7
9 10 11
block() The operation can also be used for lvalues :
MatrixXd m(3,3);
VectorXd v(3);
m << 1, 2, 3,
4, 5, 6,
7, 8, 9;
v << 11, 12, 13;
m.block(0, 0, 3, 1) = v;
cout << m.block(0,0,3,1) << endl;
result :
11
12
13
block() Operations support arbitrary block operations , For some special visits Eigen Also provided API.
Block operation Method
ith row * matrix.row(i);
jth column * matrix.col(j);
alike ,row() Operation and col () The operation can be either an lvalue or an lvalue . besides ,Eigen It also provides shortcuts to access blocks in special locations , Pictured 1-8 Shown .
For vectors or one-dimensional arrays ,Eigen Special block operations are also provided , Pictured 1-9 Shown . These block operations are also available in static and dynamic versions .v.head(n) You can access the head of the vector n Elements ,v.tail(n) You can access the tail of the vector n Elements ,v.segment(i,j) You can access from the label i At the beginning j Elements .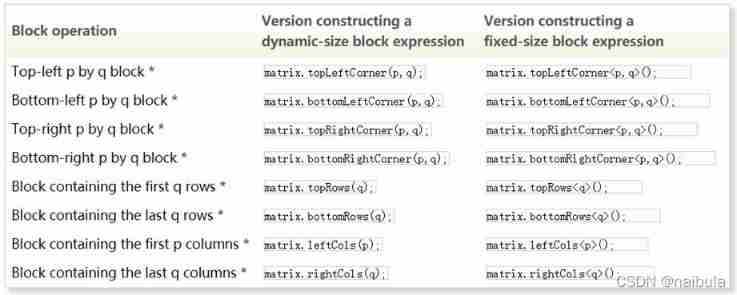
chart 1-8 Eigen Convenient operation of supported blocks
2.6 Library function
Random vector or matrix generation
Use Random function , Generate double precision random numbers in -1 To 1 Between , The random number that generates an integer is related to the machine from a negative integer to a positive integer . Examples :
MatrixXd m=MatrixXd::Random(2,3);
VectorXi v= VectorXi::Random(1);
Zero vector or matrix generation
Use Zero() function , Generate a matrix or vector with all zero values .
MatrixXd m=MatrixXd::Zero(2,3);
VectorXi v= VectorXi::Zero(1);
Generate unit matrix
Use Identity() function , Generate identity matrix or quasi identity matrix .
MatrixXd m= MatrixXd::Identity(5,5);
MatrixXd m= MatrixXd::Identity(5,4);
边栏推荐
- “Hello IC World”
- HackTheBox-Emdee five for life
- 全网最详细的postman接口测试教程,一篇文章满足你
- Face and eye recognition based on OpenCV's own model
- Opencv recognition of face in image
- Iterators and generators
- ucore lab8 文件系统 实验报告
- Want to learn how to get started and learn software testing? I'll give you a good chat today
- [pointer] the array is stored in reverse order and output
- UCORE lab7 synchronous mutual exclusion experiment report
猜你喜欢
In Oracle, start with connect by prior recursive query is used to query multi-level subordinate employees.
MySQL development - advanced query - take a good look at how it suits you

如何成为一个好的软件测试员?绝大多数人都不知道的秘密
CSAPP homework answers chapter 789

The minimum number of operations to convert strings in leetcode simple problem
软件测试面试要问的性能测试术语你知道吗?
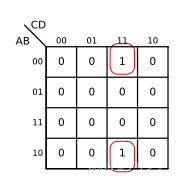
数字电路基础(二)逻辑代数

The minimum sum of the last four digits of the split digit of leetcode simple problem
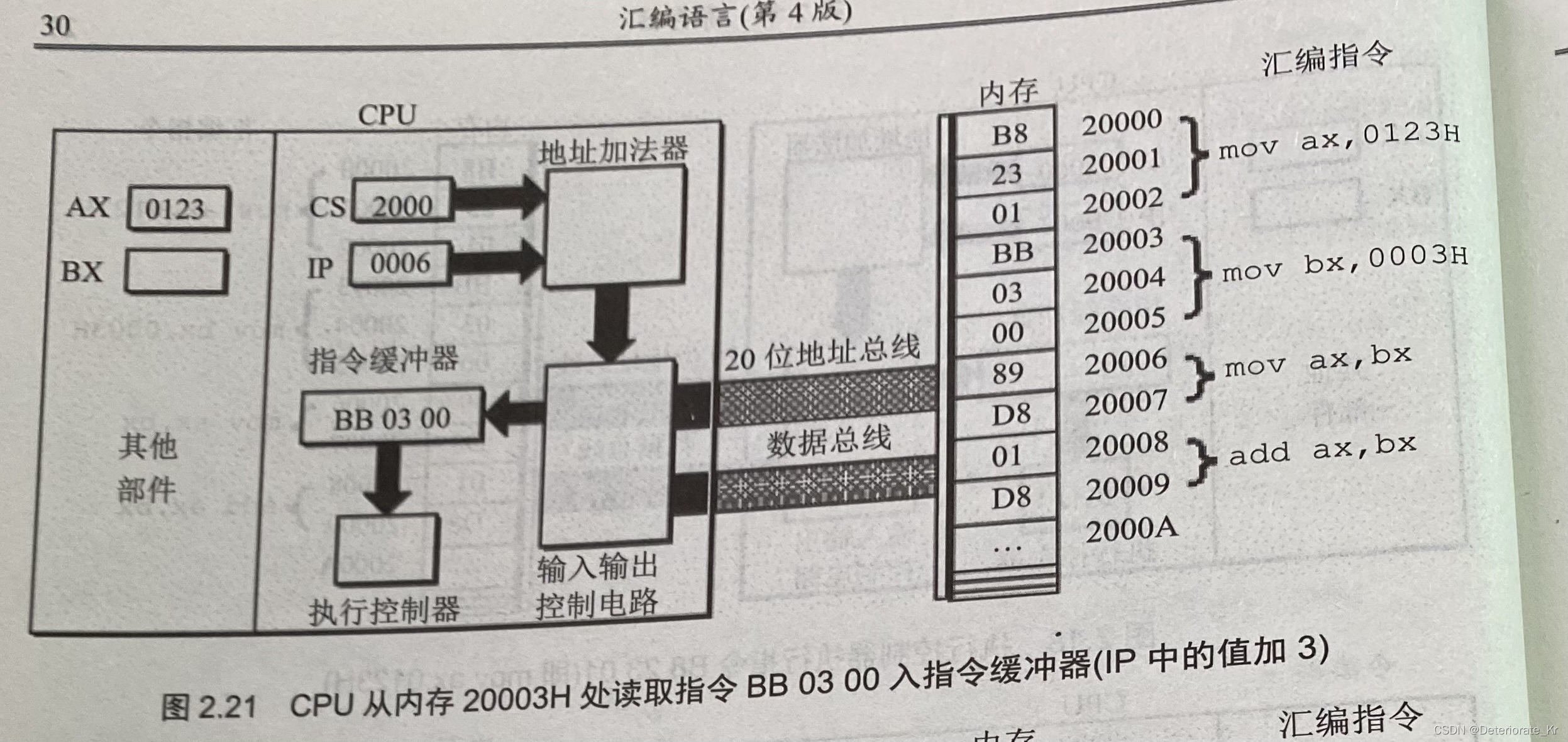
Wang Shuang's detailed learning notes of assembly language II: registers
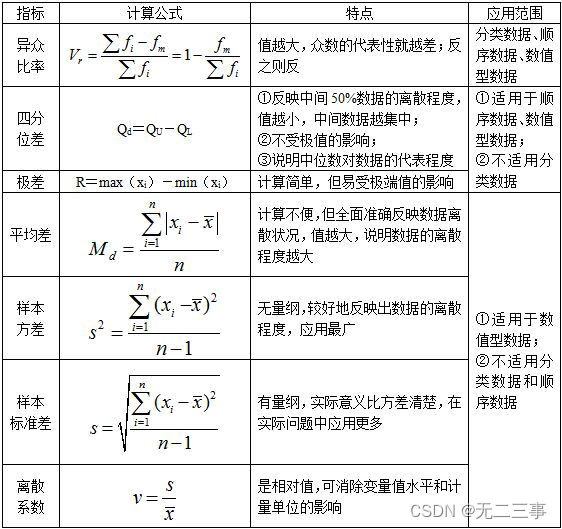
Statistics 8th Edition Jia Junping Chapter 4 Summary and after class exercise answers
随机推荐
Investment should be calm
Stc-b learning board buzzer plays music 2.0
C language learning summary (I) (under update)
Collection集合与Map集合
Daily code 300 lines learning notes day 9
Global and Chinese markets for complex programmable logic devices 2022-2028: Research Report on technology, participants, trends, market size and share
接口测试面试题及参考答案,轻松拿捏面试官
What is an index in MySQL? What kinds of indexes are commonly used? Under what circumstances will the index fail?
Want to learn how to get started and learn software testing? I'll give you a good chat today
CSAPP homework answers chapter 789
软件测试面试要问的性能测试术语你知道吗?
[oiclass] share prizes
Global and Chinese market for antiviral coatings 2022-2028: Research Report on technology, participants, trends, market size and share
[pointer] delete all spaces in the string s
"If life is just like the first sight" -- risc-v
后台登录系统,JDBC连接数据库,做小案例练习
UCORE lab1 system software startup process experimental report
CSAPP家庭作業答案7 8 9章
Global and Chinese markets of electronic grade hexafluorobutadiene (C4F6) 2022-2028: Research Report on technology, participants, trends, market size and share
Stc-b learning board buzzer plays music
