当前位置:网站首页>Hands on deep learning (37) -- cyclic neural network
Hands on deep learning (37) -- cyclic neural network
2022-07-04 09:40:00 【Stay a little star】
List of articles
Cyclic neural network
In the language model , We introduced n n n Metagrammar model , Words in it x t x_t xt In time step t t t The conditional probability of depends only on the previous n − 1 n-1 n−1 Word . If we want to take time step t − ( n − 1 ) t-(n-1) t−(n−1) The possible effects of previous words are merged into x t x_t xt On , We need to increase n n n. however , The number of model parameters will also increase exponentially , Because we need a vocabulary V \mathcal{V} V Storage ∣ V ∣ n |\mathcal{V}|^n ∣V∣n A digital . therefore , Its modeling P ( x t ∣ x t − 1 , … , x t − n + 1 ) P(x_t \mid x_{t-1}, \ldots, x_{t-n+1}) P(xt∣xt−1,…,xt−n+1), It's better to use the implicit variable model :
P ( x t ∣ x t − 1 , … , x 1 ) ≈ P ( x t ∣ h t − 1 ) , P(x_t \mid x_{t-1}, \ldots, x_1) \approx P(x_t \mid h_{t-1}), P(xt∣xt−1,…,x1)≈P(xt∣ht−1),
among h t − 1 h_{t-1} ht−1 yes Hidden state ( Also known as hidden variables ), It stores time steps t − 1 t-1 t−1 The sequence information of . Usually , Can be based on current input x t x_{t} xt And previously hidden h t − 1 h_{t-1} ht−1 To calculate the time step t t t Hidden state at any time :
h t = f ( x t , h t − 1 ) . h_t = f(x_{t}, h_{t-1}). ht=f(xt,ht−1).
For functions that are powerful enough f f f, The implicit variable model is not an approximation . After all , h t h_t ht It may just store all the data observed so far . However , It may make computing and storage expensive .
For neural networks , It is worth noting that hidden layer and hidden state refer to two distinct concepts :
- Hidden layers are layers hidden from the view on the path from input to output .
- Technically speaking , Hidden state is the result of everything we do in a given step “ Input ”. The hidden status can only be calculated by viewing the data of the previous time point .
Cyclic neural network (Recurrent neural networks, RNNs) It is a neural network with hidden state . Introducing RNN Before the model , We first review the multilayer perceptron model .
One 、 Neural network without hidden state
Let's take a look at a multi-layer perceptron with only a single hidden layer . Let the activation function of the hidden layer be ϕ \phi ϕ. Given a small batch of samples X ∈ R n × d \mathbf{X} \in \mathbb{R}^{n \times d} X∈Rn×d, The batch size is n n n, Input is d d d dimension . Hidden layer output H ∈ R n × h \mathbf{H} \in \mathbb{R}^{n \times h} H∈Rn×h Calculate by the following formula :
H = ϕ ( X W x h + b h ) . \mathbf{H} = \phi(\mathbf{X} \mathbf{W}_{xh} + \mathbf{b}_h). H=ϕ(XWxh+bh).
In the above formula , We have weight parameters for hidden layers W x h ∈ R d × h \mathbf{W}_{xh} \in \mathbb{R}^{d \times h} Wxh∈Rd×h、 Offset parameters b h ∈ R 1 × h \mathbf{b}_h \in \mathbb{R}^{1 \times h} bh∈R1×h, The number of hidden cells is h h h. therefore , Apply broadcast mechanism during summation . Next , The variable will be hidden H \mathbf{H} H Used as input to the output layer . The output layer is given by the following formula :
O = H W h q + b q , \mathbf{O} = \mathbf{H} \mathbf{W}_{hq} + \mathbf{b}_q, O=HWhq+bq,
among , O ∈ R n × q \mathbf{O} \in \mathbb{R}^{n \times q} O∈Rn×q It's the output variable , W h q ∈ R h × q \mathbf{W}_{hq} \in \mathbb{R}^{h \times q} Whq∈Rh×q It's a weight parameter , b q ∈ R 1 × q \mathbf{b}_q \in \mathbb{R}^{1 \times q} bq∈R1×q Is the offset parameter of the output layer . If it's a classification problem , We can use softmax ( O ) \text{softmax}(\mathbf{O}) softmax(O) To calculate the probability distribution of the output category .
This is completely similar to the regression problem we solved in the sequence model , So we omit the details . so to speak , We can randomly select features - Label pair , And through automatic differentiation and random gradient descent to learn network parameters .
Two 、 Cyclic neural networks with hidden states
When we have a hidden state , It's totally different . Let's look at this structure in more detail .
Let's say we're in the time step t t t There are small batch inputs X t ∈ R n × d \mathbf{X}_t \in \mathbb{R}^{n \times d} Xt∈Rn×d. In other words , about n n n A small batch of sequence samples , X t \mathbf{X}_t Xt Each line of corresponds to a time step from the sequence t t t A sample at . Next , use H t ∈ R n × h \mathbf{H}_t \in \mathbb{R}^{n \times h} Ht∈Rn×h Time step t t t Hidden variables . Unlike the maximum likelihood algorithm , Here we save the hidden variables of the previous time step H t − 1 \mathbf{H}_{t-1} Ht−1, A new weight parameter is introduced W h h ∈ R h × h \mathbf{W}_{hh} \in \mathbb{R}^{h \times h} Whh∈Rh×h To describe how to use the hidden variables of the previous time step in the current time step . In particular , The hidden variable calculation of the current time step is determined by the input of the current time step and the hidden variable of the previous time step :
H t = ϕ ( X t W x h + H t − 1 W h h + b h ) . \mathbf{H}_t = \phi(\mathbf{X}_t \mathbf{W}_{xh} + \mathbf{H}_{t-1} \mathbf{W}_{hh} + \mathbf{b}_h). Ht=ϕ(XtWxh+Ht−1Whh+bh).
Compared with the cyclic neural network without hidden state , One more item is added to the above formula H t − 1 W h h \mathbf{H}_{t-1} \mathbf{W}_{hh} Ht−1Whh, Thus instantiating h t = f ( x t , h t − 1 ) h_t = f(x_t,h_{t-1}) ht=f(xt,ht−1). Hidden variables from adjacent time steps H t \mathbf{H}_t Ht and H t − 1 \mathbf{H}_{t-1} Ht−1 The relationship between them is known , These variables capture and retain the historical information of the sequence up to its current time step , Just like the state or memory of the current time step of neural network . therefore , Such hidden variables are called “ Hidden state ”(hidden state). Because the hidden state uses the same definition as the previous time step in the current time step , So the calculation is Cyclic (recurrent). therefore , The hidden state neural network based on cyclic computation is named Cyclic neural network (recurrent neural networks). The layer that performs output calculations in a recurrent neural network is called “ Circulation layer ”(recurrent layers).
There are many different ways to construct Recurrent Neural Networks . Recurrent neural networks with hidden states defined by the above formula are very common . For time steps t t t, The output of the output layer is similar to the calculation in multi-layer perceptron :
O t = H t W h q + b q . \mathbf{O}_t = \mathbf{H}_t \mathbf{W}_{hq} + \mathbf{b}_q. Ot=HtWhq+bq.
The parameters of the recurrent neural network include the weight of the hidden layer W x h ∈ R d × h , W h h ∈ R h × h \mathbf{W}_{xh} \in \mathbb{R}^{d \times h}, \mathbf{W}_{hh} \in \mathbb{R}^{h \times h} Wxh∈Rd×h,Whh∈Rh×h And offset b h ∈ R 1 × h \mathbf{b}_h \in \mathbb{R}^{1 \times h} bh∈R1×h, And the weight of the output layer W h q ∈ R h × q \mathbf{W}_{hq} \in \mathbb{R}^{h \times q} Whq∈Rh×q And offset b q ∈ R 1 × q \mathbf{b}_q \in \mathbb{R}^{1 \times q} bq∈R1×q. It is worth mentioning that , Even at different time steps , Recurrent neural networks always use these model parameters . therefore , The parameter cost of recurrent neural network will not increase with the increase of time step .
The following figure shows the computational logic of the recurrent neural network in three adjacent time steps . At any time step t t t, The calculation of hidden state can be regarded as :
- Set the current time step t t t The input of X t \mathbf{X}_t Xt And the previous time step t − 1 t-1 t−1 The hidden state of H t − 1 \mathbf{H}_{t-1} Ht−1 Link ;
- Send the link result to the activation function ϕ \phi ϕ The full connection layer of . The output of the full connection layer is the current time step t t t The hidden state of H t \mathbf{H}_t Ht.
In this case , The model parameters are W x h \mathbf{W}_{xh} Wxh and W h h \mathbf{W}_{hh} Whh The link to , as well as b h \mathbf{b}_h bh The offset of . Current time step t t t、 H t \mathbf{H}_t Ht The hidden state of will participate in the calculation of the next time step t + 1 t+1 t+1 The hidden state of H t + 1 \mathbf{H}_{t+1} Ht+1. Besides , Will also H t \mathbf{H}_t Ht Into the fully connected output layer , To calculate the current time step t t t Output O t \mathbf{O}_t Ot.

In fact, it's quite simple , Write here :
X t W x h + H t − 1 W h h = [ X t H t − 1 ] [ W x h W h h ] X_tW_{xh} + H_{t-1}W_{hh} = \begin{bmatrix} X_t & H_{t-1} \end{bmatrix} \begin{bmatrix} W_{xh}\\ W_{hh} \end{bmatrix} XtWxh+Ht−1Whh=[XtHt−1][WxhWhh]
Although this can be proved mathematically , But below we will only use a simple code snippet to illustrate this . First , We define the matrix X、W_xh、H and W_hh, Their shapes are (3,1)、(1,4)、(3,4) and (4,4). Separately X multiply W_xh, take H multiply W_hh, Then add the two multiplications , We get a shape of (3,4) Matrix .
import torch
from d2l import torch as d2l
X, W_xh = torch.normal(0, 1, (3, 1)), torch.normal(0, 1, (1, 4))
H, W_hh = torch.normal(0, 1, (3, 4)), torch.normal(0, 1, (4, 4))
torch.matmul(X, W_xh) + torch.matmul(H, W_hh)
tensor([[ 2.3381, -3.0454, 1.0498, 2.0654],
[ 2.1281, 6.2845, 0.9586, 0.6588],
[-2.1097, 1.7296, -1.0643, -1.9253]])
Now? , Let's go along the line ( Axis 1) Link matrix X and H, Along the line ( Axis 0) Link matrix W_xh and W_hh. These two links produce shapes respectively (3, 5) And shape (5, 4) Matrix . Multiply these two connected matrices , We get the same shape as above (3, 4) The output matrix of .
torch.matmul(torch.cat((X, H), 1), torch.cat((W_xh, W_hh), 0))
tensor([[ 2.3381, -3.0454, 1.0498, 2.0654],
[ 2.1281, 6.2845, 0.9586, 0.6588],
[-2.1097, 1.7296, -1.0643, -1.9253]])
3、 ... and 、 Character level language model based on recurrent neural network
Think about it , For the language model , Our goal is to predict the next marker based on current and past markers , So we shift the original sequence by a tag .Bengio wait forsomeone (Bengio.Ducharme.Vincent.ea.2003) First of all, it is proposed to use neural network for language modeling .
Next , We will show how to use recurrent neural networks to build language models . Set the small batch size to 1, The text sequence is "machine". In order to simplify the training of the subsequent part , We mark text as characters instead of words , And consider using Character level language model (character-level language model). The following figure shows how to use a cyclic neural network for character level language modeling , Predict the next character based on the current character and the previous character .

In the process of training , We analyze the output of the output layer of each time step softmax operation , Then the cross entropy loss is used to calculate the error between the model output and the label . Due to the cyclic calculation of the hidden state in the hidden layer , The time steps in the figure 3 Output O 3 \mathbf{O}_3 O3 By text sequence “m”、“a” and “c” determine . Because the next character of the sequence in the training data is “h”, So time step 3 The loss of will depend on the feature sequence based on this time step “m”、“a”、“c” Generate the next character probability distribution and label “h”.
actually , Each tag consists of a d d d The dimension vector represents , We use batch size n > 1 n>1 n>1. therefore , Input X t \mathbf X_t Xt In time step t t t It will be n × d n\times d n×d matrix .
Four 、 Confusion (Perplexity)—— Measuring the quality of language models
Last , Let's discuss how to measure the quality of language models , This will be used in the following part to evaluate our model based on recurrent neural network . One way is to check how surprising the text is . A good language model can predict what we will see next with high-precision tags . Consider different language models for phrases "It is raining" Propose the following Continuation :
- “It is raining outside”
- “It is raining banana tree”
- “It is raining piouw;kcj pwepoiut”
In terms of quality , example 1 Obviously the best . These words are wise , Logically, it is coherent . Although this model may not accurately reflect which word follows semantically (“in San Francisco” and “in winter” It may be a completely reasonable extension ), But the model can capture what kind of words follow . example 2 Produced a meaningless sequel , This is much worse . For all that , At least the model has learned how to spell words and some degree of correlation between words . Last , example 3 It is pointed out that the model with insufficient training cannot fit the data well .
We can measure the quality of the model by calculating the likelihood probability of the sequence . Unfortunately , This is a difficult number to understand and compare . After all , Shorter sequences are more likely to occur than longer sequences , So in Tolstoy's masterpiece 《 War and Peace 》 Evaluate the model on , Inevitably, it will be better than the novella of St. Exupery 《 The little prince 》 It is much less likely to happen . What is missing is equivalent to the average . Information theory comes in handy here . We are introducing softmax Entropy is defined in regression 、 Singular entropy and cross entropy , And in Online appendix of information theory More information theory is discussed in . If we want to compress the text , We can ask to predict the next tag given the current tag set . A better language model should allow us to predict the next tag more accurately . therefore , It should allow us to spend less bits when compressing sequences . So we can Through all in a sequence n n n The average cross entropy loss of markers :
1 n ∑ t = 1 n − log P ( x t ∣ x t − 1 , … , x 1 ) , \frac{1}{n} \sum_{t=1}^n -\log P(x_t \mid x_{t-1}, \ldots, x_1), n1t=1∑n−logP(xt∣xt−1,…,x1),
among P P P Given by language model , x t x_t xt It's in the time step t t t The actual marker observed from this sequence . This makes the performance on documents of different lengths comparable . For historical reasons , Natural language processing Scientists prefer to use a tool called “ Confusion ”(perplexity) The amount of . In short , It is the exponent of the above formula :
exp ( − 1 n ∑ t = 1 n log P ( x t ∣ x t − 1 , … , x 1 ) ) . \exp\left(-\frac{1}{n} \sum_{t=1}^n \log P(x_t \mid x_{t-1}, \ldots, x_1)\right). exp(−n1t=1∑nlogP(xt∣xt−1,…,x1)).
Confusion can best be understood as when we decide which tag to choose next , Harmonic mean of the actual number of choices . Let's take a look at some cases :
- In the best of circumstances , The model always perfectly estimates the probability of label marking as 1. under these circumstances , The confusion degree of the model is 1. ( Confusion =1 The sign prediction effect is good )
- In the worst case , The model always predicts that the probability of label marking is 0. under these circumstances , The degree of confusion is positive infinity .
- At baseline , The model predicts the uniform distribution of all available tags in the vocabulary . under these circumstances , The degree of confusion is equal to the number of unique marks in the vocabulary . in fact , If we store the sequence without any compression , This will be the best coding we can do . therefore , This provides an important upper limit , Any actual model must exceed this upper limit .
In the next few sections , We will implement recurrent neural networks for character level language models , And use confusion to evaluate these models .
Summary
- Neural networks that use cyclic computation for hidden states are called cyclic Neural Networks (RNN).
- The hidden state of the recurrent neural network can capture the historical information of the sequence up to the current time step .
- The number of parameters of the recurrent neural network model will not increase with the increase of time steps .
- We can use recurrent neural networks to create character level language models .
- We can use the degree of confusion to evaluate the quality of language models .
practice
- If we use a recurrent neural network to predict the next character in the text sequence , So what is the dimension required for any output ?
Enter the latitude
- Why can the recurrent neural network represent the conditional probability of the tag at a certain time step based on all the previous tags in the text sequence ?
Each layer will use the previous hidden state
- If you back propagate a long sequence , What happens to the gradient ?
Gradient explosion or disappearance ( The step is too long )
- What are the problems related to the language model described in this section ?
边栏推荐
- How does idea withdraw code from remote push
- Reload CUDA and cudnn (for tensorflow and pytorch) [personal sorting summary]
- Global and Chinese markets of water heaters in Saudi Arabia 2022-2028: Research Report on technology, participants, trends, market size and share
- SSM online examination system source code, database using mysql, online examination system, fully functional, randomly generated question bank, supporting a variety of question types, students, teache
- QTreeView+自定义Model实现示例
- Summary of the most comprehensive CTF web question ideas (updating)
- Leetcode (Sword finger offer) - 35 Replication of complex linked list
- "How to connect the Internet" reading notes - FTTH
- Are there any principal guaranteed financial products in 2022?
- Write a jison parser from scratch (1/10):jison, not JSON
猜你喜欢

2022-2028 global small batch batch batch furnace industry research and trend analysis report

Hands on deep learning (32) -- fully connected convolutional neural network FCN

Four common methods of copying object attributes (summarize the highest efficiency)
If you can quickly generate a dictionary from two lists

At the age of 30, I changed to Hongmeng with a high salary because I did these three things

2022-2028 global intelligent interactive tablet industry research and trend analysis report

libmysqlclient.so.20: cannot open shared object file: No such file or directory
Write a mobile date selector component by yourself

2022-2028 global strain gauge pressure sensor industry research and trend analysis report
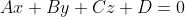
法向量点云旋转
随机推荐
Global and Chinese market of air fryer 2022-2028: Research Report on technology, participants, trends, market size and share
How to batch change file extensions in win10
PHP student achievement management system, the database uses mysql, including source code and database SQL files, with the login management function of students and teachers
直方图均衡化
How do microservices aggregate API documents? This wave of show~
Development trend and market demand analysis report of high purity tin chloride in the world and China Ⓔ 2022 ~ 2027
Reload CUDA and cudnn (for tensorflow and pytorch) [personal sorting summary]
Global and Chinese trisodium bicarbonate operation mode and future development forecast report Ⓢ 2022 ~ 2027
Daughter love: frequency spectrum analysis of a piece of music
Les différents modèles imbriqués de listview et Pageview avec les conseils de flutter
What is permission? What is a role? What are users?
Pueue data migration from '0.4.0' to '0.5.0' versions
【leetcode】29. Divide two numbers
2022-2028 global tensile strain sensor industry research and trend analysis report
PMP registration process and precautions
Some points needing attention in PMP learning
AMLOGIC gsensor debugging
【leetcode】540. A single element in an ordered array
2022-2028 global gasket plate heat exchanger industry research and trend analysis report
Reading notes on how to connect the network - tcp/ip connection (II)