当前位置:网站首页>Trees and graphs (traversal)
Trees and graphs (traversal)
2022-07-04 09:06:00 【Zhuo Mu is not a woodpecker】
Depth-first traversal Example :
Given a tree , The tree contains n Nodes ( Number 1~n) and n-1 Undirected edge .
Please find the center of gravity of the tree , And output after deleting the center of gravity , The maximum number of points in the remaining connected blocks .
Center of gravity definition : The center of gravity is a node in the tree , If you delete this point , The maximum number of points in the remaining connected blocks is the minimum , Then this node is called the center of gravity of the tree .
Input format
The first line contains integers n, Represents the number of nodes in a tree .
Next n-1 That's ok , Each line contains two integers a and b, Indication point a Sum point b There is an edge between .
Output format
Output an integer m, Represents the number of nodes of the largest subtree among all subtrees of the center of gravity .
Data range
1≤n≤105
Input :
9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6
Output :
4
This problem requires depth first traversal , Compare the maximum value in the connected block when each number is taken as the root node , Then compare the minimum value as the result ;
The example of this problem is to 123456789 Delete every number once , The maximum number of points in the connected block after each deletion is 467588888, The minimum value is 4, Output 4;
Code :
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=1e6;
int e[N],n,ne[N],h[N],idx,ans=N,res,s;
bool st[N];
void add(int a,int b) {
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int dfs(int x) {
st[x]=true;
int size=0,sum=1;
for(int i=h[x]; i!=-1; i=ne[i]) {
int j=e[i];
if(st[j]) continue;
int s=dfs(j);
size=max(size,s);
sum+=s;
}
size=max(size,n-sum);
ans=min(size,ans);
return sum;
}
int main() {
cin>>n;
memset(h,-1,sizeof h);
for(int i=0; i<n-1; i++) {
int a,b;
cin>>a>>b;
add(a,b),add(b,a);
}
dfs(1);
cout<<ans;
return 0;
}Breadth first traversal Example :
Given a n A little bit m Directed graph of strip edge , There may be double edges and self rings in the graph .
The length of all edges is 1, The number of the point is 1~n.
Please find out 1 It's on the n The shortest distance of point No , If from 1 Point No. can't go to n Number point , Output -1.
Input format
The first line contains two integers n and m.
Next m That's ok , Each line contains two integers a and b, Indicates that there is a path from a Go to the b The length of is 1 The edge of .
Output format
Output an integer , Express 1 It's on the n The shortest distance of point No .
Data range
1≤n,m≤10^5
Input :
4 5
1 2
2 3
3 4
1 3
1 4
Output :
1
This problem requires depth first traversal , Looking for from 1 To n The smallest path of ;
Use the linked list to store , Look for... In order n, use d Array storage steps , When it finds n when , Output d [ n ];
Code :
#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
const int N=1e6;
int n,m,h[N],e[N],ne[N],idx,d[N];
bool st[N];
queue<int> q;
void add(int a,int b){
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void bfs(int x){
st[x]=true;
d[x]=0;
q.push(x);
while(q.size()){
int v=q.front();
q.pop();
for(int i=h[v];i!=-1;i=ne[i]){
int w=e[i];
if(!st[w]){
st[w]=true;
q.push(w);
d[w]=d[v]+1;
if(w==n) return;
}
}
}
}
int main(){
cin>>n>>m;
d[n]==-1;// Output when not found -1
memset(h,-1,sizeof h);
for(int i=0;i<m;i++){
int a,b;
cin>>a>>b;
add(a,b);
}
bfs(1);
cout<<d[n]<<endl;
return 0;
}边栏推荐
- 20220701 barbarat lemma proof
- awk从入门到入土(6)正则匹配
- Target detection -- intensive reading of yolov3 paper
- After unplugging the network cable, does the original TCP connection still exist?
- Awk from entry to earth (18) GAW K line manual
- Markdown syntax
- Research Report on the development trend and Prospect of global and Chinese zinc antimonide market Ⓚ 2022 ~ 2027
- Mantis creates users without password options
- Turn: excellent managers focus not on mistakes, but on advantages
- The basic syntax of mermaid in typera
猜你喜欢
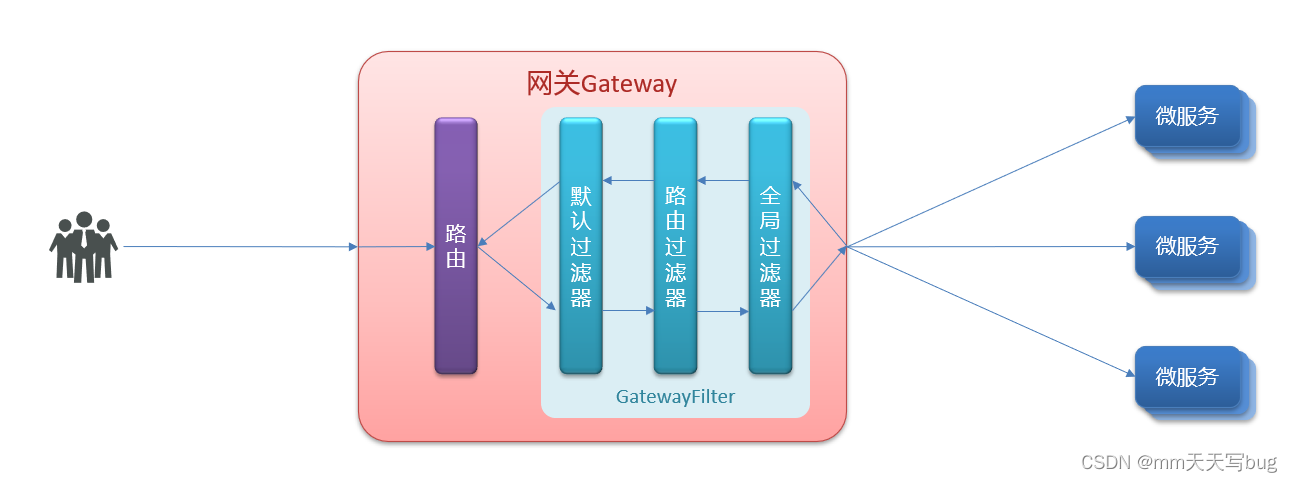
Démarrage des microservices: passerelle
Four essential material websites for we media people to help you easily create popular models

Relationship and operation of random events
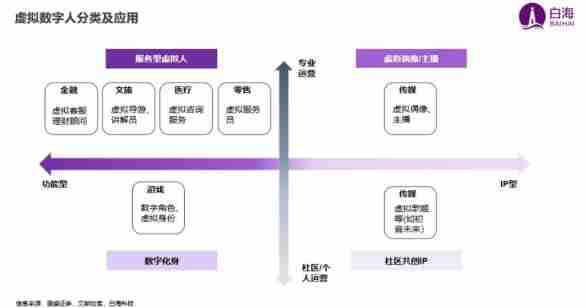
AI Winter Olympics | is the future coming? Enter the entrance of the meta universe - virtual digital human

Codeforces Round #793 (Div. 2)(A-D)
![[C Advanced] file operation (2)](/img/50/e3f09d7025c14ee6c633732aa73cbf.jpg)
[C Advanced] file operation (2)
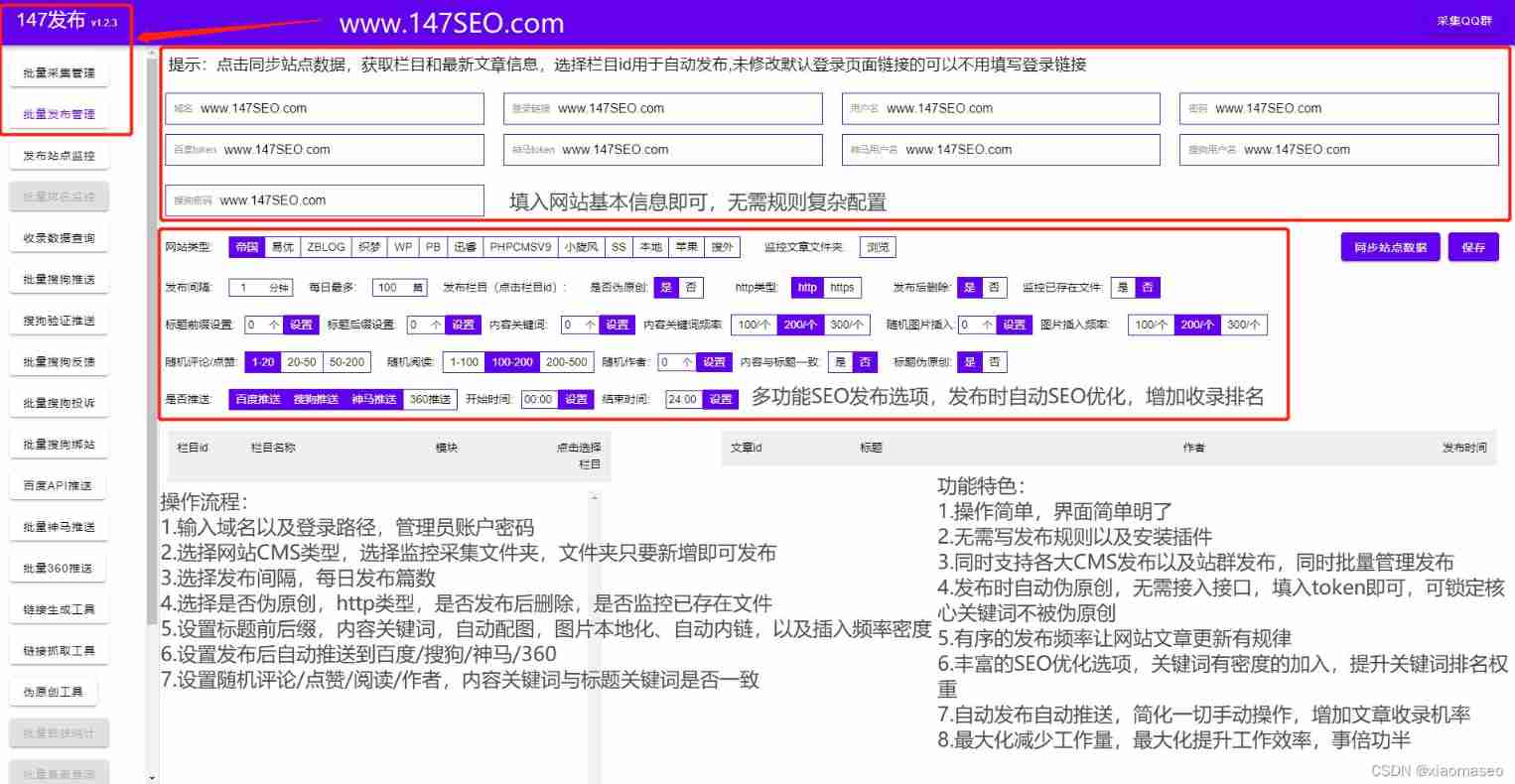
Dede plug-in (multi-function integration)

awk从入门到入土(12)awk也可以写脚本,替代shell
![[error record] no matching function for call to 'cacheflush' cacheflush();)](/img/79/c00f9c835606b2dce1d342ec368d24.jpg)
[error record] no matching function for call to 'cacheflush' cacheflush();)
AMLOGIC gsensor debugging
随机推荐
Tkinter Huarong Road 4x4 tutorial II
awk从入门到入土(14)awk输出重定向
Service call feign of "micro service"
Research Report on the development trend and Prospect of global and Chinese zinc antimonide market Ⓚ 2022 ~ 2027
swatch
Nurse level JDEC addition, deletion, modification and inspection exercise
"How to connect the Internet" reading notes - FTTH
C language - Introduction - Foundation - syntax - [variable, constant light, scope] (V)
Private collection project practice sharing [Yugong series] February 2022 U3D full stack class 007 - production and setting skybox resources
awk从入门到入土(5)简单条件匹配
Report on research and investment prospect prediction of China's electronic grade sulfuric acid industry (2022 Edition)
awk从入门到入土(12)awk也可以写脚本,替代shell
Codeforces Round #793 (Div. 2)(A-D)
C语言-入门-基础-语法-[主函数,头文件](二)
Research Report on the current market situation and development prospects of calcium sulfate whiskers in China (2022 Edition)
Educational Codeforces Round 115 (Rated for Div. 2)
Explain TCP protocol in detail three handshakes and four waves
Awk from getting started to digging in (4) user defined variables
In depth investigation and Strategic Research Report on China's motion controller Market (2022 Edition)
Dede plug-in (multi-function integration)