当前位置:网站首页>CF960G - Bandit Blues(第一类斯特林数+OGF)
CF960G - Bandit Blues(第一类斯特林数+OGF)
2022-07-06 11:34:00 【吃花椒的妙酱】
题意:求有多少个长度为n的排列,满足从左往右取数,得到a个数,从右往左取数,得到b个,其中取数的定义为:若后来者比现在的数大则换掉替换掉现在的数。对998244353取模。
思路:转化一下题意,就是求满足有a个不同前缀最大值、b个不同后缀最大值的排列数。
\qquad 倒着考虑,最后一步一定是取n,所以n前面有a-1个不同前缀最大值,后面有b-1个后缀最大值。两者本质一样的。
思路1 :设f[i][j]为i个数的排列有j个不同前缀最大值的排列数,有转移方程f[i][j] = f[i-1][j-1] + (i-1)*f[i-1][j],f[0][0]=1发现该递推式子和第一类斯特林数的递推式一样
a n s = ∑ i = 0 n − 1 f [ i ] [ a − 1 ] ∗ f [ n − 1 − i ] [ b − 1 ] ∗ C ( n − 1 , i ) ans = \sum_{i=0}^{n-1} f[i][a-1]*f[n-1-i][b-1] * C(n-1,i) ans=∑i=0n−1f[i][a−1]∗f[n−1−i][b−1]∗C(n−1,i),从第一类斯特林数的意义上看,该式子的意思是,前i个数构成a-1个轮转,后n-1-i个数构成b-1个轮转,的排列方案数。
等价于n-1个数构成a+b-2个轮转的方案数,
即ans = f[n-1][a+b-2]*C(a+b-2,a-1)
组合数都会求,第一类斯特林数需要快速求
由于第一类斯特林数的生成函数 ∑ i = 0 n [ n i ] x i = ∏ i = 0 n − 1 ( x + i ) \sum_{i=0}^n{\left[\begin{matrix}n\\i\end{matrix}\right]}x^i=\prod_{i=0}^{n-1}(x+i) ∑i=0n[ni]xi=∏i=0n−1(x+i),可以用分治NTT,O(nlog^n2)求得斯特林数,注意这里求的是 [ n − 1 a + b − 2 ] \left[\begin{matrix}n-1\\a+b-2\end{matrix}\right] [n−1a+b−2](可以用倍增减法卷积nlogn求,本人比较菜不会qaq
思路2: 第一个方程比较难看出来是斯特林数,直接从数学意义上想。
有a-1个不同前缀最大值,b-1个不同后缀最大值,除了a+b-2个位置是固定住的,其他位置的值只要限制在一定范围内,可以任意取,比如说要求4个数提供一个最大值为4的贡献,那么合法的排列是[4,1,2,3],[4,1,3,2],[4,2,1,3],[4,2,3,1],[4,3,1,2],[4,3,2,1],如果要求提供一个2的贡献和4的贡献,则只有一个[2,1,4,3]。就是说,有k个不同的前缀最大值,相当于是k个轮转([4,1,2,3] <=>[1,2,3,4]每个排列经过轮转后一定可以让最大值放第一位置),问题转化成n-1个数构成a+b-2个轮转的方案数,然后就跟思路一一样做了。(比较抽象)
注意特判掉一定不存在的情况。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define IOS ios::sync_with_stdio(false),cin.tie(0)
#define _for(i,a,b) for(int i=(a) ;i<=(b) ;i++)
#define _rep(i,a,b) for(int i=(a) ;i>=(b) ;i--)
#define mst(v,s) memset(v,s,sizeof(v))
#define pii pair<int ,int >
#define pb(v) push_back(v)
#define all(v) v.begin(),v.end()
#define int long long
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
#define endl "\n"
#define fi first
#define se second
#define ls p<<1
#define rs p<<1|1
#define lson p<<1,l,mid
#define rson p<<1|1,mid+1,r
#define AC return 0
#define ldb long double
const int maxn = 6e6+10;
const int p = 998244353;
int Pow(int x,int d){
int tans = 1;
if(d == 0)return 1%p;
int a = Pow(x,d/2);
tans = 1ll*a*a%p;
if(d%2)tans = 1ll*tans*x%p;
return tans%p;
}
typedef vector<int> Poly;//多项式定义
int F1[maxn],F2[maxn];
int rev[maxn];
void NTT(int * A,int lim,int opt) {
int i, j, k, m, gn, g, tmp;
for(int i = 0; i < lim; ++i)rev[i] = (i & 1)*(lim >> 1) + (rev[i >> 1] >> 1);
for(i = 0; i < lim; ++i)if (rev[i] < i) swap(A[i], A[rev[i]]);
for(m = 2; m <= lim; m <<= 1) {
k = m >> 1;
gn = Pow(3,(p - 1) / m);
for(i = 0; i < lim; i += m) {
g = 1;
for (j = 0; j < k; ++j, g = 1ll * g * gn % p) {
tmp = 1ll * A[i + j + k] * g % p;
A[i + j + k] = (A[i + j] - tmp + p) % p;
A[i + j] = (A[i + j] + tmp) % p;
}
}
}
if(opt == -1){
reverse(A+1,A+lim);
int inv = Pow(lim,p-2);
for(i = 0; i < lim; ++i) A[i] = 1ll * A[i] * inv % p;
}
}
Poly mul(const Poly & A,const Poly & B){
int n = A.size(),m = B.size();
int siz = n + m - 1;
Poly C(siz);
if(siz < 64){
//小于等于64项直接暴力算
for(int i = 0;i < n;i++){
for(int j = 0;j < m;j++)C[i+j] = (C[i+j] + 1LL*A[i]*B[j]%p)%p;
}
return C;
}
int fsiz = 1;
while(fsiz <= siz)fsiz *= 2;
for(int i = 0;i < fsiz;i++)F1[i] = F2[i] = 0;
for(int i = 0;i < n;i++)F1[i] = A[i];
for(int i = 0;i < m;i++)F2[i] = B[i];
NTT(F1,fsiz,1);
NTT(F2,fsiz,1);
for(int i = 0;i < fsiz;i++)F1[i] = 1ll*F1[i]*F2[i]%p;
NTT(F1,fsiz,-1);
for(int i = 0;i < siz;i++){
C[i] = F1[i];
}
return C;
}
int n,A,B;
int fac[100005],ni_f[100005];
Poly cal(int l ,int r){
if( l==r ){
Poly ans(2,0);
ans[0] = l;
ans[1] = 1;
return ans;
}
int mid = (l+r)>>1;
return mul(cal(l,mid),cal(mid+1,r));
}
ll qsm(int a,int b,int mod){
a %= mod;
int ans = 1,temp = a;
while(b){
if( b&1 ) ans = (ans * temp)%mod;
temp = (temp * temp)%mod;
b>>=1;
}
return ans;
}
ll C(int n,int m){
return fac[n]*ni_f[n-m]%p*ni_f[m]%p;
}
signed main(){
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
#endif
IOS;
cin>>n>>A>>B;
if( A==0 || B==0 || A+B-2>n-1){
return cout<<0<<endl,0;
}
if( n==1 ){
return cout<<1<<endl,0;
}
Poly f(n+1,0);
f = cal(0,n-2);
fac[0]=1;
_for(i,1,100000) fac[i] = fac[i-1]*i%p;
ni_f[100000] = qsm(fac[100000],p-2,p);
_rep(i,100000-1,0) ni_f[i] = ni_f[i+1] * (i+1)%p;
int ans = C(A+B-2,A-1) * f[A+B-2]%p;
cout<<ans<<endl;
AC;
}
边栏推荐
- Carte de réflexion + code source + notes + projet, saut d'octets + jd + 360 + tri des questions d'entrevue Netease
- 保证接口数据安全的10种方案
- Swagger2 reports an error illegal DefaultValue null for parameter type integer
- 黑馬--Redis篇
- ZABBIX proxy server and ZABBIX SNMP monitoring
- 终于可以一行代码也不用改了!ShardingSphere 原生驱动问世
- 助力安全人才专业素养提升 | 个人能力认证考核第一阶段圆满结束!
- zabbix 代理服务器 与 zabbix-snmp 监控
- Actf 2022 came to a successful conclusion, and 0ops team won the second consecutive championship!!
- AutoCAD - what is the default lineweight for centerline drawing and CAD? Can I modify it?
猜你喜欢
AutoCAD - what is the default lineweight for centerline drawing and CAD? Can I modify it?
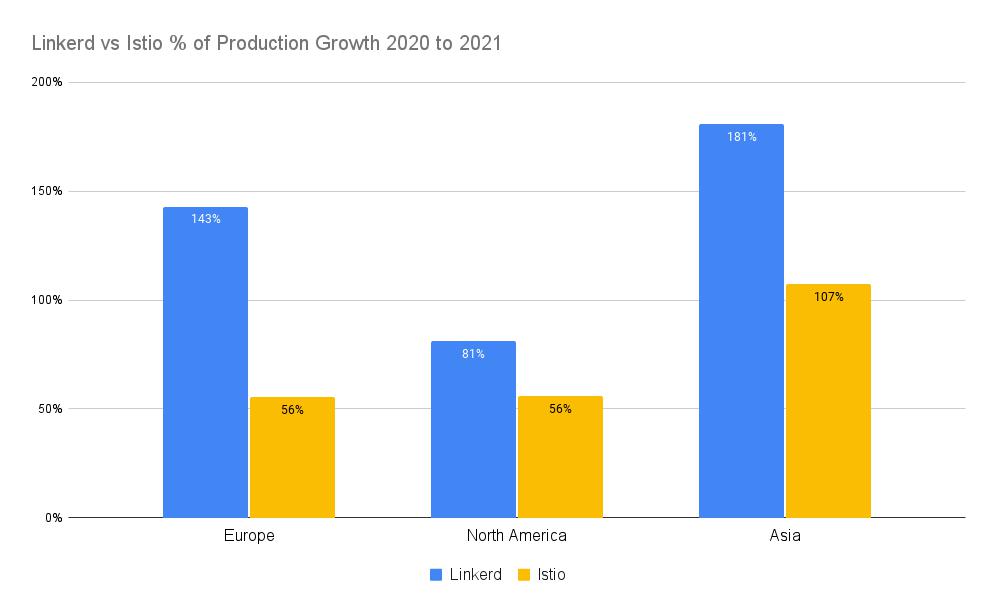
【翻译】Linkerd在欧洲和北美的采用率超过了Istio,2021年增长118%。

ROS自定义消息发布订阅示例
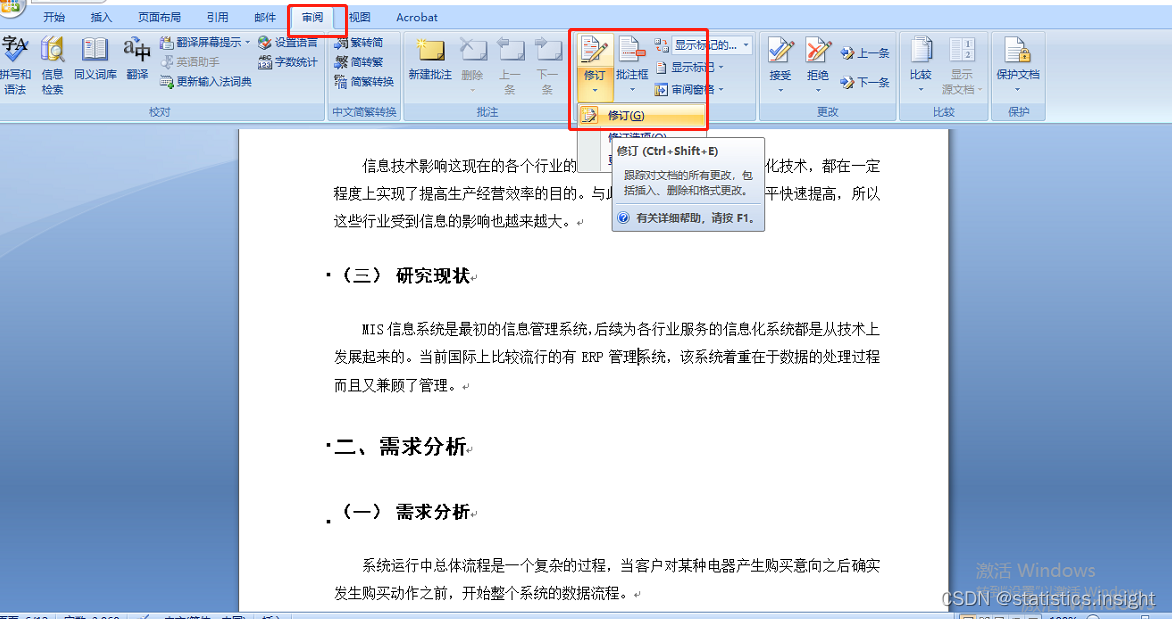
How word displays modification traces
![[paper notes] transunet: transformers make strongencoders for medical image segmentation](/img/21/3d4710024248b62495e2681ebd1bc4.png)
[paper notes] transunet: transformers make strongencoders for medical image segmentation
Abstract classes and abstract methods

【计算情与思】扫地僧、打字员、信息恐慌与奥本海默

Black Horse - - Redis Chapter
zabbix 代理服务器 与 zabbix-snmp 监控

思維導圖+源代碼+筆記+項目,字節跳動+京東+360+網易面試題整理
随机推荐
Sanmian ant financial successfully got the offer, and has experience in Android development agency recruitment and interview
Fast power template for inverse element, the role of inverse element and example [the 20th summer competition of Shanghai University Programming League] permutation counting
黑馬--Redis篇
Help improve the professional quality of safety talents | the first stage of personal ability certification and assessment has been successfully completed!
Druid database connection pool details
Simple understanding of MySQL database
How word displays modification traces
Detailed idea and code implementation of infix expression to suffix expression
学习探索-使用伪元素清除浮动元素造成的高度坍塌
五金机电行业智能供应链管理系统解决方案:数智化供应链为传统产业“造新血”
Solution of commercial supply chain management platform for packaging industry: layout smart supply system and digitally integrate the supply chain of packaging industry
Live broadcast today | the 2022 Hongji ecological partnership conference of "Renji collaboration has come" is ready to go
深入分析,Android面试真题解析火爆全网
面试突击63:MySQL 中如何去重?
Reflection and illegalaccessexception exception during application
R语言ggplot2可视化:使用ggpubr包的ggstripchart函数可视化分组点状条带图(dot strip plot)、设置add参数为不同水平点状条带图添加箱图
How can my Haskell program or library find its version number- How can my Haskell program or library find its version number?
Looting iii[post sequence traversal and backtracking + dynamic planning]
终于可以一行代码也不用改了!ShardingSphere 原生驱动问世
[paper notes] transunet: transformers make strongencoders for medical image segmentation