当前位置:网站首页>Detailed idea and code implementation of infix expression to suffix expression
Detailed idea and code implementation of infix expression to suffix expression
2022-07-06 19:09:00 【Wu Yu 4】
What is infix expression ?
Infix expression is a general expression of arithmetic or logic formula , Operators are in the middle of operands in the form of infixes (eg:3+4、3+4*2、8+(17-6*2)….).
Why do you want infix expression to suffix expression ?
But infix expressions are not easy to be processed by computers . We are calculating an equation ( Usually infix expression ) when , You need to convert infix expression into suffix expression .
What is a suffix expression ?
Then the suffix expression , Also known as reverse Polish , Does not contain brackets , The operator is placed after two operands , All calculations are in the order in which the operators appear , Strictly from left to right ( The precedence rules for operators are no longer considered ). Generally, stack is used to simulate .
How to convert infix expression into suffix expression ?
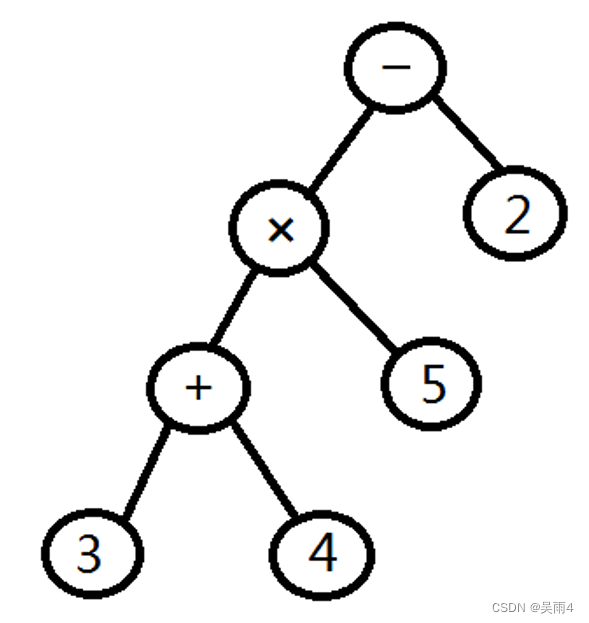
Take a simple chestnut :
(3+4)×5-2
Draw a tree like this :
So the suffix expression is :
3 4 + 5 × 2 -
The following is the idea of transformation :
1. Initialize two character array simulation stacks : Character storage stack s1 And a stack for storing intermediate results s2;
2. Scan infix expressions from left to right ;
3. When it comes to operands , Press it down s2;
4. When an operator is encountered , Compare it with s1 The priority of the top of stack operator :
If s1 It's empty , Or stack top operator is left bracket “(”, This operator will be put on the stack directly ;
otherwise , If the priority is higher than the top of the stack operator , Also push operators into s1;
otherwise , take s1 The operator at the top of the stack pops up and pushes into s2 in , Turn again ① And s1 Compared with the new stack top operators in ;
5. When brackets are encountered :
If it's left parenthesis “(”, Press in directly s1;
If it's right bracket “)”, Then it pops up in turn s1 The operator at the top of the stack , And press in s2, Until we meet the left bracket , This pair of parentheses is discarded ;
6. Repeat step 2 to 5, Up to the far right of the expression ;
7. take s1 The rest of the operators in the pop-up and press in s2;
8. Pop up one by one s2 And output , The reverse order of the result is the suffix expression corresponding to the infix expression
Then it can be calculated according to the suffix expression .
Be sure to pay attention to the calculation order of taking out elements ! The number taken out first is
XCount(X To reduce / except / Add / ride ), The number taken out after isByXCount!
Code ( There are detailed notes ):
#include<bits/stdc++.h>// Universal header file
using namespace std;
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);// Accelerated statement
typedef long long ll;
const int N=1e5+10;
char s1[N],s2[N],s[N];
ll top1,top2,p,js[N],topis;
int lev(char n)
{
if(n=='+'||n=='-') return 1;
if(n=='*'||n=='/') return 2;
if(n=='^') return 3;
return 0;
}
void print()
{
for(int i=1;i<=topis;i++)// Currently being calculated
{
cout<<js[i]<<' ';
}
for(int i=p+1;i<=top2;i++)// Not traversed later
{
cout<<s2[i];
if(i!=top2)
cout<<" ";
}
if(p!=top2)
cout<<endl;
}
int main()
{
cin>>s;
for(int i=0;i<strlen(s);i++)
{
if(s[i]<='9'&&s[i]>='0')
{
s2[++top2]=s[i];
}
else
{
if(s[i]=='(')
{
s1[++top1]=s[i];
continue;
}
if(s1[top1]=='('||top1==0)
{
s1[++top1]=s[i];
continue;
}
if(lev(s1[top1])>=lev(s[i])&&s[i]!=')')// When it comes in, it's not the right bracket , And the incoming symbol priority has no s1 The stack top symbol of has high priority
// At this time, we need to s1 The top element of the stack is given to s2 in
{
s2[++top2]=s1[top1--];
while(lev(s1[top1])>=lev(s[i]))// If the priority level is still not as high as the symbol to enter , Continue to give s2 in
{
s2[++top2]=s1[top1--];
}
// At the end of the cycle , There is no symbol priority to enter s1 The stack top symbol of has high priority , You can deposit s1 in
s1[++top1]=s[i];
continue;
}
if(lev(s1[top1])<lev(s[i])&&s[i]!=')')
{
s1[++top1]=s[i];
}
if(s[i]==')')// Yes ' ) '
{
while(s1[top1]!='(')// take s1 The symbols in are given to s2 in , Until I met ' ) '
{
s2[++top2]=s1[top1--];
}
top1--;
continue;
}
}
}
while(top1>0)// if s1 And symbols , Need to give s2 in
{
s2[++top2]=s1[top1--];
}
for(int i=1;i<=top2;i++)
{
cout<<s2[i]<<" ";
}
cout<<endl;
// Perfect infix to suffix
// Next, calculate
for(int i=1;i<=top2;i++)
{
p=i;
if(s2[i]>='0'&&s2[i]<='9')
{
js[++topis]=s2[i]-'0';
}
else // For the sign , Operate on the two elements at the top of the stack , And store the results on the top of the stack
{
// Pay attention to the first digit of the advanced stack
if(s2[i]=='+')
{
ll x=js[topis];
ll y=js[--topis];
ll ans=y+x;
js[topis]=ans;
}
if(s2[i]=='-')
{
ll x=js[topis];
ll y=js[--topis];
ll ans=y-x;
js[topis]=ans;
}
if(s2[i]=='*')
{
ll x=js[topis];
ll y=js[--topis];
ll ans=y*x;
js[topis]=ans;
}
if(s2[i]=='/')
{
ll x=js[topis];
ll y=js[--topis];
ll ans=y/x;
js[topis]=ans;
}
if(s2[i]=='^')
{
ll x=js[topis];
ll y=js[--topis];
ll ans=pow(y,x);
js[topis]=ans;
}
print();// Print every step
}
}
return 0;
}
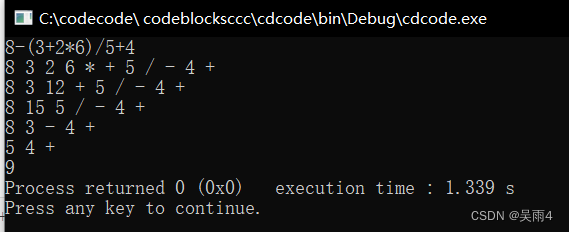
The operation results are as follows :
边栏推荐
- 中缀表达式转后缀表达式详细思路及代码实现
- R语言使用rchisq函数生成符合卡方分布的随机数、使用plot函数可视化符合卡方分布的随机数(Chi Square Distribution)
- Help improve the professional quality of safety talents | the first stage of personal ability certification and assessment has been successfully completed!
- Xingnuochi technology's IPO was terminated: it was planned to raise 350million yuan, with an annual revenue of 367million yuan
- Method of accessing mobile phone storage location permission under non root condition
- 星诺奇科技IPO被终止:曾拟募资3.5亿元 年营收3.67亿
- 助力安全人才专业素养提升 | 个人能力认证考核第一阶段圆满结束!
- AvL树的实现
- 使用map函数、split函数一行键入多个元素
- R language uses rchisq function to generate random numbers that conform to Chi square distribution, and uses plot function to visualize random numbers that conform to Chi square distribution
猜你喜欢
Interview assault 63: how to remove duplication in MySQL?

被疫情占据的上半年,你还好么?| 2022年中总结
Method of accessing mobile phone storage location permission under non root condition
Binary search tree
![[depth first search] Ji suanke: find numbers](/img/e4/708a1e8252bcd2d0d621c66bf6bfed.jpg)
[depth first search] Ji suanke: find numbers
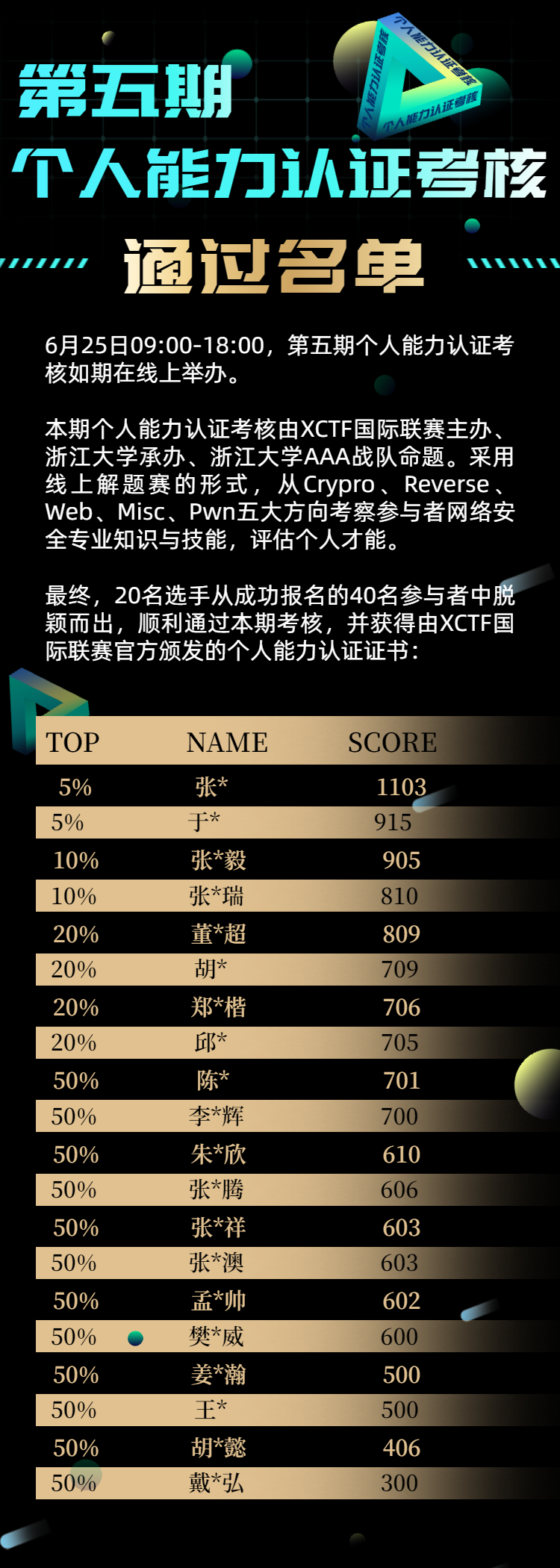
The list of people who passed the fifth phase of personal ability certification assessment was published
三面蚂蚁金服成功拿到offer,Android开发社招面试经验
Simple understanding of MySQL database
多线程基础:线程基本概念与线程的创建
About NPM install error 1
随机推荐
Unlock 2 live broadcast themes in advance! Today, I will teach you how to complete software package integration Issues 29-30
三年Android开发,2022疫情期间八家大厂的Android面试经历和真题整理
Binary search tree
Tensorflow and torch code verify whether CUDA is successfully installed
QPushButton绑定快捷键的注意事项
Jushan database was among the first batch of financial information innovation solutions!
[paper notes] transunet: transformers make strongencoders for medical image segmentation
Precautions for binding shortcut keys of QPushButton
First day of rhcsa study
When visual studio code starts, it prompts "the code installation seems to be corrupt. Please reinstall." Solution to displaying "unsupported" information in the title bar
Modulenotfounderror: no module named 'PIL' solution
Take a look at how cabloyjs workflow engine implements activiti boundary events
Graffiti intelligence is listed on the dual main board in Hong Kong: market value of 11.2 billion Hong Kong, with an annual revenue of 300 million US dollars
Human bone point detection: top-down (part of the theory)
中缀表达式转后缀表达式详细思路及代码实现
根据PPG估算血压利用频谱谱-时间深度神经网络【翻】
Reptiles have a good time. Are you full? These three bottom lines must not be touched!
朗坤智慧冲刺科创板:年营收4亿 拟募资7亿
一种用于夜间和无袖测量血压手臂可穿戴设备【翻译】
用于远程医疗的无创、无袖带血压测量【翻译】