当前位置:网站首页>LeetCode 1175. Prime number arrangement (prime number judgment + Combinatorial Mathematics)
LeetCode 1175. Prime number arrangement (prime number judgment + Combinatorial Mathematics)
2022-07-02 05:04:00 【xylitolz】
List of articles
0 subject

1 Their thinking
1.1 Prime number judgment + Combinatorial mathematics
Ben topic total Of Fang case Count = 「 the Yes quality Count all discharge stay quality Count Cable lead On Of Fang case Count 」 × 「 the Yes close Count all discharge stay close Count Cable lead On Of Fang case Count 」 Total number of schemes in this question =「 The number of schemes in which all prime numbers are placed on the prime index 」\times \\ 「 The number of schemes in which all composite numbers are placed on the composite index 」 Ben topic total Of Fang case Count =「 the Yes quality Count all discharge stay quality Count Cable lead On Of Fang case Count 」×「 the Yes close Count all discharge stay close Count Cable lead On Of Fang case Count 」
「 The number of schemes in which all prime numbers are placed on the prime index 」:
- First of all find out [ 1 , n ] [1,n] [1,n] The number of all prime numbers in the range p r i m e N u m primeNum primeNum
- enumeration 100 All prime numbers within + Two points
- Trial division
- Then find the number of prime numbers primeNum \textit{primeNum} primeNum Of Factorial is the number of schemes
「 The number of schemes in which all composite numbers are placed on the composite index 」:
- n − p r i m e N u m n - primeNum n−primeNum That is, the number of all composite numbers , Then the factorial is the number of schemes
array :
A ( m , n ) = n ! ( n − m ) ! A(m, n) = \frac{n!}{(n - m)!} A(m,n)=(n−m)!n!Combine :
C ( m , n ) = n ! m ! × ( n − m ) ! C(m, n) = \frac{n!}{m! \times (n - m)!} C(m,n)=m!×(n−m)!n!
1.1.1 Code implementation
1.1.1.1 enumeration 100 All prime numbers within + Two points
class Solution {
// enumeration 100 All prime numbers within
private static int[] PRIME = {
2, 3, 5, 7,
11, 13, 17, 19,
23, 29,
31, 37,
41, 43, 47,
53, 59,
61, 67,
71, 73, 79,
83, 89,
97};
private static final int MOD = 1000000007;
public int numPrimeArrangements(int n) {
// Use bisection to find the number of prime numbers
int primeNum = binarySearch(n) + 1;
// Use factorial to find the number of schemes
return (int) (calcFactorial(primeNum) * calcFactorial(n - primeNum) % MOD) ;
}
private long calcFactorial(int m) {
long res = 1;
while (m != 0) {
res *= m;
res %= MOD;
m--;
}
return res;
}
private int binarySearch(int n) {
int left = 0, right = PRIME.length - 1;
while (left < right) {
int mid = left + (right - left + 1) / 2;
if (PRIME[mid] > n) {
right = mid - 1;
} else {
left = mid;
}
}
return left;
}
}
1.1.1.2 Trial division
class Solution {
private static final int MOD = 1000000007;
public int numPrimeArrangements(int n) {
// Try division to get the number of prime numbers
int primeNum = 0;
for (int i = 1; i <= n; i++) {
if (isPrime(i)) {
primeNum++;
}
}
// Use factorial to find the number of schemes
return (int) (calcFactorial(primeNum) * calcFactorial(n - primeNum) % MOD);
}
public boolean isPrime(int n) {
if (n == 1) {
return false;
}
for (int i = 2; i * i <= n; i++) {
if (n % i == 0) {
return false;
}
}
return true;
}
public long calcFactorial(int n) {
long res = 1;
for (int i = 1; i <= n; i++) {
res *= i;
res %= MOD;
}
return res;
}
}
2 Reference
边栏推荐
猜你喜欢

Idea autoguide package and autodelete package Settings

解析少儿编程中的动手搭建教程

Practical problem solving ability of steam Education

Orthogonal test method and function diagram method for test case design
![[understand one article] FD_ Use of set](/img/57/276f5ef438adee2cba31dceeabb95c.jpg)
[understand one article] FD_ Use of set
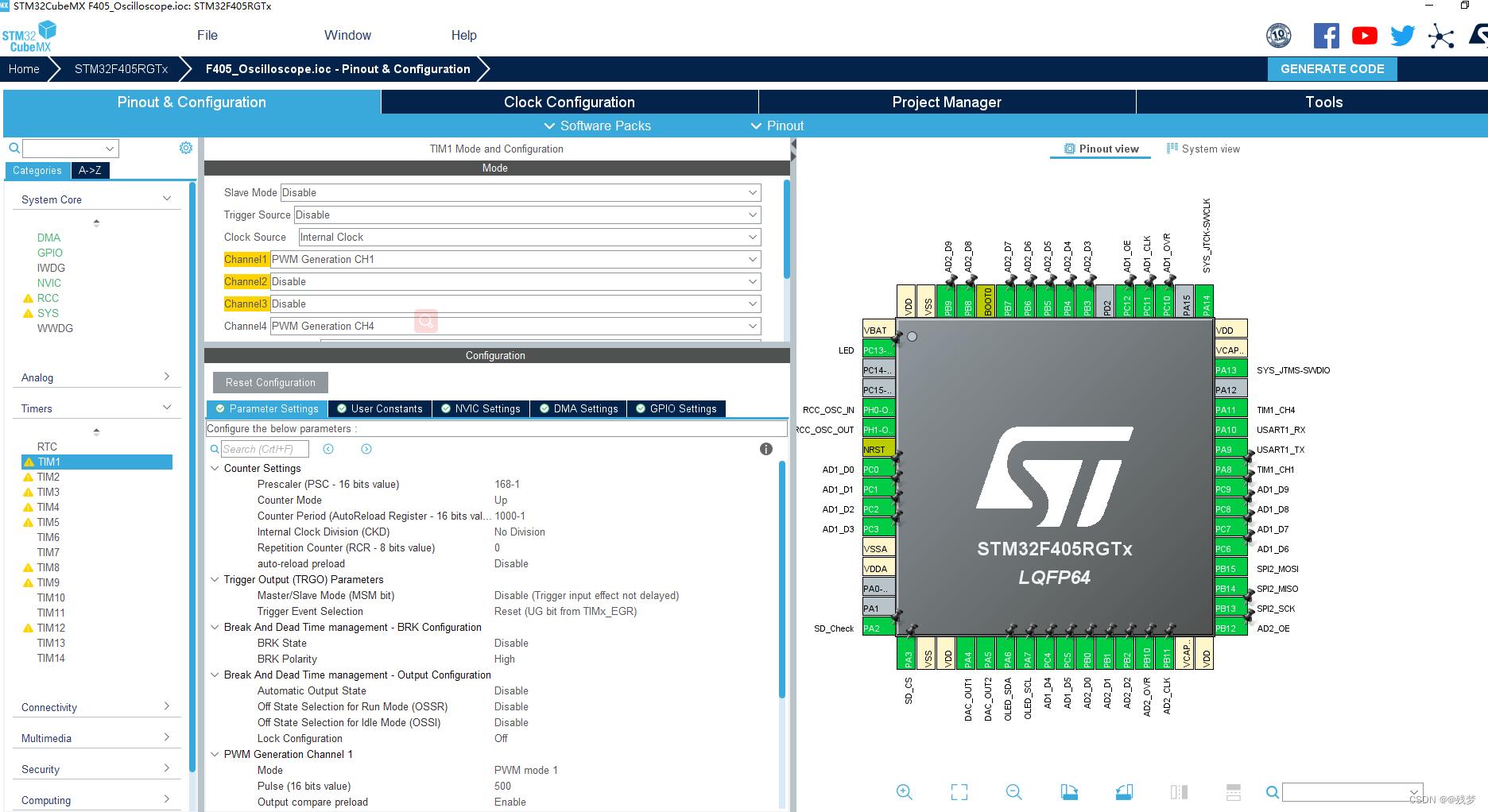
CubeMx DMA笔记
数据库问题汇总

paddle: ValueError:quality setting only supported for ‘jpeg‘ compression

Common errors of dmrman offline backup

Typescript function details
随机推荐
Rhcsa --- work on the third day
Precipitate yourself and stay up late to sort out 100 knowledge points of interface testing professional literacy
Realize the function of data uploading
6.30年终小结,学生时代结束
Ansible installation and use
Rhcsa --- work on the fourth day
Pytest learning ----- pytest assertion of interface automation testing
Record my pytorch installation process and errors
[common error] the DDR type of FPGA device is selected incorrectly
el-cascader回显只选中不显示的问题
Getting started with pytest -- description of fixture parameters
TypeScript类的使用
Line by line explanation of yolox source code of anchor free series network (7) -- obj in head_ loss、Cls_ Loss and reg_ Calculation and reverse transmission of loss I
函数中使用sizeof(arr) / sizeof(arr[0])求数组长度不正确的原因
The underlying principle of go map (storage and capacity expansion)
数学知识——快速幂的理解及例题
TypeScript函数详解
2022-003arts: recursive routine of binary tree
LeetCode 241. 为运算表达式设计优先级(分治/记忆化递归/动态规划)
Here comes the chicken soup! Keep this quick guide for data analysts