Summary
Linear regression is the basis of logical regression , Logistic regression is also a part of neural network , For resolution 2 Classification problem
Linear regression is the basis of all algorithms
linear relationship And Nonlinear relation
Concept :
- Linear relationship means that the relationship between variables is Once function , An argument x And dependent variables y The relationship between is expressed as A straight line , Two independent variables and dependent variables y The relationship between is expressed as A plane
- Nonlinear relation refers to an independent variable x And dependent variables y The relationship between is expressed as A curve , Two independent variables and dependent variables y The relationship between is expressed as A surface
An argument x It is equivalent to a feature , When fitting, it is a line , And if there are multiple features , Is the fitting surface
The linear relation can be understood as a function of degree , No matter how many arguments there are
Example :
- linear relationship :$$y = a\times x + b$$
- Nonlinear relation :$$y = x^2$$
The return question
Concept : Predict a Continuous problem The numerical ,
Linear regression is mainly used to deal with regression problems , A few cases are used to deal with classification problems
Univariate linear regression
Concept : There is only one independent variable and dependent variable ( An independent variable is called a unary ) The situation of , And there is a linear relationship between the independent variable and the dependent variable ( Once function ) The regression model of
Representation form :$$y = a \times x + b$$
Only x One The independent variables ,y by The dependent variable ,a by Slope , Also known as x The weight of ,b by intercept
effect : Find a suitable straight line through the univariate linear regression model , Best fit the independent variables x And dependent variables y The relationship between , So we know one x Value , You can find the most possible through this fitting line y
The process of learning univariate linear model is to get the appropriate through training data a and b The process of , That is, the parameters of the univariate linear model are a and b, When entering a new test data point , We can predict through the trained model .
How to evaluate the quality of the model
The goal is : The smaller the difference between the predicted value and the real value, the better , The smaller the distance , The better the effect of our model
A natural idea is : For each of these points (x) All are calculated
Then add up all the values and divide by the number of samples , This is to reduce the impact of samples on the results .
The formula :
The problem with this formula : The predicted value may be greater than the real value or less than the real value , This will cause errors to be weakened , Positive and negative neutralization leads to the final cumulative error close to 0
improvement : Calculate the absolute value of the error of each point , That is to say \(|y^i-y\_predict^i|\), Then we add up
problem : Subsequent error calculation and derivation problems
Absolute value function , such as $$y = |x|$$ stay x=0 Continuous , But in x The left derivative at is -1, The right derivative is 1, It's not equal , Derivable functions must be smooth , So the function is x=0 Do not guide
Further optimization : For each point, the calculated error , Square the result once , And in order to ignore the influence of the number of samples , Average.
The formula :
Least square method
because
Substitute into the formula in the previous section
Find the optimal parameters by the least square method a and b, So that the expression is as small as possible
Concept : A mathematical optimization technique , Find the optimal parameters by minimizing the sum of squares of errors
The formula :
Code implementation
import numpy as np
from matplotlib import pyplot as plt
if __name__ == '__main__':
# Prepare the data
x = np.array([1, 2, 4, 6, 8]) # Univariate linear regression model only deals with vectors , Instead of dealing with matrices
y = np.array([2, 5, 7, 8, 9])
x_mean = np.mean(x)
y_mean = np.mean(y)
# seek a and b
denominator = 0.0 # The denominator
numerator = 0.0 # molecular
for x_i, y_i in zip(x, y): # take x, y Vectors are combined to form tuples (1, 2)、(2, 5)
numerator += (x_i - x_mean) * (y_i - y_mean)
denominator += (x_i - x_mean) ** 2
a = numerator / denominator
b = y_mean - a * x_mean
# use a and b Construct a linear function , The output prediction value is stored in y_predict
y_predict = a * x + b # This function is a good fit to the training set x Of
# Draw this straight line , And the data of the training set
plt.scatter(x, y, color='b')
plt.plot(x, y_predict, color='r')
plt.xlabel('x', fontsize=15)
plt.ylabel('y', fontsize=15)
plt.show()
# Input test data , Return to a value
x_test = 7
y_predict_test = a * x_test + b
print(y_predict_test)
Univariate linear regression model only deals with vectors , Instead of dealing with matrices
After some encapsulation :
import numpy as np
import matplotlib.pyplot as plt
class SimpleLinearRegressionSelf:
# Initialize variable
def __init__(self):
""" initialization simple linear regression Model """
self.a_ = None # Use in class , Non user external input variables
self.b_ = None # Use in class , Non user external input variables
# Training models
def fit(self, x_train, y_train):
assert x_train.ndim == 1
x_mean = np.mean(x_train)
y_mean = np.mean(y_train)
denominator = 0.0
numerator = 0.0
for x_i, y_i in zip(x_train, y_train):
numerator += (x_i - x_mean) * (y_i - y_mean)
denominator += (x_i - x_mean) ** 2
self.a_ = numerator / denominator
self.b_ = y_mean - self.a_ * x_mean
return self
# forecast
def predict(self, x_test_group): # The input is a set of vectors
# Make a prediction for each vector in the input vector set , The specific implementation of prediction is encapsulated in _predict Function
return np.array([self._predict(x_test) for x_test in x_test_group])
def _predict(self, x_test):
# Find each input x_test To get the predicted value
return self.a_ * x_test + self.b_
# Measure model scores
def mean_squared_error(self, y_true, y_predict):
return np.sum((y_true - y_predict) ** 2) / len(y_true)
def r_square(self, y_true, y_predict):
# Calculate the specified data ( Array elements ) Variance along the specified axis
return 1 - (self.mean_squared_error(y_true, y_predict) / np.var(y_true))
if __name__ == '__main__':
x = np.array([1, 2, 4, 6, 8])
y = np.array([2, 5, 7, 8, 9])
lr = SimpleLinearRegressionSelf()
lr.fit(x, y)
print(lr.predict([7]))
print(lr.r_square([8, 9], lr.predict([6, 8])))
Here, the formula to measure the model score is :
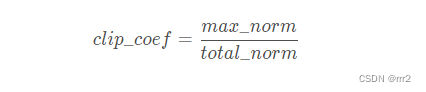

![[mask requirements of OSPF and Isis in multi access network]](/img/7d/1ba80bb906caa9be4bef165ac26d2c.png)

![[effective Objective-C] - memory management](/img/1e/611aa998486bbac76ac103c3091794.jpg)