当前位置:网站首页>求各种极限的方法
求各种极限的方法
2022-07-01 18:44:00 【Debroon】
直接代入型
- lim x − > 3 ( x + 1 ) \lim\limits_{x->3}(x+1) x−>3lim(x+1)
x 的极限接近3,就是在 3 附近,我们直接把 x=3 代入 x+1 中计算,得 4.
有一些特例:
- 常 数 ∞ = 0 \frac{常数}{∞}=0 ∞常数=0
- ∞ 常 数 = ∞ \frac{∞}{常数}=∞ 常数∞=∞
- 非 零 常 数 0 = ∞ \frac{非零常数}{0}=∞ 0非零常数=∞
- ∞ > 0 = ∞ ∞^{>0}=∞ ∞>0=∞
- ∞ < 0 = 1 ∞ > 0 = 0 ∞^{<0}=\frac{1}{∞^{>0}}=0 ∞<0=∞>01=0
- n ∞ = 0 , 0 > n > 1 n^{∞}=0,0>n>1 n∞=0,0>n>1
- n ∞ = ∞ , n > 1 n^{∞}=∞,n>1 n∞=∞,n>1
∞ ∞ \frac{∞}{∞} ∞∞ 型
一些题目直接代入是无解的,比如 ∞ ∞ \frac{∞}{∞} ∞∞ 型,算出来不是一个具体数字,而是一个趋势。
- lim x − > ∞ x 100 + x − 1001 + x x 1000 + 2 x \lim\limits_{x->∞}\frac{x^{100}+x^{-1001}+x}{x^{1000}+2x} x−>∞limx1000+2xx100+x−1001+x
解法:抓主要趋势
在很多个趋势(∞)里,我们要找到最大的那个趋势,因为那个才是影响最大的项。
∞ ∞ \frac{∞}{∞} ∞∞ 型,求解步骤:
- 找出趋势
- 看指数,分子、分母保留最大的趋势
lim x − > ∞ x 100 + x − 1001 + x x 1000 + 2 x \lim\limits_{x->∞}\frac{x^{100}+x^{-1001}+x}{x^{1000}+2x} x−>∞limx1000+2xx100+x−1001+x
- = lim x − > ∞ ∞ 100 + ∞ − 1001 + ∞ ∞ 1000 + 2 ∞ \lim\limits_{x->∞}\frac{∞^{100}+∞^{-1001}+∞}{∞^{1000}+2∞} x−>∞lim∞1000+2∞∞100+∞−1001+∞
- = lim x − > ∞ ∞ + 0 + ∞ ∞ + ∞ \lim\limits_{x->∞}\frac{∞+0+∞}{∞+∞} x−>∞lim∞+∞∞+0+∞
- = lim x − > ∞ x 100 x 1000 \lim\limits_{x->∞}\frac{x^{100}}{x^{1000}} x−>∞limx1000x100
- = lim x − > ∞ 1 x 900 \lim\limits_{x->∞}\frac{1}{x^{900}} x−>∞limx9001
- = lim x − > ∞ 1 ∞ 900 \lim\limits_{x->∞}\frac{1}{∞^{900}} x−>∞lim∞9001
- = 1 ∞ \frac{1}{∞} ∞1
- = 0 0 0
解法:用洛必达法则
0 0 \frac{0}{0} 00 型
lim x − > 0 x s i n x = 0 0 \lim\limits_{x->0}\frac{x}{sinx}=\frac{0}{0} x−>0limsinxx=00
当把 x − > 0 x->0 x−>0 代入式子后,会变成 0 0 \frac{0}{0} 00,也会出现无解的情况。
解法:用等价无穷小代换
当某部分趋向 0 时,有五种情况:
第一种情况, x − > 0 , s i n x = x x->0,sin x = x x−>0,sinx=x,
- lim x − > 0 x s i n x = x x = 1 \lim\limits_{x->0}\frac{x}{sinx}=\frac{x}{x}=1 x−>0limsinxx=xx=1
第二种情况, 1 − c o s Δ 1-cos\Delta 1−cosΔ 可变为 1 2 Δ 2 \frac{1}{2}\Delta^{2} 21Δ2
- lim x − > 0 1 − c o s x x = lim x − > 0 1 2 x 2 x \lim\limits_{x->0}\frac{1-cosx}{x}=\lim\limits_{x->0}\frac{\frac{1}{2}x^{2}}{x} x−>0limx1−cosx=x−>0limx21x2
后续三种情况性质同上,都是代换形式。
解法:用洛必达法则
若将未知数 x − > 0 、 x − > ∞ x->0、x->∞ x−>0、x−>∞ 代入后,式子是 0 0 \frac{0}{0} 00 or ∞ ∞ \frac{∞}{∞} ∞∞ ,则 lim f ( x ) g ( x ) = lim f ′ ( x ) g ′ ( x ) \lim\limits \frac{f(x)}{g(x)}=\lim\limits \frac{f'(x)}{g'(x)} limg(x)f(x)=limg′(x)f′(x),分子变成分子的导数、分母变成分母的导数。
∞ ⋅ 0 ∞·0 ∞⋅0 型
lim x − > ∞ x ( c o s 1 x − 1 ) \lim\limits_{x->∞}x(cos\frac{1}{x}-1) x−>∞limx(cosx1−1)
- = ∞ · (cos 0 - 1)
- = ∞ · 0
直接代入遇到 ∞ ⋅ 0 ∞·0 ∞⋅0,也算不出结果。
我们有另外的解法:
- 找到最简单的一项 a
- 把此项变成 1 1 a \frac{1}{\frac{1}{a}} a11
lim x − > ∞ x ( c o s 1 x − 1 ) \lim\limits_{x->∞}x(cos\frac{1}{x}-1) x−>∞limx(cosx1−1)
- = lim x − > ∞ 1 1 x ( c o s 1 x − 1 ) \lim\limits_{x->∞}\frac{1}{\frac{1}{x}}(cos\frac{1}{x}-1) x−>∞limx11(cosx1−1)
- = lim x − > ∞ c o s 1 x − 1 1 x \lim\limits_{x->∞}\frac{cos\frac{1}{x}-1}{\frac{1}{x}} x−>∞limx1cosx1−1
- = 0 0 \frac{0}{0} 00
指数、底数都有 x 的极限
形如: lim x − > 0 ( 1 + 3 x ) 2 s i n x \lim\limits_{x->0}(1+3x)^{\frac{2}{sinx}} x−>0lim(1+3x)sinx2
把 底 数 指 数 底数^{指数} 底数指数 变成 e 指 数 ⋅ l n 底 数 e^{指数·ln底数} e指数⋅ln底数
lim x − > 0 ( 1 + 3 x ) 2 s i n x = lim x − > 0 e 2 s i n x l n ( 1 + 3 x ) \lim\limits_{x->0}(1+3x)^{\frac{2}{sinx}}=\lim\limits_{x->0}e^{\frac{2}{sinx}ln(1+3x)} x−>0lim(1+3x)sinx2=x−>0limesinx2ln(1+3x)
= lim x − > 0 e 2 l n ( 1 + 3 x ) s i n x \lim\limits_{x->0}e^{\frac{2ln(1+3x)}{sinx}} x−>0limesinx2ln(1+3x)
lim x − > ? e 指 数 = e lim x − > ? 指 数 \lim\limits_{x->?}e^{指数}=e^{\lim\limits_{x->?}指数} x−>?lime指数=ex−>?lim指数
= e lim x − > 0 2 l n ( 1 + 3 x ) s i n x e^{\lim\limits_{x->0}}{\frac{2ln(1+3x)}{sinx}} ex−>0limsinx2ln(1+3x)
函数的左右极限
需要求左右极限的情形
有三种情况的极限,只能通过最原始的方法 — 左右极限来求。
- 第一类,函数是带大括号的分段函数,要求的极限是在分段点处的极限。
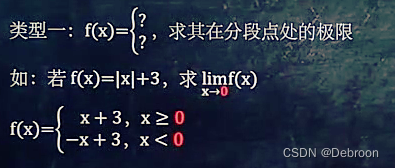
- 第二类,数 g ( x ) g^{(x)} g(x) 在 g ( x ) g(x) g(x) 的分母为 0 处的极限。

- 第三类, a r c t a n g ( x ) arctan ~g(x) arctan g(x) 在 g ( x ) g(x) g(x) 的分母为 0 处的极限

做题方法:
- 先求左极限、右极限
- 当左极限 = 右极限 = 不为 ∞ 的数时,函数极限存在,且极限 = 左极限 = 右极限
- 当左极限 = 右极限 = -∞ 或者 +∞ 时,函数极限为 ∞ / 不存在 / 没有极限
- 当左极限 != 右极限 且 存在不为 ∞ 的值时,函数极限不存在 且 不为 ∞
边栏推荐
- Gameframework eating guide
- Chaos engineering platform chaosblade box new heavy release
- PMP是被取消了吗??
- M91 fast hall measuring instrument - better measurement in a shorter time
- 【6.24-7.1】写作社区精彩技术博文回顾
- Lake Shore 连续流动低温恒温器传输线
- Cdga | if you are engaged in the communication industry, you should get a data management certificate
- M91快速霍尔测量仪—在更短的时间内进行更好的测量
- 【Go ~ 0到1 】 第四天 6月30 defer,结构体,方法
- 物联网平台thingsboard搭建学习记录
猜你喜欢

线程的并行、并发、生命周期

Altair HyperWorks 2022 software installation package and installation tutorial

Lake Shore—OptiMag 超导磁体系统 — OM 系列

C-end dream is difficult to achieve. What does iFLYTEK rely on to support the goal of 1billion users?

Intensive cultivation of channels for joint development Fuxin and Weishi Jiajie held a new product training conference

混沌工程平台 ChaosBlade-Box 新版重磅发布

水产行业智能供应链管理平台解决方案:支撑企业供应链数字化,提升企业管理效益

Getting started with kubernetes command (namespaces, pods)
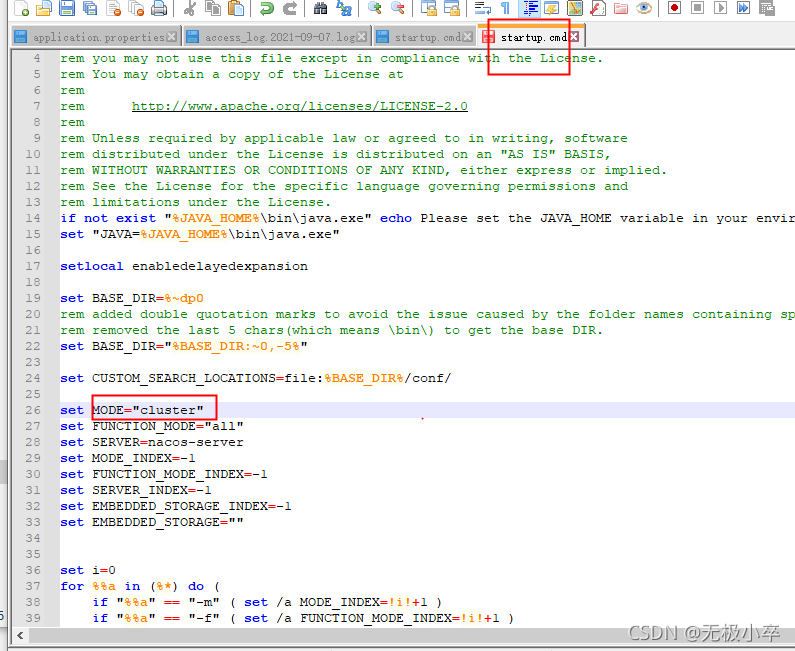
nacos启动失败问题解决与总结

Huawei cloud experts explain the new features of gaussdb (for MySQL)
随机推荐
sql查询去重统计的方法总结
Cache problems after app release
VBA simple macro programming of Excel
华为游戏初始化init失败,返回错误码907135000
制造业SRM管理系统供应商全方位闭环管理,实现采购寻源与流程高效协同
Specification of lumiprobe reactive dye indocyanine green
Cdga | if you are engaged in the communication industry, you should get a data management certificate
Technical secrets of ByteDance data platform: implementation and optimization of complex query based on Clickhouse
Summary of cases of players' disconnection and reconnection in Huawei online battle service
生鲜行业B2B电商平台解决方案,提高企业交易流程标准化和透明度
[6.24-7.1] review of wonderful technical blog posts in the writing community
Chaos engineering platform chaosblade box new heavy release
助力数字经济发展,夯实数字人才底座—数字人才大赛在昆成功举办
How to use the low code platform of the Internet of things for personal settings?
nacos启动失败问题解决与总结
【森城市】GIS数据漫谈(一)
论文阅读【Discriminative Latent Semantic Graph for Video Captioning】
Gameframework eating guide
Nacos configuration file publishing failed, please check whether the parameters are correct solution
Lumiprobe phosphide hexaethylene phosphide specification