[CV] Wu Enda machine learning course notes | Chapter 12

If there is no special explanation in this series of articles , The text explains the picture above the text
machine learning | Coursera
Wu Enda machine learning series _bilibili

12 Support vector machine （SVM）

12-1 Optimization objectives

• The coordinate system on the left of the above figure is $y=1$ Image of time valence function , Support vector machine draws a pink curve , Name it $Cos{t}_1(z)$, Subscript refers to $y$ The value of is $1$
• alike , The right coordinate system is $y=0$ Image of time valence function , Support vector machine draws a pink curve , Name it $Cos{t}_0(z)$, Subscript refers to $y$ The value of is $0$

In logical regression , The cost function is ：
$$J(\theta )=-\frac{1}{m}\left[\sum _{i=1}^m{y}^{(i)}log(h_{\theta }(x^{(i)}))+(1-y^{(i)})log(1-h_{\theta }(x^{(i)}))\right]+\frac{\lambda }{2m}\sum _{j=1}^n{\theta }_j^2$$
Support vector machine , First put the minus sign in the above formula into the sum , And then put $\frac{1}{m}$ Get rid of （$\frac{1}{m}$ It's a constant , Although removing it will change the value of the cost function , But the same minimum value can still be obtained $\theta$）, The resulting cost function is ：
$$J(\theta )=\sum _{i=1}^m\left[y^{(i)}\left(-log(h_{\theta }(x^{(i)}))\right)+(1-y^{(i)})\left(-log(1-h_{\theta }(x^{(i)}))\right)\right]+\frac{\lambda }{2}\sum _{j=1}^n{\theta }_j^2$$
Put... In the above formula $\left(-log(h_{\theta }(x^{(i)}))\right)$ Replace with $Cos{t}_1({\theta }^T{x}^{(i)})$, hold $\left(-log(1-h_{\theta }(x^{(i)}))\right)$ Replace with $Cos{t}_0({\theta }^T{x}^{(i)})$, Get the cost function ：
$$J(\theta )=\sum _{i=1}^m\left[y^{(i)}Cos{t}_1({\theta }^T{x}^{(i)})+(1-y^{(i)})Cos{t}_0({\theta }^T{x}^{(i)})\right]+\frac{\lambda }{2}\sum _{j=1}^n{\theta }_j^2$$
In support vector machines , No longer use regularization parameters $\lambda$, Use parameters instead $C$, The cost function of the changed support vector machine is ：
$$J(\theta )=C\sum _{i=1}^m\left[y^{(i)}Cos{t}_1({\theta }^T{x}^{(i)})+(1-y^{(i)})Cos{t}_0({\theta }^T{x}^{(i)})\right]+\frac{1}{2}\sum _{j=1}^n{\theta }_j^2$$

• Support vector machines do not predict $y=1/0$ Probability , If ${\theta }^T{x}^{(i)}\ge 0$, Suppose the function output 1, On the contrary, output 0

12-2 Understanding of large spacing

Support vector machine is also called large space classifier

Change the judgment boundary in support vector machine , Give Way ${\theta }^T{x}^{(i)}\ge 1$ When the output 1,${\theta }^T{x}^{(i)}\le -1$ When the output 0, In this way, there is a safe gap between the two results

Using a general logistic regression algorithm may generate pink and green lines in the above figure to segment two types of samples , And use support vector chance to generate black lines in the figure , The area between the two blue lines in the figure is called the spacing , Support vector machines try to separate the two samples with the greatest spacing , It can be seen that , Support vector machine can have better robustness

Pictured above , Let's assume that there is no negative sample on the left , Use a big $C$ The black line in the above figure can be generated , But if there is a negative sample on the left , because $C$ It's big , Support vector machine is used to ensure the maximum distance between two kinds of samples , The pink line in the above figure will be generated , But if $C$ It's not that big , Then even if there is a negative sample on the left , Black lines will still be generated

• $C$ It's equivalent to the previous $\frac{1}{\lambda }$, Although the two are really different , But the effect is similar

12-3 Mathematical principle of support vector machine

12-4 Kernel function I

The sample shown in the figure , If we assume that the function $\ge 0$, Just predict $y=1$, Other predictions $y=0$,
In the hypothetical function in the figure above , set up $f_1=x_1,f_2=x_2,f_3=x_1{x}_2,f_4=x_1^2,...$
Suppose the function becomes $h_{\theta }(x)={\theta }_0+{\theta }_1{f}_1+{\theta }_2{f}_2+...$
The above method has nothing to do with the following method , Independent of kernel function
However , In addition to combining the original features , Is there a better way to construct 𝑓1, 𝑓2, 𝑓3？ We can use kernel function to calculate new features .

Take... In the coordinate system 3 Sample marking matrix $l^{(1)}、l^{(2)}、l^{(3)}$
$x$ Is a given training example , Suppose there are two eigenvalues , that $x=[x_1,x_2]$
Make
$$f_1=similarity\left(x,l^{(1)}\right)=exp\left(-\frac{\Vert x-l^{(1)}{\Vert }^2}{2{\sigma }^2}\right)$$
$$f_2=similarity\left(x,l^{(2)}\right)=exp\left(-\frac{\Vert x-l^{(2)}{\Vert }^2}{2{\sigma }^2}\right)$$
$$f_3=......$$
$$......$$

• $similarity\left(x,l^{(i)}\right)$ It is called similarity measure function / Kernel function
• $similarity\left(x,l^{(i)}\right)$ It can also be written as $k\left(x,l^{(i)}\right)$
• $exp(x)$ Express $e^x$, It is called Gaussian kernel function
• ${\sigma }^2$ Is the parameter of Gaussian kernel function

The kernel function can be reduced to ：
$$f_1=similarity\left(x,l^{(1)}\right)=exp\left(-\frac{\Vert x-l^{(1)}{\Vert }^2}{2{\sigma }^2}\right)=exp\left(-\frac{{\sum }_{j=1}^n(x_j-l_j^{(1)}{)}^2}{2{\sigma }^2}\right)$$

If $x$ Very close to the mark $l^{(1)}$, that $f_1\approx exp(-\frac{0^2}{2{\sigma }^2})\approx 1$
If $x$ Stay away from the mark $l^{(1)}$, that $f_1\approx exp(-\frac{(largenumber{)}^2}{2{\sigma }^2})\approx 0$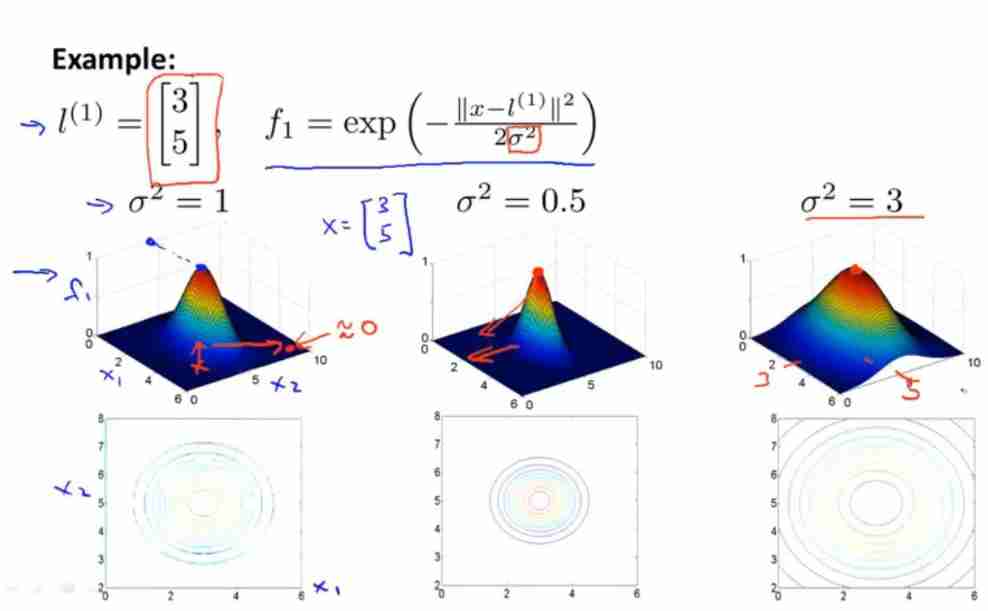

Upper figure , If ${\sigma }^2$ Bigger , that $f_i$ The descent speed of will slow down （ The slope decreases ）

Pictured above , Take a little $x$, It has been calculated by support vector machine ${\theta }_0、{\theta }_1、...$ The value of is shown in the figure above , Then we can calculate according to the kernel function $f_0、f_1、...$ The value of is shown in the figure above , take $\theta$ and $f$ The value of is substituted into the assumed function to get $0.5\ge 0$, So predict $y=1$

Pictured above , Take another point $x$, hypothesis ： Finally get close $l^{(1)}and{l}^{(2)}$ The point of will be predicted as 1, And away $l^{(1)}and{l}^{(2)}$ The point of will be predicted as 0, Finally, you can fit a red curve as shown in the figure , The prediction in the curve is 1, The prediction outside the curve is 0

12-5 Kernel function II

How to choose landmarks ？
　　 We usually choose the number of landmarks according to the number of training sets , That is, if there is 𝑚 An example , Then we choose
take 𝑚 Landmarks , And make :𝑙(1) = 𝑥(1), 𝑙(2) = 𝑥(2), . . . . . , 𝑙(𝑚) = 𝑥(𝑚). The advantage of doing so is ： Now we
The new features are based on the distance between the original features and all other features in the training set , namely ：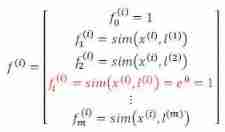


from
$f_1^{(i)}=similarity\left(x^{(i)},l^{(1)}\right)$
$f_2^{(i)}=similarity\left(x^{(i)},l^{(2)}\right)$
$...$
$f_m^{(i)}=similarity\left(x^{(i)},l^{(m)}\right)$
take $f$ Write as eigenvector form to get
$$f^{(i)}=\left[\begin{array}{c}{f}_0^{(i)}=1\\ f_1^{(i)}\\ f_2^{(i)}\\ ...\\ f_m^{(i)}\end{array}\right]$$
$f^{(i)}$ It's a $m+1$ D matrix , Because except for $m$ Out of samples , A bias term is also added $f_0^{(i)}=1$
matrix $f^{(i)}$ The meaning is ( The first $i$ All the features in the samples ) And ( from 1 To m All the features in each sample ) Perform kernel operation , altogether m The operation results are arranged in the matrix , And add the 0 One of the $f_0^{(i)}=1$

use $f^{(i)}$ Replacement tape $x$ term , The cost function obtained is ：
$$C\sum _{i=1}^m\left[y^{(i)}Cos{t}_1({\theta }^T{f}^{(i)})+(1-y^{(i)})Cos{t}_0({\theta }^T{f}^{(i)})\right]+\frac{1}{2}\sum _{j=1}^{n=m}{\theta }_j^2$$

• On the regularization term $n=m$ The explanation of ：${\theta }_{(i)}$ Is corresponding to matrix $f^{(i)}$ The weight of , Because there are $i=1,2,...,m$ common m individual $f^{(i)}$ Corresponding m individual $\theta$, So let's assume that there are m term , That is to say m individual $\theta$, And the weight has been specified before $\theta$ Number of n To express , So there's $n=m$ Note that this has been ignored ${\theta }_0$, Don't regularize it

The regularization term is in concrete implementation , The summation part can be written as ${\sum }_{j=1}^{n=m}{\theta }_j^2={\theta }^T\theta$, And use ${\theta }^{T}M\theta$ Instead of ${\theta }^T\theta$, matrix $M$ It's a matrix that varies according to the kernel function we choose , This can improve the computational efficiency , The modified cost function is ：
$$C\sum _{i=1}^m\left[y^{(i)}Cos{t}_1({\theta }^T{f}^{(i)})+(1-y^{(i)})Cos{t}_0({\theta }^T{f}^{(i)})\right]+\frac{1}{2}{\theta }^{T}M\theta$$

Theoretically speaking , We can also use kernel functions in logistic regression , But it uses 𝑀 The method to simplify the calculation is not suitable for logistic regression , So computing is going to be very time consuming .
　　 Here it is , We do not introduce a method to minimize the cost function of support vector machines , You can use existing packages （ Such as
liblinear,libsvm etc. ）. Before we use these packages to minimize our cost function , We usually need to write a core
function , And if we use Gaussian kernel functions , So it is necessary to scale features before using them .
　　 in addition , Support vector machines can also use no kernel function , Not using kernel function is also called linear kernel function (linear kernel),
When we don't use very complex functions , Or when we have a lot of features in our training set and very few examples , Can pick
Use this support vector machine without kernel function .
　　 Here are two parameters for SVM 𝐶 and 𝜎 Influence ：
𝐶 = 1/𝜆
𝐶 large , amount to 𝜆 smaller , May cause over fitting , High variance ;
𝐶 More hours , amount to 𝜆 more , May cause low fit , High deviation ;
𝜎 large , May lead to low variance , High deviation ;
𝜎 More hours , May cause low deviation , High variance .
come from https://www.cnblogs.com/sl0309/p/10499278.html

The above figure shows the influence of two parameters on the result

12-6 Using support vector machines (SVM)

• Use SVM Software library to calculate $\theta$ Value
• We need to choose C Value
• We need to choose kernel function
  • Linear kernel function ： Do not select kernel function , Use linear fitting directly , It can be found in the number of features n It's big , And the number of samples m Use in very small cases
  • Gaussian kernel ： It can be found in the number of samples m It's big , Number of features n Use in very small cases , It can fit the nonlinear boundary

When using nonlinear kernel function , The eigenvalues need to be normalized
The kernel function needs to satisfy the mersel theorem Mercer’s theorem