当前位置:网站首页>[set theory] inclusion exclusion principle (including examples of exclusion principle)
[set theory] inclusion exclusion principle (including examples of exclusion principle)
2022-07-03 04:09:00 【Programmer community】
List of articles
- One 、 Principle of tolerance and exclusion
- Two 、 Principle of tolerance and exclusion Example
One 、 Principle of tolerance and exclusion
A
1
,
A
2
,
⋯
,
A
n
A_1 , A_2 , \cdots , A_n
A1,A2,⋯,An yes
n
n
n A collection of ; be this
n
n
n A collection of Number of elements in union yes :
∣
⋃
i
=
1
n
A
i
∣
=
∑
i
=
1
n
∣
A
i
∣
−
∑
i
<
j
∣
A
i
∩
A
j
∣
+
∑
i
<
j
<
k
∣
A
i
∩
A
j
∩
A
k
∣
−
⋯
+
(
−
1
)
n
−
1
∣
A
1
∩
A
2
∩
⋯
∩
A
n
∣
| \bigcup_{i=1}^{n} A_i | = \sum_{i = 1}^n | A_i | - \sum_{i < j} | A_i \cap A_j | + \sum_{i < j < k} | A_i \cap A_j \cap A_k | - \cdots + ( -1 )^{n - 1} | A_1 \cap A_2 \cap \cdots \cap An |
∣i=1⋃nAi∣=i=1∑n∣Ai∣−i<j∑∣Ai∩Aj∣+i<j<k∑∣Ai∩Aj∩Ak∣−⋯+(−1)n−1∣A1∩A2∩⋯∩An∣
analysis :
n
n
n After the union operation of sets , Element number , Usually use Principle of tolerance and exclusion Calculate ;
∑
i
=
1
n
∣
A
i
∣
\sum_{i = 1}^n | A_i |
∑i=1n∣Ai∣ : In each set Element number Add up , The value is greater than Total elements , Need to be corrected ; ( Coefficient value
(
−
1
)
0
(-1)^0
(−1)0 )
∑
i
<
j
∣
A
i
∩
A
j
∣
\sum_{i < j} | A_i \cap A_j |
∑i<j∣Ai∩Aj∣ : Subtract the number of intersecting elements , This value is less than Total elements , Continue to make corrections ; ( Coefficient value
(
−
1
)
1
(-1)^1
(−1)1 )
∑
i
<
j
<
k
∣
A
i
∩
A
j
∩
A
k
∣
\sum_{i < j < k} | A_i \cap A_j \cap A_k |
∑i<j<k∣Ai∩Aj∩Ak∣ : Add the number of elements intersected by the three sets , The value is greater than Total elements , Continue to make corrections ; ( Coefficient value
(
−
1
)
2
(-1)^2
(−1)2 )
Subtract the number of elements intersected by the four sets , The value is less than Total elements , Continue to make corrections ; ( Coefficient value
(
−
1
)
3
(-1)^3
(−1)3 )
⋮
\vdots
⋮
(
−
1
)
n
−
1
∣
A
1
∩
A
2
∩
⋯
∩
A
n
∣
( -1 )^{n - 1} | A_1 \cap A_2 \cap \cdots \cap An |
(−1)n−1∣A1∩A2∩⋯∩An∣ : add
(
−
1
)
n
−
1
( -1 )^{n - 1}
(−1)n−1 multiply
n
−
1
n-1
n−1 The number of elements intersected by sets ; ( Coefficient value
(
−
1
)
n
−
1
(-1)^{n-1}
(−1)n−1 )
Above Odd sets Number of intersection elements The former coefficient is Positive numbers , Even number of sets Number of intersection elements The former coefficient is negative ;
Two 、 Principle of tolerance and exclusion Example
1
1
1 ~
10000
10000
10000 Between , It is neither the square of an integer , It's not the cube of an integer , Number of ?
The complete :
E
E
E A set is a complete set , yes
1
1
1 To
10000
10000
10000 The natural number of ,
E
E
E The number of sets
∣
E
∣
=
10000
|E| = 10000
∣E∣=10000
The set of numbers corresponding to square
A
A
A :
A
A
A A set is Some number The square of Corresponding Some number aggregate ,
A
=
{
x
∈
E
∣
x
=
k
2
∧
k
∈
Z
}
A = \{ x \in E | x = k^2 \land k \in Z \}
A={ x∈E∣x=k2∧k∈Z} ,
A
A
A The number of set elements is
∣
100
∣
|100|
∣100∣ ;
10
0
2
=
10000
100^2 = 10000
1002=10000 , therefore
A
A
A The elements of the set are
{
0
,
1
,
2
,
⋯
,
100
}
\{0, 1, 2 , \cdots , 100 \}
{ 0,1,2,⋯,100} , The number of elements is
100
100
100 individual ;
1
2
,
2
2
,
3
3
,
⋯
,
10
0
2
1^2 , 2^2 , 3^3, \cdots ,100^2
12,22,33,⋯,1002 All in
1
1
1 To
10000
10000
10000 Between ,
10
1
2
=
10201
101^2 = 10201
1012=10201 More than
10000
10000
10000 了 ;
The set of numbers corresponding to the cube
B
B
B :
B
B
B A set is Some number The cube of Corresponding Some number aggregate ,
B
=
{
x
∈
E
∣
x
=
k
3
∧
k
∈
Z
}
B = \{ x \in E | x = k^3 \land k \in Z \}
B={ x∈E∣x=k3∧k∈Z} ,
A
A
A The number of set elements is
∣
21
∣
|21|
∣21∣ ;
2
1
3
=
9261
21^3 = 9261
213=9261 , therefore
B
B
B The elements of the set are
{
0
,
1
,
2
,
⋯
,
21
}
\{0, 1, 2 , \cdots , 21 \}
{ 0,1,2,⋯,21} , The number of elements is
21
21
21 individual ;
1
3
,
2
3
,
3
3
,
⋯
,
2
1
3
1^3 , 2^3 , 3^3, \cdots ,21^3
13,23,33,⋯,213 All in
1
1
1 To
10000
10000
10000 Between ,
2
2
2
=
10648
22^2 = 10648
222=10648 More than
10000
10000
10000 了 ;
Calculation
A
∩
B
A \cap B
A∩B Intersection of sets
C
C
C : Element number , Is square , It's cubic again , It must be a number to the power of six ,
C
=
{
x
∈
E
∣
x
=
k
6
∧
k
∈
Z
}
C= \{ x \in E | x = k^6 \land k \in Z \}
C={ x∈E∣x=k6∧k∈Z} ,
C
C
C The number of elements in the set is
4
4
4 ;
4
6
=
4096
4^6 = 4096
46=4096 , therefore
C
C
C The elements of the set are
{
1
,
2
,
3
,
4
}
\{1, 2 , 3, 4\}
{ 1,2,3,4} , The number of elements is
4
4
4 individual ;
1
6
,
2
6
,
3
6
,
4
6
1^6 , 2^6 , 3^6, 4^6
16,26,36,46 All in
1
1
1 To
10000
10000
10000 Between ,
5
6
=
15
,
625
5^6 = 15,625
56=15,625 More than
10000
10000
10000 了 ;
The title can be translated into : aggregate
Z
Z
Z in , Neither belong to
A
A
A aggregate , Have not belong to
B
B
B aggregate The number of ;
aggregate
A
A
A And aggregate
B
B
B Union is
A
∪
B
A \cup B
A∪B
The above union Of Absolute complement
∼
(
A
∪
B
)
\sim ( A \cup B )
∼(A∪B) Element number
∣
∼
(
A
∪
B
)
∣
|\sim ( A \cup B ) |
∣∼(A∪B)∣ , It is the result required in the title ;
∣
∼
(
A
∪
B
)
∣
=
∣
E
∣
−
∣
A
∪
B
∣
|\sim ( A \cup B ) | = |E| - |A \cup B|
∣∼(A∪B)∣=∣E∣−∣A∪B∣
In the above formula ,
∣
E
∣
=
10000
|E| = 10000
∣E∣=10000 ,
∣
A
∪
B
∣
|A \cup B|
∣A∪B∣ Value can be used Principle of tolerance and exclusion Calculate ;
∣
A
∪
B
∣
|A \cup B|
∣A∪B∣ The number of elements of the union of two sets , You can add the number of elements of two sets , Then subtract the number of elements of the intersection of two sets ;
∣
A
∪
B
∣
=
∣
A
∣
+
∣
B
∣
−
∣
A
∪
B
∣
=
100
+
21
−
4
=
117
|A \cup B| = |A| + |B| - |A \cup B| = 100 + 21 - 4 = 117
∣A∪B∣=∣A∣+∣B∣−∣A∪B∣=100+21−4=117
Substitute into the general formula :
∣
∼
(
A
∪
B
)
∣
=
∣
E
∣
−
∣
A
∪
B
∣
=
10000
−
117
=
9883
|\sim ( A \cup B ) | = |E| - |A \cup B| = 10000 - 117 = 9883
∣∼(A∪B)∣=∣E∣−∣A∪B∣=10000−117=9883
边栏推荐
- DAPP for getting started with eth
- 2022 P cylinder filling examination content and P cylinder filling practice examination video
- China Mobile Internet of things oneos and onenet were selected in the list of 2021 Internet of things demonstration projects
- Pdf editing tool movavi pdfchef 2022 direct download
- What can learning pytorch do?
- Mila, University of Ottawa | molecular geometry pre training with Se (3) invariant denoising distance matching
- Basic MySQL operations
- Mila、渥太华大学 | 用SE(3)不变去噪距离匹配进行分子几何预训练
- 300+篇文献!一文详解基于Transformer的多模态学习最新进展
- Is pytorch difficult to learn? How to learn pytorch well?
猜你喜欢
![[brush questions] find the number pair distance with the smallest K](/img/e1/4118e2b37b5cea0454d65b877b507f.png)
[brush questions] find the number pair distance with the smallest K

What can learning pytorch do?

JS native common knowledge

Application of I2C protocol of STM32F103 (read and write EEPROM)

Appium自动化测试框架

Feature_selection
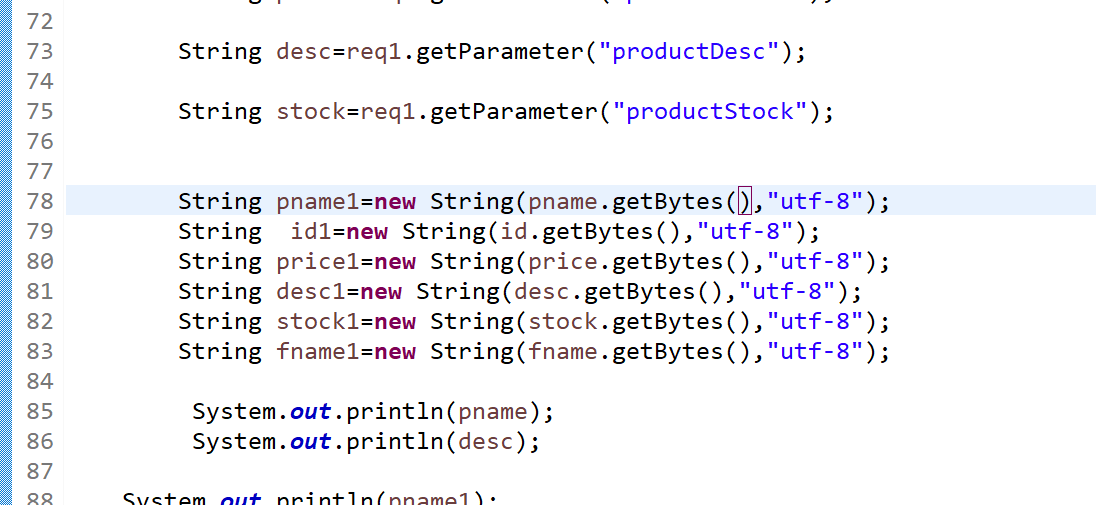
在写web项目的时候,文件上传用到了smartupload,用了new string()进行转码,但是在数据库中,还是会出现类似扑克的乱码
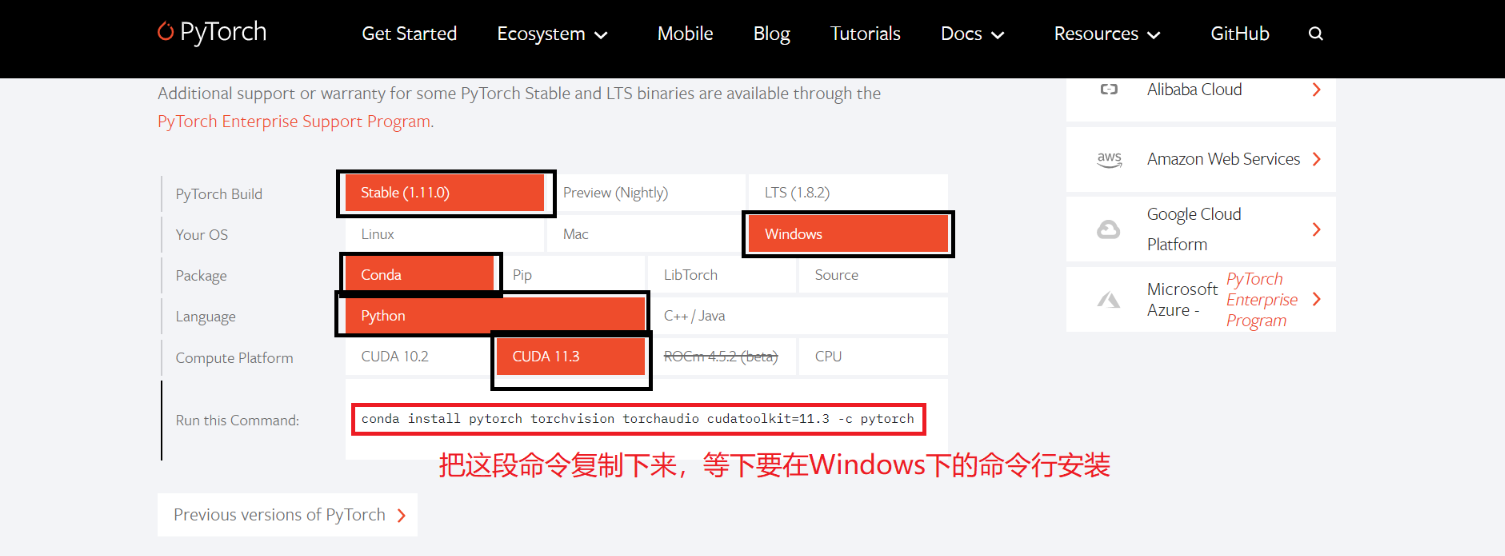
pytorch怎么下载?pytorch在哪里下载?

【毕业季·进击的技术er】职场人的自白
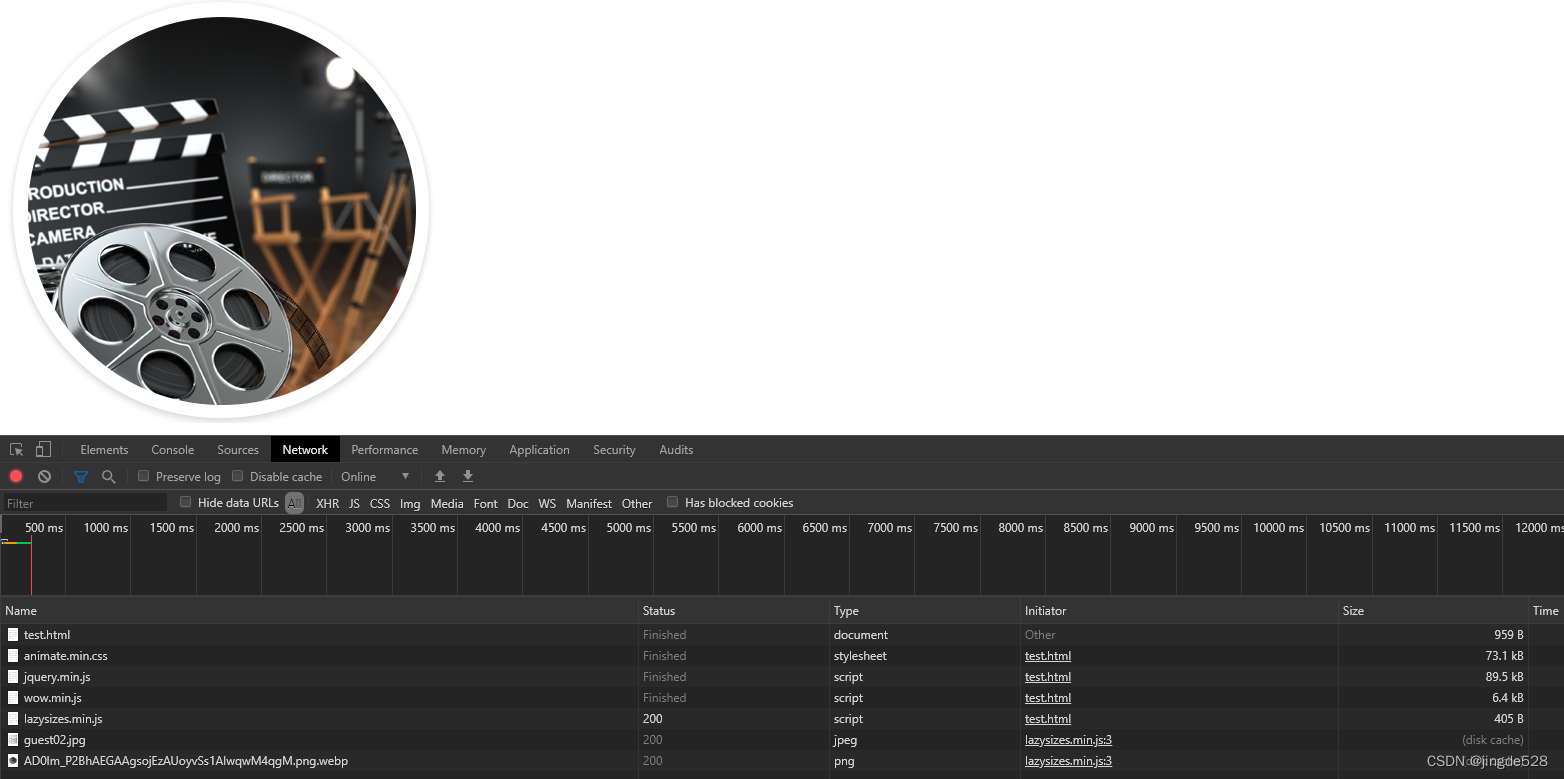
js实现在可视区内,文字图片动画效果
随机推荐
Appium automated testing framework
Is it better to speculate in the short term or the medium and long term? Comparative analysis of differences
Makefile demo
在 .NET 6 项目中使用 Startup.cs
[no title] 2022 chlorination process examination content and free chlorination process examination questions
[brush questions] connected with rainwater (one dimension)
[set theory] set concept and relationship (set represents | number set | set relationship | contains | equality | set relationship property)
nodejs基础:浅聊url和querystring模块
2022 tea master (intermediate) examination questions and analysis and tea master (intermediate) practical examination video
Nat. Comm. | 使用Tensor-cell2cell对细胞通讯进行环境感知去卷积
Intercept string fixed length to array
[graduation season · aggressive technology Er] Confessions of workers
Arduino application development - LCD display GIF dynamic diagram
Idea shortcut keys
Basic syntax of class
The time has come for the domestic PC system to complete the closed loop and replace the American software and hardware system
[daily question] dichotomy - find a single dog (Bushi)
JS native common knowledge
Is pytorch open source?
CVPR 2022 | Dalian Technology propose un cadre d'éclairage auto - étalonné pour l'amélioration de l'image de faible luminosité de la scène réelle