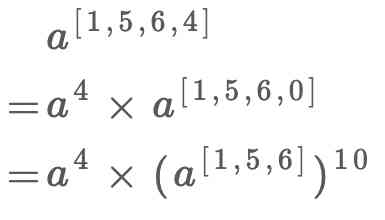After reading this article , You can go and get the following questions :
-----------
One 、 What is? LRU Algorithm
It's a cache elimination strategy .
The cache capacity of the computer is limited , If the cache is full, delete some content , Make room for new content . But the problem is , What should I delete ? We certainly want to delete useless caches , And keep the useful data in the cache , Continue to use after convenience . that , What kind of data , We decided that 「 Helpful 」 What about the data? ?
LRU Cache elimination algorithm is a common strategy .LRU The full name is Least Recently Used, In other words, we think that the data used recently should be 「 Helpful 」, Data that hasn't been used for a long time should be useless , When the memory is full, the priority is to delete the data that has not been used for a long time .
PS: I've seriously written about 100 Multiple original articles , Hand brush 200 Daoli is the subject , All published in labuladong A copy of the algorithm , Continuous updating . Recommended collection , Write the title in the order of my article , Master all kinds of algorithm set, then put into the sea of questions, like fish .
A simple example , Android phones can put software in the background to run , For example, I opened it one after another 「 Set up 」「 Cell phone manager 」「 The calendar 」, So now they are in this order in the background :
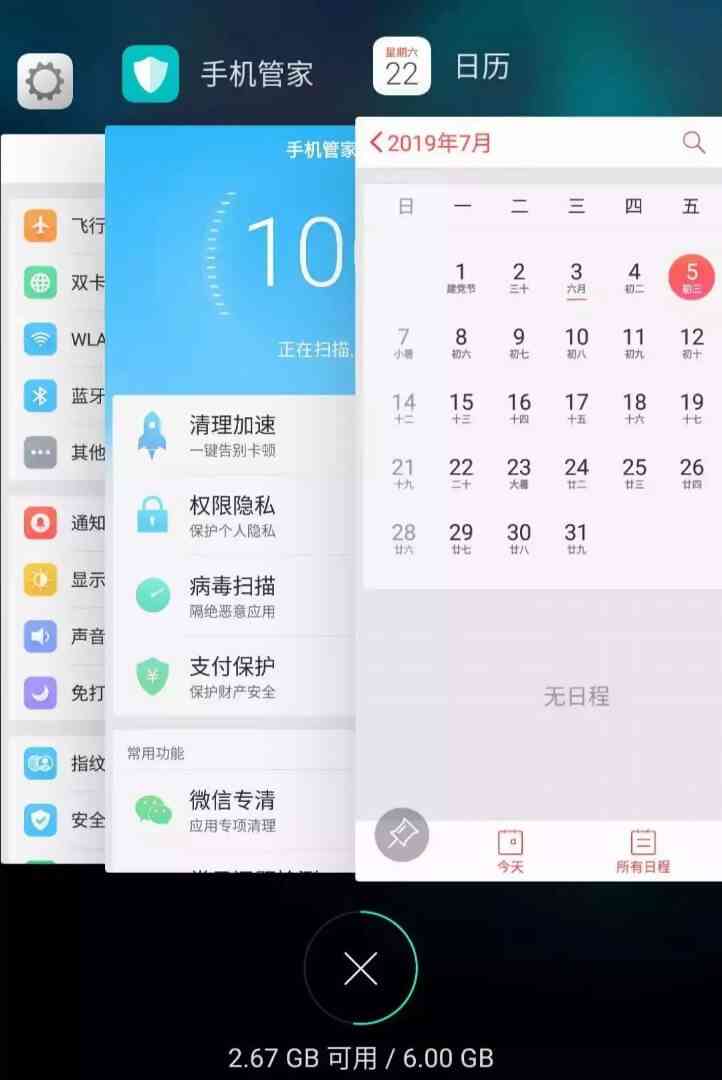
But at this time if I visit 「 Set up 」 Interface , that 「 Set up 」 Will be advanced to the first , It's like this :
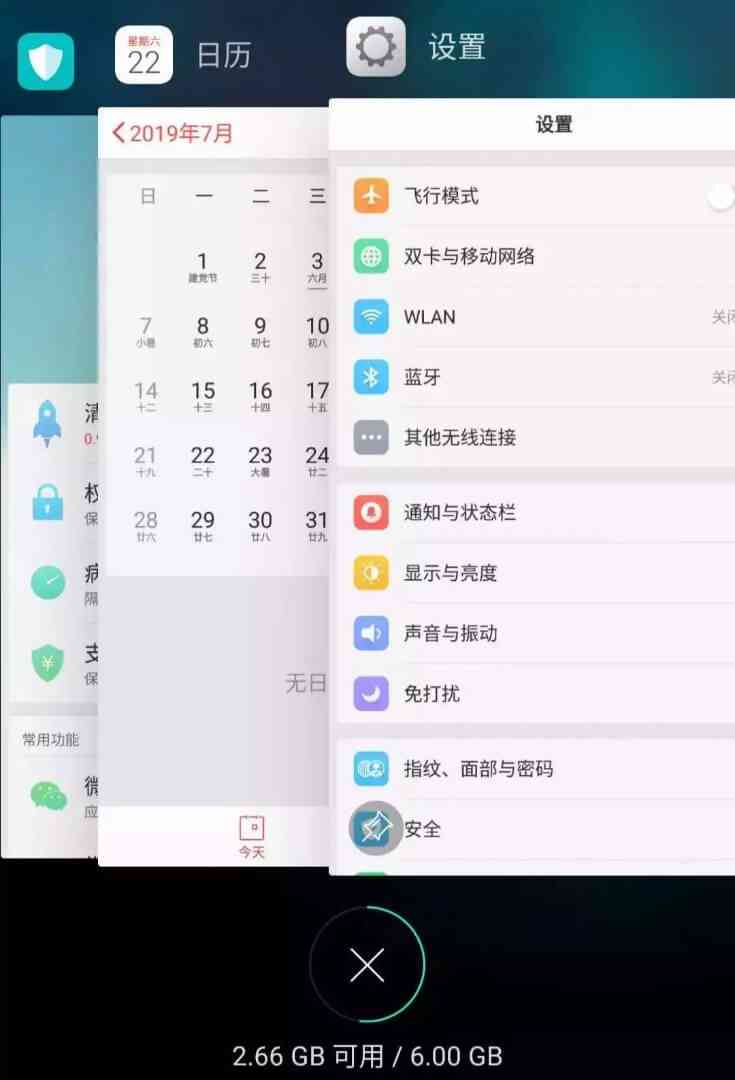
Suppose my phone only allows me to turn on at the same time 3 Applications , It's full now . So if I open a new app 「 The clock 」, You have to close an app for 「 The clock 」 Make a place , How about that one ?
according to LRU The strategy of , Close the bottom 「 Cell phone manager 」, Because it's the longest unused , Then put the new app on top :
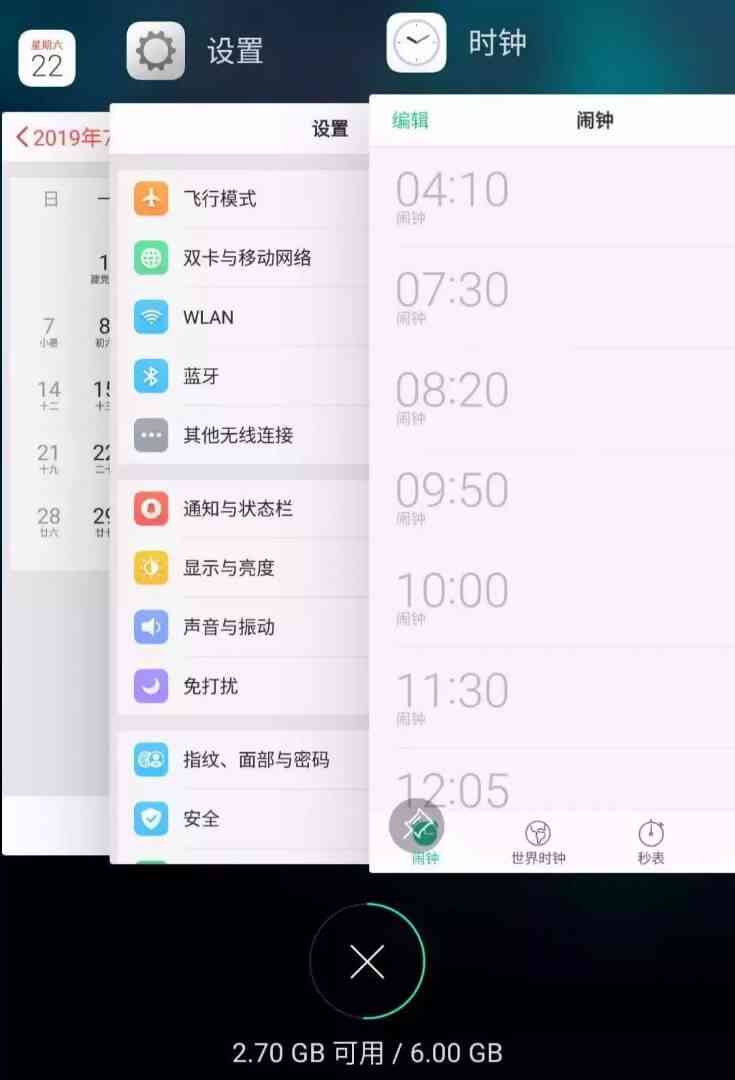
Now you should understand LRU(Least Recently Used) Strategy . Of course, there are other cache elimination strategies , For example, don't eliminate them according to the visiting time sequence , But according to the frequency of visits (LFU Strategy ) To eliminate and so on , There are different application scenarios . This article explains LRU Algorithm strategy .
PS: I've seriously written about 100 Multiple original articles , Hand brush 200 Daoli is the subject , All published in labuladong A copy of the algorithm , Continuous updating . Recommended collection , Write the title in the order of my article , Master all kinds of algorithm set, then put into the sea of questions, like fish .
Two 、LRU Algorithm description
LRU Algorithms actually let you design data structures : The first thing to do is to receive a capacity Parameter as the maximum capacity of the cache , Then realize two API, One is put(key, val) Method to store key value pairs , The other is get(key) Method to get key Corresponding val, If key Returns if it does not exist -1.
Watch out! ,get and put The methods must all be O(1) Time complexity of , Let's take a concrete example to see LRU How does the algorithm work .
/* The cache capacity is 2 */
LRUCache cache = new LRUCache(2);
// You can take cache Understand it as a line
// Let's say the team leader is on the left , On the right is the end of the team
// The most recent one is at the head of the line , The unused ones are at the end of the line
// Parentheses indicate key value pairs (key, val)
cache.put(1, 1);
// cache = [(1, 1)]
cache.put(2, 2);
// cache = [(2, 2), (1, 1)]
cache.get(1); // return 1
// cache = [(1, 1), (2, 2)]
// explain : Because recently I visited the key 1, So get ahead of the team
// Return key 1 Corresponding value 1
cache.put(3, 3);
// cache = [(3, 3), (1, 1)]
// explain : The cache capacity is full , Need to delete content empty location
// Priority to delete unused data , That's the data at the end of the team
// Then insert the new data into the team head
cache.get(2); // return -1 ( Not found )
// cache = [(3, 3), (1, 1)]
// explain :cache There is no key in 2 The data of
cache.put(1, 4);
// cache = [(1, 4), (3, 3)]
// explain : key 1 Already exists , Put the original value 1 Overlay as 4
// Don't forget to also advance the key value pair to the team leader
3、 ... and 、LRU Algorithm design
Analyze the above operation process , Must let put and get The time complexity of the method is O(1), We can conclude that cache The necessary conditions for this data structure : Quick search , Insert fast , Delete fast , There is order .
Because obviously cache There must be order , To distinguish between recently used and long unused data ; And we're going to be in cache Whether the search key already exists in ; If the capacity is full, delete the last data ; Every time you visit, you have to insert the data into the team head .
that , What data structure meets the above conditions at the same time ? Fast hash table lookup , But there is no fixed order of data ; There are order in the list , Insert delete fast , But search is slow . So combine , Form a new data structure : Hash list .
LRU The core data structure of cache algorithm is Hash list , A combination of a two-way linked list and a hash table . This data structure is so long :
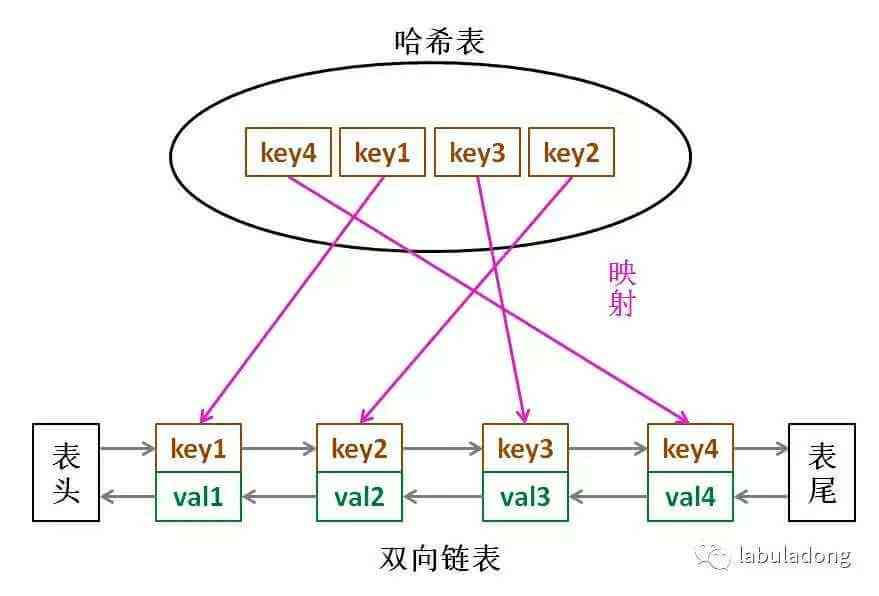
The idea is simple , With the help of hash table, it gives a fast lookup feature to linked list : You can quickly find a key Is there a cache ( Linked list ) in , At the same time, it can be deleted quickly 、 Add a node . Think back to the example , Is this data structure a perfect solution LRU The need for caching ?
Perhaps the reader will ask , Why is it a double linked list , A single chain watch will do ? in addition , Now that the hash table has been saved key, Why should key value pairs be stored in the linked list , Just save the value ?
When you think about it, it's all a question , Only when it's done can there be an answer . The reason for the design , It must wait for us to realize LRU Only after the algorithm can we understand , So let's start looking at the code ~
Four 、 Code implementation
Many programming languages have built-in hash lists or the like LRU Library functions for functions , But to help you understand the details of the algorithm , We use it Java Make your own wheels and do it again LRU Algorithm .
First , Let's write out the node class of the double linked list , In order to simplify the ,key and val All considered to be int type :
class Node {
public int key, val;
public Node next, prev;
public Node(int k, int v) {
this.key = k;
this.val = v;
}
}
And then rely on our Node Type to build a double linked list , Achieve a few needed API( The time complexity of these operations is O(1)):
class DoubleList {
// Add nodes to the head of the list x, Time O(1)
public void addFirst(Node x);
// Delete... From the list x node (x There must be )
// Because it's a double linked list and gives you the target Node node , Time O(1)
public void remove(Node x);
// Delete the last node in the list , And return the node , Time O(1)
public Node removeLast();
// Return the length of the list , Time O(1)
public int size();
}
PS: This is the realization of the common two-way linked list , To keep the reader focused on understanding LRU The logic of the algorithm , Omit the specific code of the linked list .
Here we can answer the question just now “ Why do we have to use double linked list ” The problem. , Because we need to delete operations . Deleting a node requires not only a pointer to the node itself , You also need to operate the pointer of its predecessor node , And the two-way linked list can support the direct search of the precursor , Ensure the time complexity of operation O(1).
PS: I've seriously written about 100 Multiple original articles , Hand brush 200 Daoli is the subject , All published in labuladong A copy of the algorithm , Continuous updating . Recommended collection , Write the title in the order of my article , Master all kinds of algorithm set, then put into the sea of questions, like fish .
With the realization of two-way linked list , All we need to do is LRU In the algorithm, it can be combined with hash table . Let's make the logic clear :
// key Mapping to Node(key, val)
HashMap<Integer, Node> map;
// Node(k1, v1) <-> Node(k2, v2)...
DoubleList cache;
int get(int key) {
if (key non-existent ) {
return -1;
} else {
Put the data (key, val) Mention the beginning ;
return val;
}
}
void put(int key, int val) {
Node x = new Node(key, val);
if (key Already exists ) {
Delete old data ;
New nodes x Insert at the beginning ;
} else {
if (cache Is full ) {
Delete the last data in the linked list ;
Delete map The key mapped to the data in the ;
}
New nodes x Insert at the beginning ;
map New China key For new nodes x Mapping ;
}
}
If you can understand the above logic , It's easy to understand when translated into code :
class LRUCache {
// key -> Node(key, val)
private HashMap<Integer, Node> map;
// Node(k1, v1) <-> Node(k2, v2)...
private DoubleList cache;
// The maximum capacity
private int cap;
public LRUCache(int capacity) {
this.cap = capacity;
map = new HashMap<>();
cache = new DoubleList();
}
public int get(int key) {
if (!map.containsKey(key))
return -1;
int val = map.get(key).val;
// utilize put Method to advance the data
put(key, val);
return val;
}
public void put(int key, int val) {
// First put the new node x Make it out
Node x = new Node(key, val);
if (map.containsKey(key)) {
// Delete old nodes , A new one in the head
cache.remove(map.get(key));
cache.addFirst(x);
// to update map The corresponding data in
map.put(key, x);
} else {
if (cap == cache.size()) {
// Delete the last data in the linked list
Node last = cache.removeLast();
map.remove(last.key);
}
// Add directly to the head
cache.addFirst(x);
map.put(key, x);
}
}
}
Here you can answer the previous question “ Why store in linked list at the same time key and val, Instead of just storing val”, Notice this code :
if (cap == cache.size()) {
// Delete the last data in the linked list
Node last = cache.removeLast();
map.remove(last.key);
}
When the cache capacity is full , We don't just delete the last one Node node , And map Mapping to this node key At the same time to delete , And this key Only by Node obtain . If Node Only store... In the structure val, Then we won't know key What is it? , Can't delete map The key , Cause mistakes .
thus , You should have mastered LRU The idea and implementation of the algorithm , It's easy to make mistakes : Do not forget to update the mapping of nodes in the hash table while processing the linked list nodes .
_____________
my Online e-books Yes 100 Original articles , Hands with brushes 200 Daoli is the subject , Recommended collection ! Corresponding GitHub Algorithm Repository We've got it 70k star, Welcome to mark star !