当前位置:网站首页>(五)栈及其应用
(五)栈及其应用
2022-08-04 05:28:00 【顺毛黑起】
数据结构–栈
1.栈是一个先进后出的有序列表2.栈(stack)限制了只能在线性表的同一端进行操作。允许插入和删除的一端为变化的一端,称为栈顶(top),另一端为固定的一端,称为栈底(bottom)
入栈(push)示意图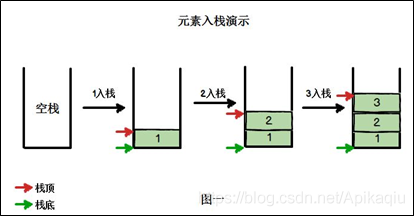 出栈(pop)示意图
出栈(pop)示意图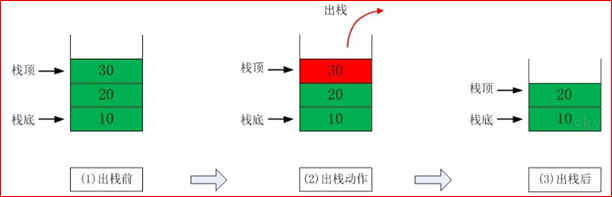
栈的应用场景
数组模拟栈
思路分析图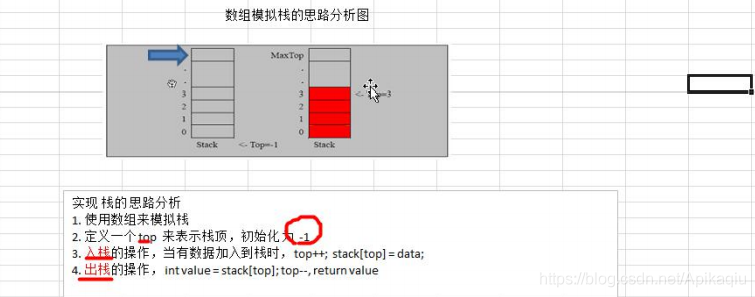
package com.atguigu.stack;
import java.util.Scanner;
public class ArrayStackDemo {
public static void main(String[] args) {
ArrayStack stack=new ArrayStack(4);
String key="";
boolean loop=true;//控制是否退出菜单
Scanner scanner = new Scanner(System.in);
while (loop){
System.out.println("show:表示显示栈");
System.out.println("exit:退出程序");
System.out.println("push:入栈");
System.out.println("pop:出栈");
System.out.println("请输入");
key=scanner.next();
switch (key){
case "show":
stack.list();
break;
case "push":
System.out.println("请输入数字:");
int value=scanner.nextInt();
stack.push(value);
break;
case "pop":
try{
int res=stack.pop();
System.out.printf("出栈的数据是%d\n",res);
}catch (Exception e){
System.out.println(e.getMessage());
}
break;
case "exit":
scanner.close();
loop=false;
break;
default:
break;
}
}
System.out.println("程序退出~~~");
}
}
class ArrayStack{
private int maxSize;//栈的大小
private int[] stack;//数组,数组模拟栈
private int top=-1;//top表示栈顶,初始化为-1
//构造器
public ArrayStack(int maxSize){
this.maxSize=maxSize;
stack=new int[this.maxSize];
}
//栈满
public boolean isFull(){
return top==maxSize-1;
}
//栈空
public boolean isEmpty(){
return top==-1;
}
//入栈push
public void push(int value){
if (isFull()){
System.out.println("栈满");
return;
}
top++;
stack[top]=value;
}
//出栈pop,将栈顶元素返回
public int pop(){
if (isEmpty()){
//抛出异常
throw new RuntimeException("栈空,没有数据");
}
int value=stack[top];
top--;
return value;
}
//遍历栈
public void list(){
if (isEmpty()){
System.out.println("栈空,没有数据~~");
return;
}
for (int i = top; i >=0 ; i--) {
System.out.printf("stack[%d]=%d\n",i,stack[i]);
}
}
}
栈的应用
栈实现综合计算器

package com.atguigu.stack;
public class Calculator {
public static void main(String[] args) {
String expression="70+2*6-2";
//先创建两个栈,数栈和符号栈
ArrayStack2 numStack = new ArrayStack2(10);
ArrayStack2 operStack = new ArrayStack2(10);
//定义需要的相关变量
int index=0;//用于扫描
int num1=0;
int num2=0;
int oper=0;
int res=0;
char ch=' ';//将每次扫描得到的char保存到ch中
String keepNum="";//用于拼接多位数
while (true){
//依次得到expression的每一个字符
ch=expression.substring(index,index+1).charAt(0);
//判断
if (operStack.isOper(ch)){
//判断当前符号栈是否为空
if (!operStack.isEmpty()){
//处理
if (operStack.priority(ch)<=operStack.priority(operStack.peek())){
num1=numStack.pop();
num2=numStack.pop();
oper=operStack.pop();
res=numStack.cal(num1,num2,oper);
//运算的结果入数栈
numStack.push(res);
//当前运算符入符号栈
operStack.push(ch);
}else {
operStack.push(ch);
}
}else {
//为空则直接入栈
operStack.push(ch);
}
}else {
//如果是数
// numStack.push(ch-48); //注意数字对应的ascall码
/** * 当处理多位数时,不能发现是一个数就立即入栈,因为它可能是多位数 * 在处理数时,需要向expression的表达式的index后再看一位,如果是符号才入栈 * 因此需要定义一个字符串变量,用于拼接 */
keepNum+=ch;
//如果ch是expression的最后一位。就直接入栈
if (index==expression.length()-1){
numStack.push(Integer.parseInt(keepNum));
}else {
//判断下一个字符是不是数字,如果是数字继续扫描,否则入栈
if (operStack.isOper(expression.substring(index+1,index+2).charAt(0))){
//如果后一位是操作符,则入栈keepNum="1"或者"123"
numStack.push(Integer.parseInt(keepNum));
//注意:keepNum清空
keepNum="";
}
}
}
//让index+1,并判断是否扫描到expression最后
index++;
if (index>=expression.length()){
break;
}
}
//当表达式扫描完毕,顺序从数栈和符号栈中pop出相应的数和符号,进行运算
while (true){
//如果符号栈为空,则计算到最后的结果,数栈中只有一个结果
if (operStack.isEmpty()){
break;
}
num1=numStack.pop();
num2=numStack.pop();
oper=operStack.pop();
res=numStack.cal(num1,num2,oper);
//运算的结果入数栈
numStack.push(res);
}
int res2=numStack.pop();
System.out.printf("表达式%s=%d",expression,res2);
}
}
class ArrayStack2{
private int maxSize;//栈的大小
private int[] stack;//数组,数组模拟栈
private int top=-1;//top表示栈顶,初始化为-1
//构造器
public ArrayStack2(int maxSize){
this.maxSize=maxSize;
stack=new int[this.maxSize];
}
//返回当前栈顶元素
public int peek(){
return stack[top];
}
//栈满
public boolean isFull(){
return top==maxSize-1;
}
//栈空
public boolean isEmpty(){
return top==-1;
}
//入栈push
public void push(int value){
if (isFull()){
System.out.println("栈满");
return;
}
top++;
stack[top]=value;
}
//出栈pop,将栈顶元素返回
public int pop(){
if (isEmpty()){
//抛出异常
throw new RuntimeException("栈空,没有数据");
}
int value=stack[top];
top--;
return value;
}
//遍历栈
public void list(){
if (isEmpty()){
System.out.println("栈空,没有数据~~");
return;
}
for (int i = top; i >=0 ; i--) {
System.out.printf("stack[%d]=%d\n",i,stack[i]);
}
}
//返回自定义的运算符优先级 优先级使用数字表示,数字越大,优先级越高
public int priority(int oper){
if (oper=='*'||oper=='/'){
return 1;
}else if (oper=='+' || oper=='-'){
return 0;
}else {
return -1;
}
}
//判断是不是运算符
public boolean isOper(char val){
return val=='+'|| val=='-'|| val=='*'|| val=='/';
}
//计算方法
public int cal(int num1,int num2,int oper){
int res=0;
switch (oper){
case '+':
res=num1+num2;
break;
case '-':
res=num2-num1;//后弹出的数字作为被减数
break;
case '*':
res=num1*num2;
break;
case '/':
res=num2/num1;
break;
default:
break;
}
return res;
}
}
前缀表达式(波兰表达式)、中缀表达式以及后缀表达式(逆波兰表达式)
前缀表达式的运算符位于操作数之前




package com.atguigu.stack;
import java.util.ArrayList;
import java.util.List;
import java.util.Stack;
public class PolandNotation {
public static void main(String[] args) {
//先定义一个逆波兰表达式
//(3+4)*5-6 => 3 4 + 5 * 6 -
String suffixExpression="3 4 + 5 * 6 -";//字符串中间使用空格隔开
/** * 1.先将"3 4 + 5 * 6 - "放入到ArrayList中 * 2.将ArrayList传递给一个方法,遍历ArrayList配合栈完成计算 */
List<String> rpnList=getListString(suffixExpression);
System.out.println("rpnList="+rpnList);
int res=calculate(rpnList);
System.out.println("计算的结果是="+res);
}
//将一个逆波兰表达式依次将数据和运算符放入到ArrayList中
public static List<String> getListString(String suffixExpression){
String[] split = suffixExpression.split(" ");
List<String> list=new ArrayList<>();
for (String ele:split) {
list.add(ele);
}
return list;
}
//完成对逆波兰表达式的运算
public static int calculate(List<String> ls){
//创建栈
Stack<String> stack = new Stack<>();
//遍历ls
for (String item:ls) {
//这里使用正则表达式取出数
if (item.matches("\\d+")){
//匹配的是多位数
//入栈
stack.push(item);
}else {
//pop出两个数并运算,再入栈
int num2=Integer.parseInt(stack.pop());//字符串转整数
int num1=Integer.parseInt(stack.pop());
int res=0;
if (item.equals("+")){
res=num1+num2;
}else if (item.equals("-")){
res=num1-num2;
}else if (item.equals("*")){
res=num1*num2;
}else if (item.equals("/")){
res=num1/num2;
}else {
throw new RuntimeException("运算符有误");
}
stack.push(""+res);//注意入栈的是字符串,所以整数res拼接""转成字符串
}
}
//最后留在stack中的数据就是运算结果
return Integer.parseInt(stack.pop());
}
}
中缀表达式转换成后缀表达式
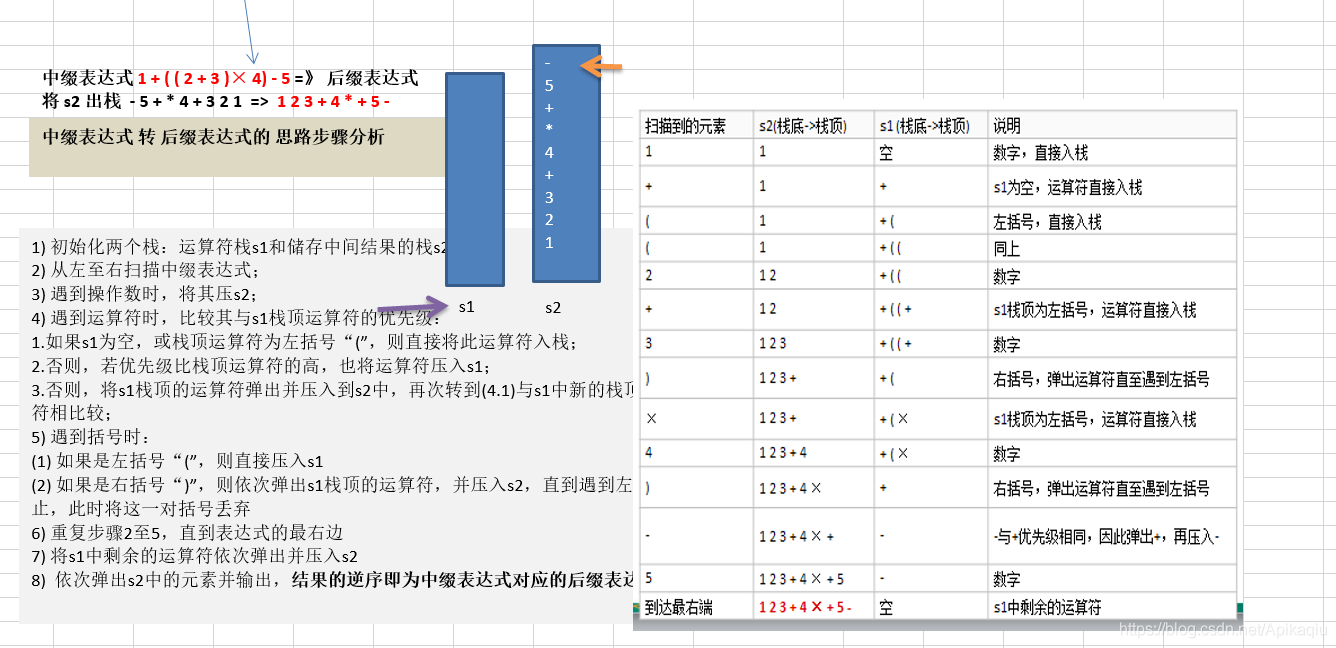
1.具体步骤
- 初始化两个栈:运算符栈 s1 和储存中间结果的栈 s2;
- 从左至右扫描中缀表达式;
- 遇到操作数时,将其压 s2;
- 遇到运算符时,比较其与 s1 栈顶运算符的优先级:
1.如果 s1 为空,或栈顶运算符为左括号“(”,则直接将此运算符入栈;
2.否则,若优先级比栈顶运算符的高,也将运算符压入 s1;
3.否则,将 s1 栈顶的运算符弹出并压入到 s2 中,再次转到(4-1)与 s1 中新的栈顶运算符相比较;
5) 遇到括号时:
(1) 如果是左括号“(”,则直接压入 s1
(2) 如果是右括号“)”,则依次弹出 s1 栈顶的运算符,并压入 s2,直到遇到左括号为止,此时将这一对括号丢弃
6) 重复步骤 2 至 5,直到表达式的最右边
7) 将 s1 中剩余的运算符依次弹出并压入 s2
8) 依次弹出 s2 中的元素并输出,结果的逆序即为中缀表达式对应的后缀表达式
将中缀表达式“1+((2+3)×4)-5”转换为后缀表达式的结果为 :“1 2 3 + 4 × + 5 –”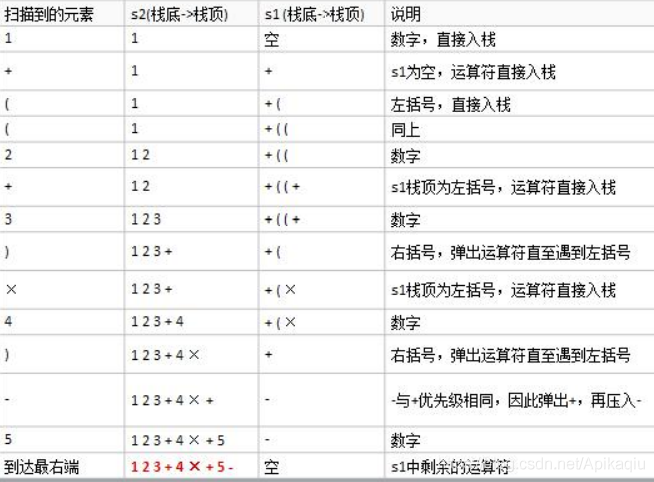
package com.atguigu.stack;
import java.util.*;
public class PolandNotation {
public static void main(String[] args) {
/** * 完成将一个中缀表达式转成后缀表达式 * 说明 * 1. 1+((2+3)x4)-5 ==> 1 2 3 + 4 * + 5 - * 2.因为直接对str进行操作不方便,因此先将"1+((2+3)x4)-5" =>中缀表达式对应的List * 3.将得到的中缀表达式对应的List ==> 后缀表达式对应的List */
String expression="1+((2+3)*4)-5";
List<String> infixExpressionList=toInfixExpressionList(expression);
System.out.println("中缀表达式对应的List="+infixExpressionList);//ArrayList [1,+,(,(,2,+,3,),*,4,),-,5]
List<String> parseSuffixExpressionList = parseSuffixExpressionList(infixExpressionList);
System.out.println("后缀表达式对应的List="+parseSuffixExpressionList);
System.out.printf("expression=%d",calculate(parseSuffixExpressionList));
/* //先定义一个逆波兰表达式 //(3+4)*5-6 => 3 4 + 5 * 6 - String suffixExpression="3 4 + 5 * 6 -";//字符串中间使用空格隔开 /** * 1.先将"3 4 + 5 * 6 - "放入到ArrayList中 * 2.将ArrayList传递给一个方法,遍历ArrayList配合栈完成计算 */
/* List<String> rpnList=getListString(suffixExpression); System.out.println("rpnList="+rpnList); int res=calculate(rpnList); System.out.println("计算的结果是="+res); */
}
//将得到的中缀表达式对应的List ==> 后缀表达式对应的List
public static List<String> parseSuffixExpressionList(List<String> ls){
//定义两个栈
Stack<String>s1=new Stack<>();//符号栈
//说明:因为s2这个栈,在整个转换的过程中,没有pop操作,而且需要逆序输出
//因此比较麻烦,这里不用Stack<String>,直接使用List<String>
//Stack<String>s2=new Stack<>();//存储中间结果的栈
List<String> s2=new ArrayList<>();//存储中间结果的Lists2
//遍历ls
for (String item:ls){
//如果是一个数,加入s2
if (item.matches("\\d+")){
s2.add(item);
}else if (item.equals("(")){
s1.push(item);
}else if (item.equals(")")){
while (!s1.peek().equals("(")){
s2.add(s1.pop());
}
s1.pop();//!!!将"("弹出s1栈,消除小括号
}else {
//当item的优先级小于等于s1栈顶运算符的优先级,将s1栈顶的运算符弹出并加入到s2中,继续与s1新的栈顶元素比较
while (s1.size()!=0 && Operation.getValue(s1.peek())>=Operation.getValue(item)){
s2.add(s1.pop());
}
//还需要将item压入栈
s1.push(item);
}
}
//将s1中剩余的运算符依次弹出并加入s2
while (s1.size()!=0){
s2.add(s1.pop());
}
return s2;//因为存放到的是List,因此按顺序输出就是对应的后缀表达式
}
//方法:将中缀表达式转成对应的List
public static List<String> toInfixExpressionList(String s){
//定义一个List,存放中缀表达式对应的内容
List<String> ls=new ArrayList<>();
int i=0;//相当于一个指针,用于遍历中缀表达式字符串
String str;//对多位数的拼接
char c;//每遍历到一个字符,就放到c中
do {
//如果c是非数字,需要加入到ls中
if (((c=s.charAt(i))<48)||((c=s.charAt(i))>57)){
ls.add(""+c);
i++;
}else {
//如果是一个数字,需要考虑多位数
str="";//先将str置空
while ((i<s.length()&&(c=s.charAt(i))>=48) && (s.charAt(i))<=57){
str+=c;//拼接
i++;
}
ls.add(str);
}
}while (i<s.length());
return ls;
}
//将一个逆波兰表达式依次将数据和运算符放入到ArrayList中
public static List<String> getListString(String suffixExpression){
String[] split = suffixExpression.split(" ");
List<String> list=new ArrayList<>();
for (String ele:split) {
list.add(ele);
}
return list;
}
//完成对逆波兰表达式的运算
public static int calculate(List<String> ls){
//创建栈
Stack<String> stack = new Stack<>();
//遍历ls
for (String item:ls) {
//这里使用正则表达式取出数
if (item.matches("\\d+")){
//匹配的是多位数
//入栈
stack.push(item);
}else {
//pop出两个数并运算,再入栈
int num2=Integer.parseInt(stack.pop());//字符串转整数
int num1=Integer.parseInt(stack.pop());
int res=0;
if (item.equals("+")){
res=num1+num2;
}else if (item.equals("-")){
res=num1-num2;
}else if (item.equals("*")){
res=num1*num2;
}else if (item.equals("/")){
res=num1/num2;
}else {
throw new RuntimeException("运算符有误");
}
stack.push(""+res);//注意入栈的是字符串,所以整数res拼接""转成字符串
}
}
//最后留在stack中的数据就是运算结果
return Integer.parseInt(stack.pop());
}
}
//Operation类,可以返回一个运算符对应的优先级
class Operation{
private static int ADD=1;
private static int SUB=1;
private static int MUL=2;
private static int DIV=2;
//写一个方法,返回对应的优先级数字
public static int getValue(String operation){
int result=0;
switch (operation){
case "+":
result=ADD;
break;
case "-":
result=SUB;
break;
case "*":
result=MUL;
break;
case "/":
result=DIV;
break;
default:
System.out.println("不存在该运算符");
break;
}
return result;
}
}
边栏推荐
猜你喜欢
随机推荐
自动化运维工具Ansible(4)变量
flink-sql所有数据类型
关系型数据库-MySQL:约束管理、索引管理、键管理语句
Kubernetes基本入门-元数据资源(四)
npm install dependency error npm ERR! code ENOTFOUNDnpm ERR! syscall getaddrinfonpm ERR! errno ENOTFOUND
webtrc 中VideoAdapter类中的作用及局限
flink-sql自定义函数
Shell(3)条件控制语句
数据库根据提纲复习
SQL练习 2022/7/5
EPSON RC+ 7.0 使用记录一
强制结束进程
flink-sql所有表连接器
lmxcms1.4
flink问题整理
k3s-轻量级Kubernetes
关系型数据库-MySQL:错误日志(log_error)
实际开发中,客户要求密码输入框禁止粘贴~
【树 图 科 技 头 条】2022年6月27日 星期一 今年ETH2.0无望
bind和function