Matlab foundation 04 - detailed analysis of the use and complex application of colon operator ":"

Preface ：

The colon is one of the most useful operators in MATLAB. It can create vectors, subscript arrays, and specify for iterations.

The colon is in Matlab Vector and array subscripts and for Iteration, etc , When making subscript expression , It is rather obscure and difficult to understand. It is necessary to discuss it separately ：

---

1 expression ：

x = j:k
x = j:i:k
A(:,n)
A(m,:)
A(:)
A(j:k)

1.1 x = j:k 【 Default interval 1,j For the first dimension ,k For the second dimension 】

 creates a unit-spaced vector x with elements [j,j+1,j+2,...,j+m] where m = fix(k-j). If j and k are both integers, then this is simply [j,j+1,...,k].

Create one with j To j+m Of Unit interval vector , The default increment step for each element is 1.

 【 case , The default interval increment step is 1, Now 】

 【 example 1】 Create a unit interval vector ：

x = 1:10
x = 1×10

     1     2     3     4     5     6     7     8     9    10

>> y=7:14

y =

     7     8     9    10    11    12    13    14

 1.2 x = j:i:k Create a vector with a specified interval

 x = j:i:k creates a regularly-spaced vector x using i as the increment between elements. The vector elements are roughly equal to [j,j+i,j+2*i,...,j+m*i] where m = fix((k-j)/i). However, if i is not an integer, then floating point arithmetic plays a role in determining whether colon includes the endpoint k in the vector, since k might not be exactly equal to j+m*i. If you specify nonscalar arrays, then MATLAB interprets j:i:k as j(1):i(1):k(1).

Create a vector of normal intervals , take i Step size added as an element .

【 example 2】 Create a vector with a specified interval ： In this example, the step size is 0.1, such 0 After starting the calculation , It happens to have

 Create vectors that increment or decrement by a specified value.

Create a vector whose elements increment by 0.1.

>> x = 0:0.1:1

x =

   Column  1  to  6

         0    0.1000    0.2000    0.3000    0.4000    0.5000

   Column  7  to  11

    0.6000    0.7000    0.8000    0.9000    1.0000

  With constraints ：

Output Arguments

collapse all

x — Regularly-spaced vector
row vector

Regularly-spaced vector, returned as a row vector. If j > k, then x = j:k is an empty matrix. More generally, the syntax x = j:i:k returns an empty matrix when:

• i, j, or k is an empty input

• i == 0

• i > 0 and j > k

• i < 0 and j < k

 1.3 A(:,n), A(m,:), A(:), and A(j:k)  common indexing expressions General label expressions for arrays

A(:,n), A(m,:), A(:), and A(j:k) are common indexing expressions for a matrix A that contain a colon. When you use a colon as a subscript in an indexing expression, such as A(:,n), it acts as shorthand to include all subscripts in a particular array dimension. It is also common to create a vector with a colon for the purposes of indexing, such as A(j:k). Some indexing expressions combine both uses of the colon, as in A(:,j:k).

General label expression , A colon is a bit like a wildcard ：

Master as one 3by3 Matrix , 

A = magic(3)
A = 3×3

     8     1     6
     3     5     7
     4     9     2

• A(:,n) is the nth column of matrix A.【 The first n Column all elements 】

A(1,:)
ans = 1×3

     8     1     6

>> A(2,:)

ans =

     3     5     7

• A(m,:) is the mth row of matrix A.-【 The first m All elements of the row 】

>> A(:,1)

ans =

     8
     3
     4

>> A(:,2)

ans =

     1
     5
     9

• A(:,:,p) is the pth page of three-dimensional array A.【 One page The data of 】

>>  B = randn(4,3,2)

B(:,:,1) =

   -0.1924   -1.4224    1.4193
    0.8886    0.4882    0.2916
   -0.7648   -0.1774    0.1978
   -1.4023   -0.1961    1.5877

• A(:) reshapes all elements of A into a single column vector. This has no effect if A is already a column vector.【 Merge the columns of a two-dimensional array into 1 Column , Dimensionality has been reduced 】

>> A(:)

ans =

     8
     3
     4
     1
     5
     9
     6
     7
     2

Be careful ,3 The operation of dimension array cannot be done . 

• A(:,:) reshapes all elements of A into a two-dimensional matrix. This has no effect if A is already a matrix or vector. 【 Make the one-dimensional one again 2 It's not easy 】

>> A(:,:)

ans =

     8     1     6
     3     5     7
     4     9     2

• A(j:k) uses the vector j:k to index into A and is therefore equivalent to the vector [A(j), A(j+1), ..., A(k)].

From left to right , The order from top to bottom , take A From element j To the elements k, extracted , And compose a vector .

>> A(2:3)

ans =

     3     4

>> A(1:3)

ans =

     8     3     4

• A(:,j:k) includes all subscripts in the first dimension but uses the vector j:k to index in the second dimension. This returns a matrix with columns [A(:,j), A(:,j+1), ..., A(:,k)].

This means combination ： Here the parameter of the coordinate is the first dimension of the vector , The parameter on the right is the second dimension of the vector ：

So if A=

>> A(:,:)

ans =

     8     1     6
     3     5     7
     4     9     2

that , 1 To 2 The column selection is

>> A(:,1:2)

ans =

     8     1
     3     5
     4     9

1 To 3 The column selection is ：

>> A(:,1:3)

ans =

     8     1     6
     3     5     7
     4     9     2

---

3 Examples and analysis ：

  Construct a 4 The magic square of the order ：

>> A = magic(4)

A =

    16     2     3    13
     5    11    10     8
     9     7     6    12
     4    14    15     1

Construct another 8 The magic square of the order ：

>> B = magic(8)

B =

    64     2     3    61    60     6     7    57
     9    55    54    12    13    51    50    16
    17    47    46    20    21    43    42    24
    40    26    27    37    36    30    31    33
    32    34    35    29    28    38    39    25
    41    23    22    44    45    19    18    48
    49    15    14    52    53    11    10    56
     8    58    59     5     4    62    63     1

3.1 Extract data from a specified row in a specified order ：

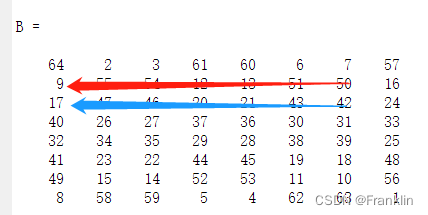
【 example 1】 From magic square B, Of the 2,3 That's ok , From 7 Column to the first 1 Column , In reverse or subtractive order （-1） Extract data

>> B(2:3,7:-1:1)

ans =

    50    51    13    12    54    55     9
    42    43    21    20    46    47    17

【 case , The characterization is as follows 】

【 Example 2 】 magic square A, From 3 To 4 That's ok ,2 To 4 Column , Extract data in positive order , The default is 1, therefore , Don't write ,

>> A(3:4,2:4)

ans =

     7     6    12
    14    15     1

 

 【 example 3】 Reference the last column of elements

>> A(:,end)

ans =

    13
     8
    12
     1

 【 Example 4 】 Reference to para 3 That's ok , Derivative number 2 Data

>> B(3,end - 1)

ans =

    42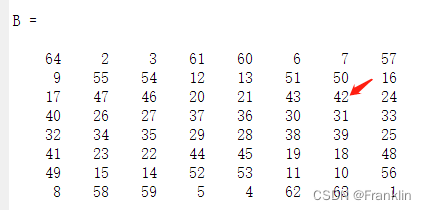

 

3.2 Complex data reorganization ：

Continue to use , The magic square matrix generated in the previous summary is used as an example ：

Example 5 , Extract uncertain rows and columns , Can be repeated , And reorganize them .

This case , take B Of the 1,3 Yes , The first 2,3 The columns are organized , Be careful , The first 3 That's ok , And the 2 Column , The first 3 The columns are all taken 2 Time

>> B([1 3 3],[2 2 3 3])

ans =

     2     2     3     3
    47    47    46    46
    47    47    46    46

 3.3 Wildcard examples of colons ：

example 6, We use it ： Do wildcard , Will a 3x3 The matrix of is extended to 3x3x3x2 Four dimensional matrix of

>>  C(:,:,1,2)=[1 2 3;4 5 6;7 8 9]

C(:,:,1,1) =

     0     0     0
     0     0     0
     0     0     0


C(:,:,1,2) =

     1     2     3
     4     5     6
     7     8     9

 【 case , The wildcard here occupies the 1,2 Vector dimension , We only give one 3x3 Matrix , Other matrices are automatically assigned to 0, Here we define the dimension 3by1& dimension 4by2 A value of , The system will automatically 3by1 The value of is 0】

>> C(:,:,2,2)=[9 8 1;6 5 4;3 2 1]

C(:,:,1,1) =

     0     0     0
     0     0     0
     0     0     0


C(:,:,2,1) =

     0     0     0
     0     0     0
     0     0     0


C(:,:,1,2) =

     1     2     3
     4     5     6
     7     8     9


C(:,:,2,2) =

     9     8     1
     6     5     4
     3     2     1

 【 case , We continue to assign dimensions 3by2& dimension 4by2 Value , The system automatically assigns other values 】

>> C(:,:,3,2)=[5 5 5;5 5 5;5 5 5]

C(:,:,1,1) =

     0     0     0
     0     0     0
     0     0     0


C(:,:,2,1) =

     0     0     0
     0     0     0
     0     0     0


C(:,:,3,1) =

     0     0     0
     0     0     0
     0     0     0


C(:,:,1,2) =

     1     2     3
     4     5     6
     7     8     9


C(:,:,2,2) =

     9     8     1
     6     5     4
     3     2     1


C(:,:,3,2) =

     5     5     5
     5     5     5
     5     5     5

 【 Empathy , The whole matrix is constructed 】

---

2 Reference to relevant names ：

2.1 unit-spaced vector 【 Unit interval vector  】

Pay attention to this and Unit vect Not quite the same. , Is the unit interval vector .

---

Reference resources ：

Vector creation, array subscripting, and for-loop iteration - MATLAB colon : (mathworks.com)

matlab Summary of common array operations _ The wind chaser YL The blog of -CSDN Blog _matlab Array