这篇笔记依然属于TD算法的范畴。Multi-Step-TD-Target 是对 TD算法的改进。
9. Multi-Step-TD-Target
9.1 Review Sarsa & Q-Learning
- Sarsa
- 训练 动作价值函数 \(Q_\pi(s,a)\);
- TD Target 是 \(y_t = r_t + \gamma\cdot Q_\pi(s_{t+1},a_{t+1})\)
- Q-Learning
- 训练 最优动作价值函数 Q-star;
- TD Target 是 \(y_t = r_t +\gamma \cdot \mathop{max}\limits_{a} Q^*({s_{t+1}},a)\)
- 注意,两种算法的 TD Target 的 r 部分 都只有一个奖励 \(r_t\)
- 如果用多个奖励,那么 RL 的效果会更好;Multi-Step-TD-Target就是基于这种考虑提出的。
在第一篇强化学习的基础概念篇中,就提到过,agent 会观测到以下这个轨迹:
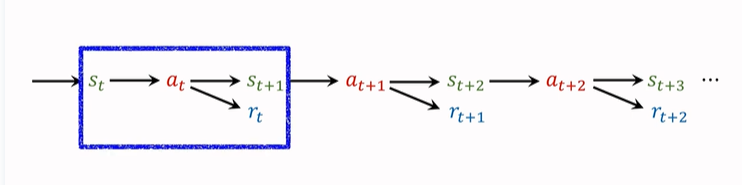
我们之前只使用一个 transition 来记录动作、奖励,并且更新 TD-Target。一个 transition 包括\((s_t,a_t,s_{t+1},r_t)\),只有一个奖励\(r_t\)。(如上图蓝框所示)。
这样算出来的 TD Target 就是 One Step TD Target。
其实我们也可以一次使用多个 transition 中的奖励,得到的 TD Target 就是 Multi-Step-TD-Target。如下图蓝框选择了两个 transition,同理接下来可以选后两个 transition 。
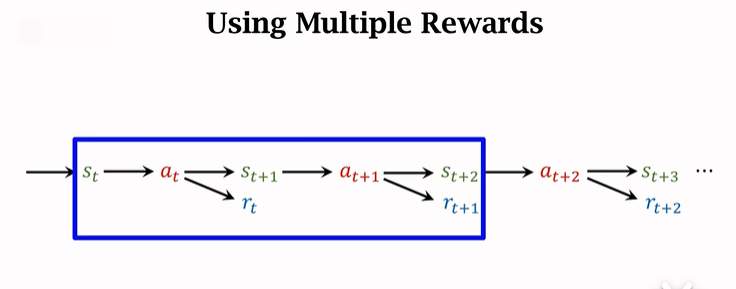
9.2 多步折扣回报
Multi-Step Return.
折扣回报公式为:\(U_t=R_t+\gamma\cdot{U_{t+1}}\);
这个式子建立了 t 时刻和 t+1 时刻的 U 的关系,为了得到多步折扣回报,我们递归使用这个式子:
\(U_t=R_t+\gamma\cdot{U_{t+1}}\\=R_t+\gamma\cdot(R_{t+1}+\gamma\cdot{U_{t+2}})\\=R_t+\gamma\cdot{R_{t+1}}+\gamma^2\cdot{U_{t+2}}\)
这样,我们就可以包含两个奖励,同理我们可以有三个奖励......递归下去,包含 m个奖励为:
\(U_t=\sum_{i=0}^{m-1}\gamma^i\cdot{R_{t+i}}+\gamma^m\cdot{U_{t+m}}\)
即:回报 \(U_t\) 等于 m 个奖励的加权和,再加上 \(\gamma^m\cdot{U_{t+m}}\),后面这一项称为 多步回报。
现在我们推出了 多步的 \(U_t\) 的公式,进一步可以推出 多步 \(y_t\) 的公式,即分别对等式两侧求期望,使随机变量具体化:
Sarsa 的 m-step TD target:
\(y_t=∑_{i=0}^{m−1}\gamma^i\cdot r_{t+i}+\gamma^m\cdot{Q_\pi}(s_{t+m},a_{t+m})\)
注意:m=1 时,就是之前我们熟知的标准 TD Target。
多步的 TD Target 效果要比 单步 好。
Q-Learning 的 m-step TD target:
\(y_t = \sum_{i=0}^{m-1}\gamma^i{r_{t+i}}+\gamma^m\cdot\mathop{max}\limits_{a} Q^*({s_{t+m}},a)\)
同样,m=1时,就是之前的TD Target。
9.3 单步 与 多步 的对比
单步 TD Target 中,只使用一个奖励 \(r_t\);
如果用多步TD Target,则会使用多个奖励:\(r_t,r_{t+1},...,r_{t+m-1}\)
联想一下第二篇 价值学习 的旅途的例子,如果真实走过的路程占比越高,不考虑 “成本” 的情况下,对于旅程花费时间的估计可靠性会更高。
m 是一个超参数,需要手动调整,如果调的合适,效果会好很多。


![Jerry's test box configuration channel [chapter]](/img/d4/fb67f5ee0fe413c22e4e5cd5037938.png)