当前位置:网站首页>【矩阵乘】【NOI 2012】【cogs963】随机数生成器
【矩阵乘】【NOI 2012】【cogs963】随机数生成器
2022-07-07 20:03:00 【全栈程序员站长】
大家好,又见面了,我是全栈君。
963. [NOI2012] 随机数生成器
** 输入文件:randoma.in 输出文件:randoma.out 简单对照
时间限制:1 s 内存限制:128 MB**【问题描写叙述】
栋栋近期迷上了随机算法,而随机数是生成随机算法的基础。栋栋准备使用线性同余法(Linear Congruential Method)来生成一个随机数列。这样的方法须要设置四个非负整数參数m,a,c,X[0],依照以下的公式生成出一系列随机数{Xn}:
X[n+1]=(aX[n]+c) mod m当中mod m表示前面的数除以m的余数。从这个式子能够看出,这个序列的下一个数总是由上一个数生成的。
用这样的方法生成的序列具有随机序列的性质。因此这样的方法被广泛地使用,包括经常使用的C++和Pascal的产生随机数的库函数使用的也是这样的方法。
栋栋知道这样产生的序列具有良好的随机性,只是心急的他仍然想尽快知道X[n]是多少。
由于栋栋须要的随机数是0,1,…,g-1之间的,他须要将X[n]除以g取余得到他想要的数,即X[n] mod g,你仅仅须要告诉栋栋他想要的数X[n] mod g是多少就能够了。
【输入格式】
输入文件randoma.in中包括6个用空格切割的整数m,a,c,X[0],n和g,当中a,c,X[0]是非负整数。m,n,g是正整数。
【输出格式】
输出到文件randoma.out中,输出一个数,即X[n] mod g
【例子输入】
11 8 7 1 5 3【例子输出】
2【例子说明】
计算得X[n]=X[5]=8,故(X[n] mod g) = (8 mod 3) = 2【数据规模】
40%的数据中m为质数
30%的数据中m与a-1互质
50%的数据中n<=10^6
100%的数据中n<=10^18
40%的数据m,a,c,X[0]<=10^4
85%的数据m,a,c,X[0]<=10^9
100%的数据中m,a,c,X[0]<=10^18
100%的数据中g<=10^8
对于全部数据,n>=1,m>=1,a>=0,c>=0,X[0]>=0,g>=1。题解:
比較简单的矩阵乘,对于两个矩阵:
A[a,c0,1]
B[X[n−1]1]
显然,X[n]能够由这两个矩阵相乘得到: A∗B=C[X[n]1]
于是对于X[n],我们能够这样求: An∗[X[0]1]
比較坑人的是须要写高速乘,由于普通乘会炸。。。 (PS:高速乘差点儿和高速幂写起来一样,仅仅须要把 * 改成 +)
Code:
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
long long A[2][2]={{0,0},{0,1}},B[2][2]={{0,0},{1,0}},C[2][2]={0};
long long n,g,m,nn;
long long kc(long long x,long long y){
long long z=0;
x%=m; y%=m;
if (x<y) swap(x,y);
while (y){
if (y&1) z=(z+x)%m;
x=(2*x)%m;
y>>=1;
}
return z;
}
int main(){
scanf("%lld%lld%lld%lld%lld%lld",&m,&A[0][0],&A[0][1],&B[0][0],&n,&g);
nn=n;
while (nn){
if (nn&1){
memset(C,0,sizeof(C));
for (int i=0; i<2; i++)
for (int j=0; j<2; j++)
for (int k=0; k<2; k++)
C[i][j]=(C[i][j]+kc(A[i][k],B[k][j]))%m;
for (int i=0; i<2; i++)
for (int j=0; j<2; j++)
B[i][j]=C[i][j];
}
nn>>=1;
memset(C,0,sizeof(C));
for (int i=0; i<2; i++)
for (int j=0; j<2; j++)
for (int k=0; k<2; k++)
C[i][j]=(C[i][j]+kc(A[i][k],A[k][j]))%m;
for (int i=0; i<2; i++)
for (int j=0; j<2; j++)
A[i][j]=C[i][j];
}
printf("%lld\n",B[0][0]%g);
return 0;
}发布者:全栈程序员栈长,转载请注明出处:https://javaforall.cn/116386.html原文链接:https://javaforall.cn
边栏推荐
- 理财产品要怎么选?新手还什么都不懂
- Details of C language integer and floating-point data storage in memory (including details of original code, inverse code, complement, size end storage, etc.)
- How to choose fund products? What fund is suitable to buy in July 2022?
- 写一下跳表
- Referrer和Referrer-Policy简介
- 九度 1201 -二叉排序数遍历- 二叉排序树「建议收藏」
- 【函数递归】简单递归的5个经典例子,你都会吗?
- DataTable数据转换为实体
- When easygbs cascades, how to solve the streaming failure and screen jam caused by the restart of the superior platform?
- Helix QAC 2020.2新版静态测试工具,最大限度扩展了标准合规性的覆盖范围
猜你喜欢

如何满足医疗设备对安全性和保密性的双重需求?
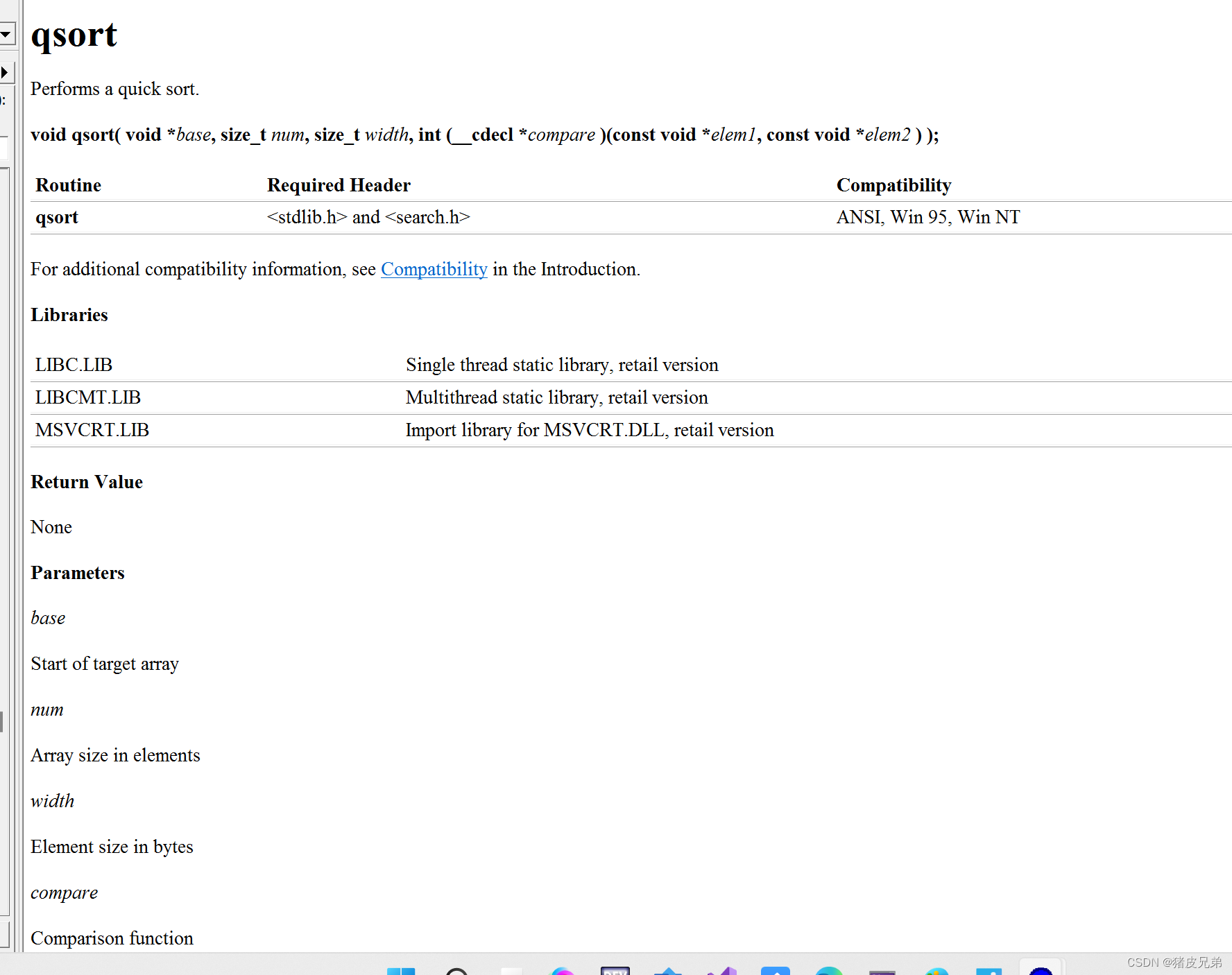
C language helps you understand pointers from multiple perspectives (1. Character pointers 2. Array pointers and pointer arrays, array parameter passing and pointer parameter passing 3. Function point
【C语言】指针进阶---指针你真的学懂了吗?

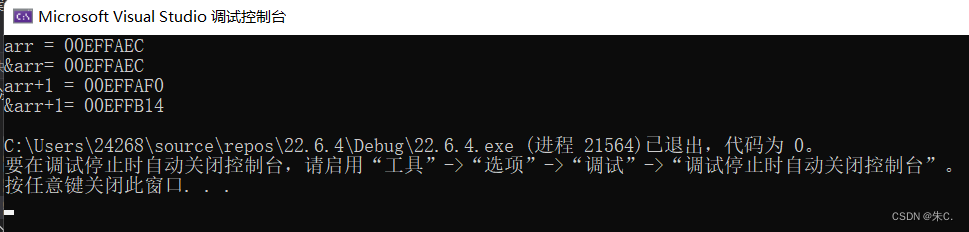
Static analysis of software defects codesonar 5.2 release

CodeSonar如何帮助无人机查找软件缺陷?

ERROR: 1064 (42000): You have an error in your SQL syntax; check the manual that corresponds to your
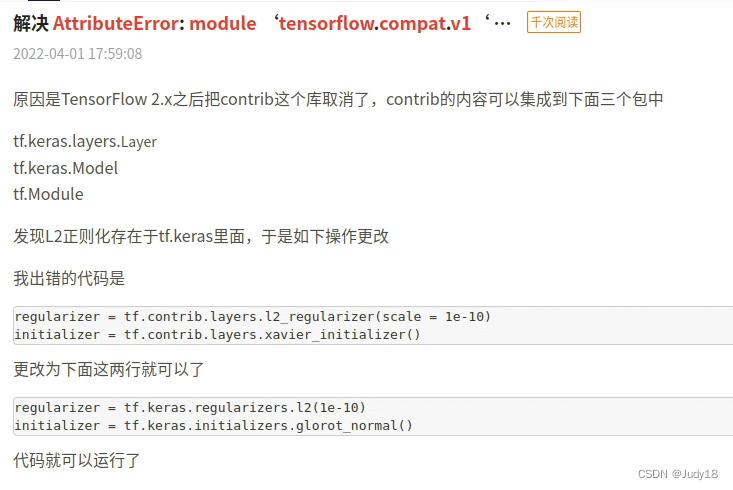
Tensorflow2.x下如何运行1.x的代码

Implement secondary index with Gaussian redis
Codesonar enhances software reliability through innovative static analysis

95年专注安全这一件事 沃尔沃未来聚焦智能驾驶与电气化领域安全
随机推荐
Lingyun going to sea | yidiantianxia & Huawei cloud: promoting the globalization of Chinese e-commerce enterprise brands
静态测试工具
You want to kill a port process, but you can't find it in the service list. You can find this process and kill it through the command line to reduce restarting the computer and find the root cause of
Don't fall behind! Simple and easy-to-use low code development to quickly build an intelligent management information system
[function recursion] do you know all five classic examples of simple recursion?
部署、收回和删除解决方式—-STSADM和PowerShell「建议收藏」
JNI 初级接触
easyui 日期控件清空值
Nebula importer data import practice
Numerical method for solving optimal control problem (0) -- Definition
备份 TiDB 集群到持久卷
万字总结数据存储,三大知识点
95年专注安全这一件事 沃尔沃未来聚焦智能驾驶与电气化领域安全
Codesonar enhances software reliability through innovative static analysis
I Basic concepts
Intelligent software analysis platform embold
[concept of network principle]
如何满足医疗设备对安全性和保密性的双重需求?
Onespin | solve the problems of hardware Trojan horse and security trust in IC Design
margin 等高布局