当前位置:网站首页>万字总结数据存储,三大知识点
万字总结数据存储,三大知识点
2022-07-07 18:25:00 【猪皮兄弟】
🧸🧸🧸各位巨佬大家好,我是猪皮兄弟🧸🧸🧸
这里是下面要讲的知识内容🥳🥳🥳
前言
今天我们学习的内容是数据的存储(包括大小端字节序)下面的内容非常之硬核,拿上小板凳,今天的内容正式开始!!!!
一、数据存储存在的意义
1.使用这个类型开辟内存空间的大小(大小决定了使用范围)
2.类型决定如何看待内存空间的视角
二、类型的基本归类
1.整型家族
整型家族:(虽然char是字符类型,但是字符类型存储的时候,存储的是字符的ASCLL码值,ASCLL码值是整数,所以归类到整型家族),下面附上一张图来叙述

总的来说,就是有符号和无符号的概念
2.浮点型家族
浮点型家族:
float,double,long double
3.构造类型
构造类型 (自定义类型,自己去创造)
·数组类型
·结构体类型 struct
·枚举类型 enum
·联合类型 union
4.指针类型
5.空类型
空类型(也就是void类型,也叫无类型)
void test(void)//不需要parameter时,可以写成void,也可以不写
有一种指针是void*类型的指针
三、整型提升与算术转换(下面的计算会用到)!!!
1.隐式类型转换
概念:
C的整型算术运算总是至少以缺省整型类型的精度来进行的。
为了获得这个精度,表达式中的字符和短整型操作数在使用前被转换为普通整型,这种转换称为整型提升。
2.整型提升的意义
表达式的整型运算要在CPU的相应运算器件内执行,CPU内整型运算器ALU的操作数的字节长度一般就是int的字节长度,同时也是CPU的通用寄存器的长度。
因此,即使两个char类型的相加,在CPU执行时实际上也要先转换为CPU内整型操作数的标准长度。(也就是int)
表达式中各种长度可能小于int长度的整型值,都必须转换为int 或unsigned int,然后才能送入CPU去执行运算
3.整型提升的相关计算
无符号数也就是unsigned类型的数,它与有符号数signed类型相比,最高位就不是符号位了,也用来算数据大小
比如
在整型提升的时候,如果最高位是1则补1,如果最高位是0,则补0;
小于整型的都转换为int 或unsigned int
然后再参与运算
例1
char a=-1;
10000000 00000000 00000000 00000001//-1的原码
11111111 11111111 111111111 11111111//-1的补码
11111111 int类型—>char类型(发生截断)
printf(“%d”,a);,因为%d是打印有符号整型的,所以需要int类型,char类型只有一个字节的大小,不够,所以发生整型提升
11111111 11111111 11111111 11111111发生整形提升
char a=-1;
10000000 00000000 00000000 00000001//-1的原码
11111111 11111111 111111111 11111111//-1的补码
11111111 int类型—>char类型(发生截断)
printf(“%d”,a);,因为%d是打印有符号整型的,所以需要int类型,char类型只有一个字节的大小,不够,所以发生整型提升
11111111 11111111 11111111 11111111发生整形提升
例二
char a=5
存的是00000101(第一位当符号位看)
char b=126
存的是01111110(第一位当符号位看)
char c=a+b;
00000101
01111110
在加的时候达不到一个整型,会发生整形提升
00000000 00000000 00000000 00000101-a
00000000 00000000 00000000 011111110-b
00000000 00000000 00000000 10000011
再截断
10000011-c
11111111 11111111 1111111 10000011
1000000 0000000 0000000 01111101-c的原码(符号位不变,其他位按位取反)
所以得到-125
4.算术转换
算术转换也就是字节小的数据类型向字节大的数据类型发生转换
四、整型在内存中的存储
首先呢,数据在计算机中的存储都是二进制的,不同的类型只是存的方式有所不同。
计算机中整型有三种表示方法:原码、反码、补码
注意了,是整型,浮点型是不说原反补码的
原码、反码、补码
①正负数原反补码的转换方法
整型在内存中存的是补码
三种表示方法都有符号位和数值位两部分
计算方法如下:
1.正数的原码反码补码都相同
2.负数额原码,反码,补码表示方式各不相同
负数的反码等于原码除符号位外其他位按位取反
再反码的基础上,再加1就得到了该负数的补码
3.负数的补码----->原码
可以先将负数的补码-1再除符号位外按位取反
也可以将负数的补码除符号位外按位取反再1
例图:
数据的表示形式
②数据为什么是以补码的形式存储
在计算机系统中,数值一律用补码来表示
原因在于:
使用补码,可以将符号位和数值域统一处理
同时,加法和减法也可以统一处理(CPU中只有加法器),此外补码与原码相互转换,其运算过程是相同的,不需要额外的硬件电路
这里有个例子可以说明CPU中没有减法器
例图:
而内存中如果存的是1000…后面一堆零
比如char 类型的 10000000 (补码),他没有可减的了,会直接被解析成-128,这是很重要的
③举几个例子
一、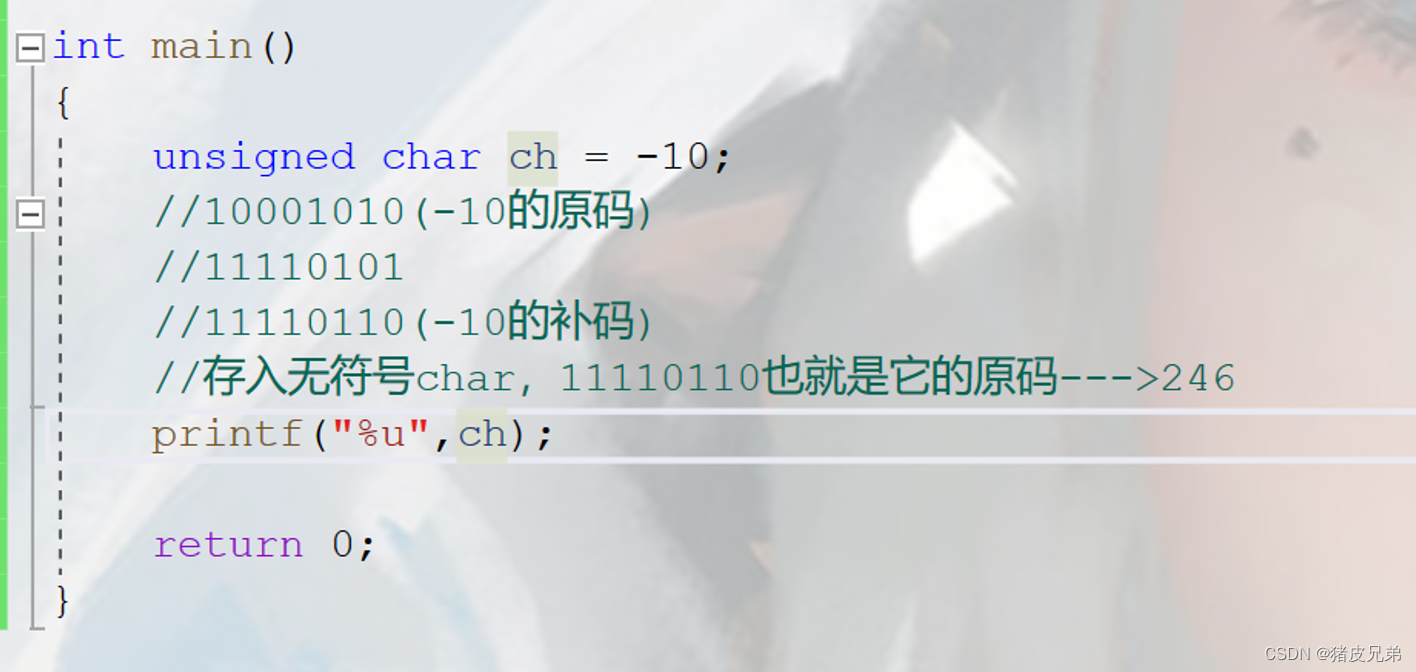
打印无符号数的值要用%u
%u是打印无符号数,意思是你要我打印的一定是无符号数,不是无符号数我也认为是无符号数
%d是打印有符号数的,意思是你要我打印的一定是有符号数,不是有符号数我也认为是有符号数
但是unsigned int ch=-10;
就已经把ch赋值成正数了(因为ch的类型是unsigned char);所以下面用%d和%u打印都没关系
但是下面这样就不行了
再比如:(整型提升在上面讲到过)
int main()
{
char a = -128;
//-128补码11111111 11111111 11111111 10000000
//存到a中发生截断 10000000
//要发生整型提升/因为高位是1,所以补1
//11111111 11111111 11111111 10000000
printf("%u",a);
return 0;
}
int main()
//{
int i = -20;
10000000 00000000 00000000 00010100
11111111 11111111 11111111 11101011
11111111 11111111 11111111 11101100
unsigned int j = 10;
00000000 00000000 00000000 00001010
printf("%d\n",i+j);
11111111 11111111 11111111 11110110
10000000 00000000 00000000 00001010
//结果-10
return 0;
}

对于char类型的存储来说,知道了这个就可以做下面那个题了
//题目1
#include <string.h>
int main()
{
char a[1000];
int i;
for (i = 0; i < 1000; i++)
{
a[i] = -1 - i;
}
printf("%d",strlen(a));
//255(因为遇到0就结束了,所以少了一个,不是256)
return 0;
}
//题目2
unsigned char i = 0;
int main()
{
for (i = 0; i <= 255; i++)
{
//因为i的值会在0-255之间循环,所以结果是死循环
printf("hello world\n");
}
return 0;
}
到了这里,整数在计算机当中的存储就讲完了,喝口茶,接下来,我们继续研究浮点数在计算机当中的存储

五、浮点数在内存当中的存储
常见的浮点数:
3.14159
1E10//这是浮点数的科学计数法的表示形式,也就是1.0*10^10
浮点型家族包括 float,double ,long double
浮点数表示的范围是在float.h中定义的

1.整数和浮点数在内存当中的存储的差异
先看看下面的代码,你觉得它的值是什么呢
int main()
{
int n = 9;
float* pFloat = (float*)&n;//int*
printf("n的值为:%d\n",n);
printf("*pFloat的值为:%f\n", *pFloat);
*pFloat = 9.0;
printf("n的值为:%d\n", n);
printf("*pFloat的值为:%f\n", *pFloat);
return 0;
}
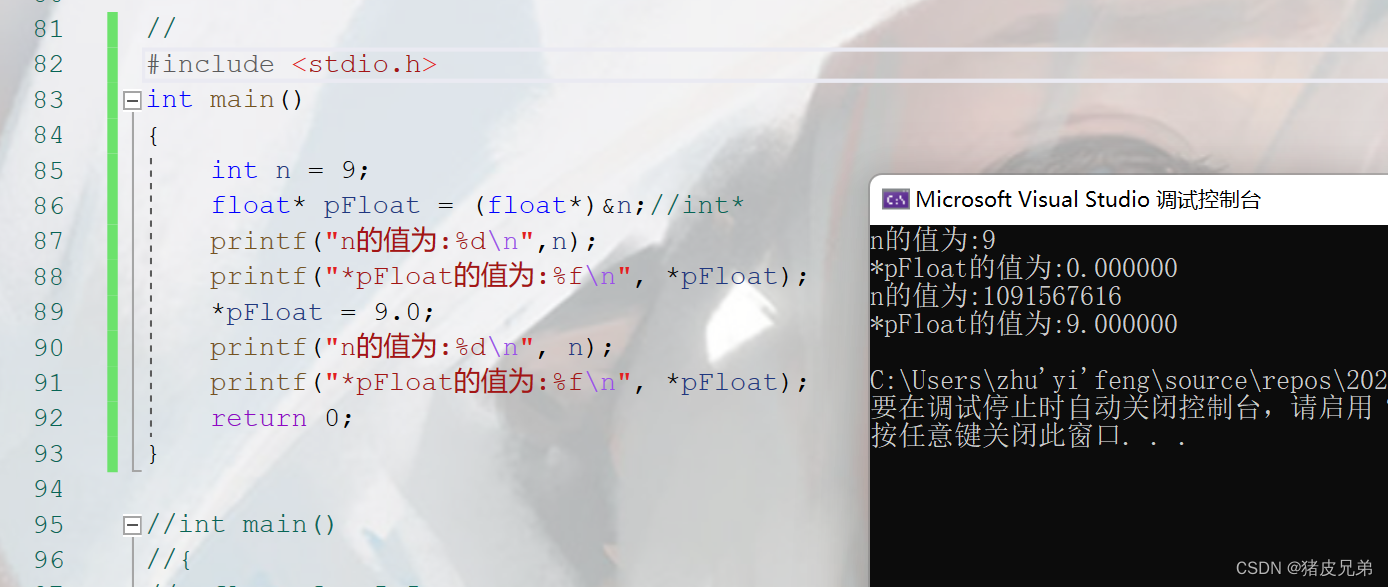
结果和你想的是不是一样的呢?
float a=5.5;
5.5的二进制并不是101.101,那么它该等于多少呢?
我们知道,二进制111每位分别表示的是
1x(2^1) 、1x(2^1) 、 1x(2^0)
那么,0.5就是1x(2^-1)
所以,5.5的二进制其实是101.1
用科学计数法来表示的话,就是1.001 * 2^2
再加上符号位的话就是(-1)^0 * 1.001 * 2^2
那么9.0该如何表示呢?
那3.14呢?
3.14的二进制存储其实是
11.00000…(后面有很多个0或1),目的是让他尽可能的接近3.14
所以,从这可以看出很多浮点数在计算机当中不能精确保存
所以,也不能用浮点数来做比较,只能是用浮点数来减去某一个值,判断结果是否在你规定的误差范围内
2.浮点数的存储
IEEE 754规定
SME
对于32位的浮点数,最高的1位是符号位S,接着的8位是指数E,剩下的23位为有效数字M
对于64位的浮点数,最高的1位是符号位S,接着的11位是指数E,剩下的52位为有效数字M
因为在计算机内部保存的时候,默认这个数的第一位总是1,因此可以被舍去,只保存后面的xxxxx部分。比如保存1.01时,只保存01,这样就可以节省一位空间,使精度更高
对于指数E
首先,E为一个无符号整数
这意味着,如果E为8位,那么范围是0-255,如果E为11位,那么范围是0-2047
但是,我们知道E是可以为负的,就像上面这个例子
所以IEEE 754又规定
存入内存时E的真实值必须再加上一个中间数,对于8位的E,这个中间数是127;对与11位是1023
也就是说存-1的时候先加上127或者1023,加正数的时候也是这样
目的是为了使负数变成正数
int main()
{
float f = 5.5;
101.1
(-1)^0*1.011*2^2
S=0;//S是符号位
E=2; 2+127=129 10000001// E所占的8个bit是无符号整型
M=1.011
存储到内存;
0 10000001 01100000000000000000000//M保存011,后面补0
化成十六进制
0100 0000 1011 0000 0000 0000 0000 0000
结果应该是0x40b00000
return 0;
}
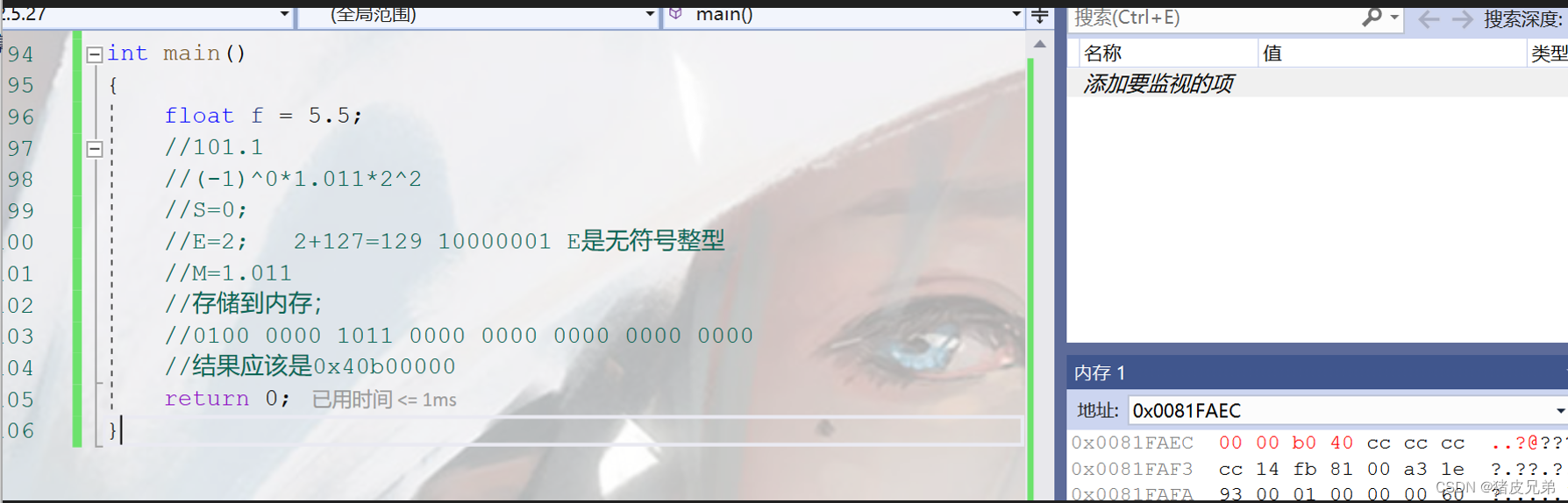
这里的地址呢就涉及到了大小端的问题,在下面会讲解
指数E从内存中取出来还可以分为三种情况
E不全为0或不全为1
那么就-127或-1023得到真实值(因为前面加了127或者1023)
E为全0
这时,1-127(或者1-1023)就是真实值
有效数字也不再加上前面的1,直接还原为0.xxxxxx的小数,这样做是为了表示±0,以便接近于0的很小的数字
E为全1
这时,如果有效数字M全为0,表示±∞(正负取决于符号位S)
int main()
{
int n = 9;
00000000 00000000 00000000 00001001
//浮点数认为是
0 00000000 00000000000000000001001
认为真实的
E是1-127 -> -126
M是0.00000000000000000001001
S是0
(-1)^0 * 0.00000000000000000001001 * 2(-126) ->0.000000
float* pFloat = (float*)&n;
printf("n的值为:%d\n",n);
printf("*pFloat的值为:%f\n", *pFloat);
*pFloat = 9.0;//1001.0
S=0,M=1.001, E=3 (3+127存进去)
0 10000010 00100000000000000000000
%f打印就是9.000000
用%d打印他又认为是很大的一个整数
printf("n的值为:%d\n", n);
printf("*pFloat的值为:%f\n", *pFloat);
return 0;
}
六、大小端字节序
1.大小端字节序存储的概念
数据的左边是高位,右边是低位
大小端字节序存储的概念
1.大端字节序存储:把一个数据低位字节处的数据存放在高地址,把高位字节处的数据存放在低地址处。
2.小端字节序存储:把一个数据低位字节处的数据存放在高地址,把高位字节处的数据存放在低地址处。
2.为什么会有大小端字节序
因为在计算机系统中,我们是以字节为单位的,每个地址单元都对应着一个字节。一个字节为8个bit,但是在C语言中,除了8bit的char外,还有16bit的short,32bit的long,int这些。
对于位数大于8bit的处理器,例如16位或32位的处理器,由于寄存器的宽度大于一个字节,那么必然存在着一个如何将多个字节安排的问题。因此就导致了大小端模式的出现
3.大小端字节序的简单判断
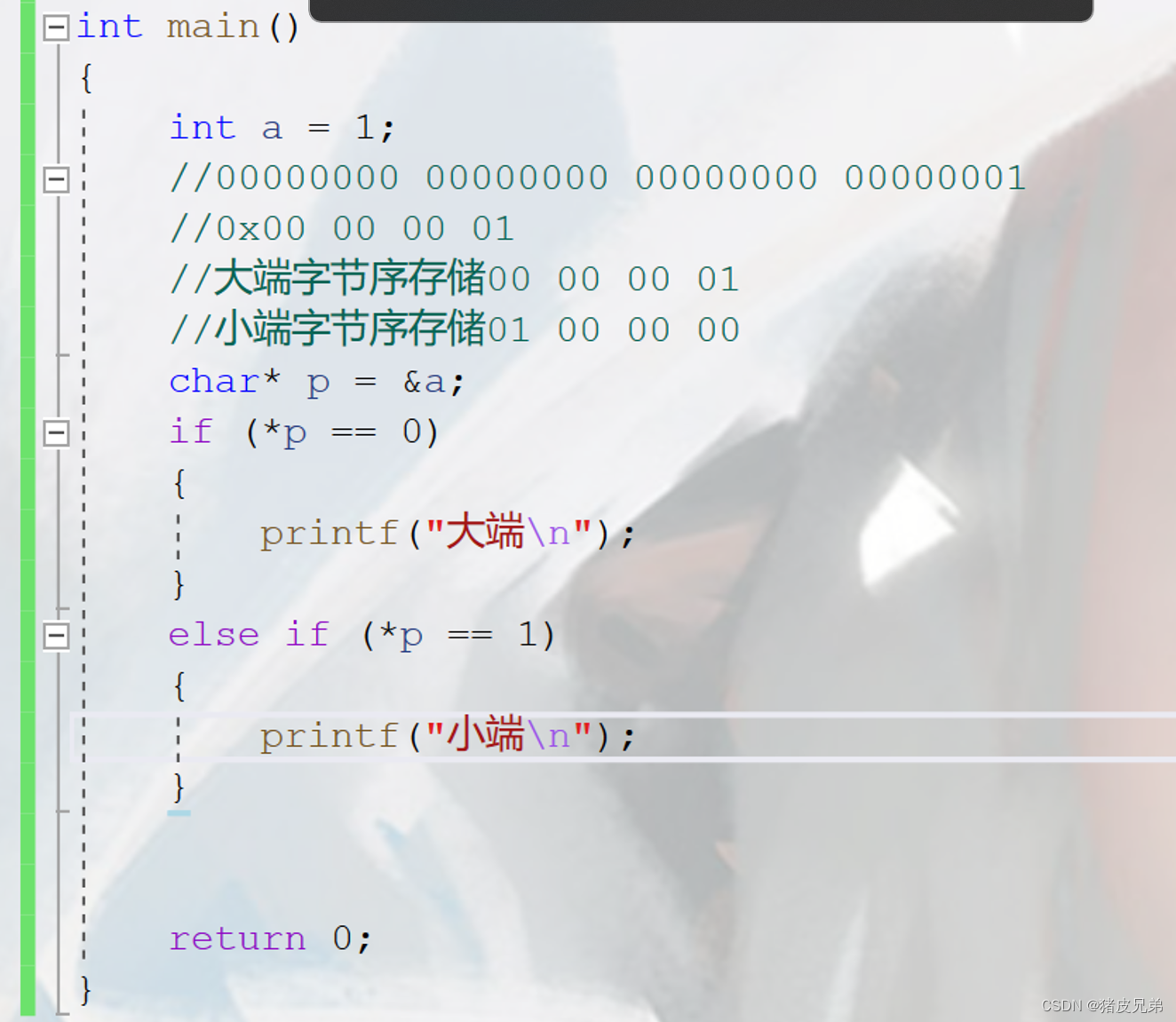
好了,今天的扫雷游戏就到这里,感谢大家对猪皮的支持!!!
七、五彩斑斓的一些废话
当你看到这里,相信上面的内容已经倒背如流了吧️️️。各位巨佬如果觉得有帮助的话,还望各位父老乡亲动动小手指点点点。一键三连有问题吗?没有问题,这都是什么?人情世故
边栏推荐
- 深度学习模型压缩与加速技术(七):混合方式
- AIRIOT助力城市管廊工程,智慧物联守护城市生命线
- Force buckle 1961 Check whether the string is an array prefix
- 《数字图像处理原理与实践(MATLAB版)》一书之代码Part2[通俗易懂]
- TS quick start - Generic
- php 获取图片信息的方法
- c语言如何判定是32位系统还是64位系统
- Creation of kubernetes mysql8
- Traversée des procédures stockées Oracle
- Force buckle 643 Subarray maximum average I
猜你喜欢
【mysql篇-基础篇】事务
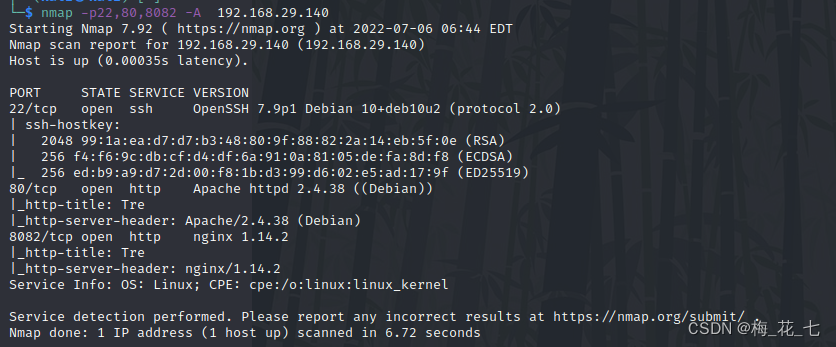
Vulnhub tre1

ERROR: 1064 (42000): You have an error in your SQL syntax; check the manual that corresponds to your

Measure the height of the building
不落人后!简单好用的低代码开发,快速搭建智慧管理信息系统
Apifox 接口一体化管理新神器

测量楼的高度

Dachang classic pointer written test questions
![[philosophy and practice] the way of program design](/img/c8/93f2ac7c5beb95f64b7883ad63c74c.jpg)
[philosophy and practice] the way of program design
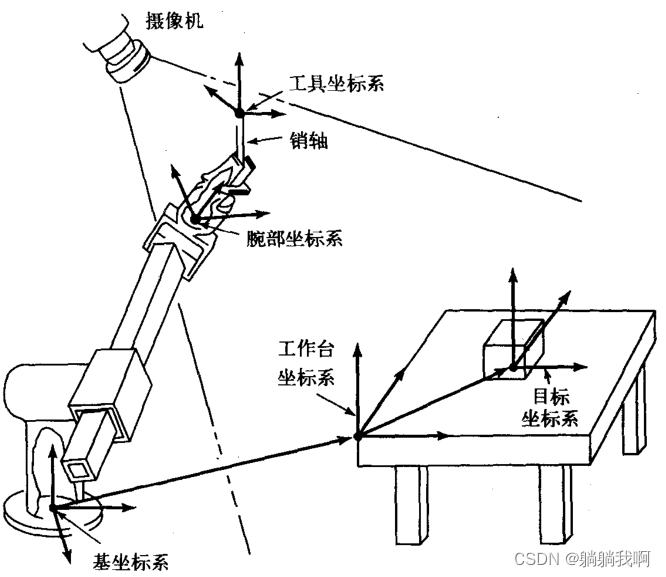
Small guide for rapid formation of manipulator (11): standard nomenclature of coordinate system
随机推荐
Force buckle 459 Duplicate substring
机械臂速成小指南(十二):逆运动学分析
Meta Force原力元宇宙系统开发佛萨奇模式
JNI 初级接触
图扑数字孪生煤矿开采系统,打造采煤“硬实力”
When easygbs cascades, how to solve the streaming failure and screen jam caused by the restart of the superior platform?
软件缺陷静态分析 CodeSonar 5.2 新版发布
Yolov6:yolov6+win10--- train your own dataset
Dachang classic pointer written test questions
Small guide for rapid formation of manipulator (12): inverse kinematics analysis
《数字图像处理原理与实践(MATLAB版)》一书之代码Part2[通俗易懂]
Force buckle 2315 Statistical asterisk
Graduation season | regretful and lucky graduation season
Force buckle 674 Longest continuous increasing sequence
Cantata9.0 | 全 新 功 能
开发那些事儿:Go加C.free释放内存,编译报错是什么原因?
取两个集合的交集
ISO 26262 - 基于需求测试以外的考虑因素
Machine learning notes - explore object detection datasets using streamlit
备份 TiDB 集群到持久卷




