当前位置:网站首页>Numerical method for solving optimal control problem (0) -- Definition
Numerical method for solving optimal control problem (0) -- Definition
2022-07-07 20:29:00 【Favorite dish of chicken】
Basic description
This article gives a complete description of the optimal control problem .
The optimal control problem can be briefly described as : For a controlled system , Under the constraint conditions , Seek the optimal control quantity to minimize the performance index .
The mathematical description is : Find control variables u ( t ) ∈ R m \boldsymbol{u}(t) \in \mathbb{R}^m u(t)∈Rm, Make the performance index
J = Φ ( x ( t 0 ) , t 0 , x ( t f ) , t f ) + ∫ t 0 t f L ( x ( t ) , u ( t ) , d ) d t J = \Phi (\mathbf{x}(t_0),t_0,\mathbf{x}(t_f),t_f) + \int_{t_0}^{t_f} L(\mathbf{x}(t),\mathbf{u}(t),d) \text{d}t J=Φ(x(t0),t0,x(tf),tf)+∫t0tfL(x(t),u(t),d)dt
Minimum .
The state variables and control variables satisfy the following constraints :
x ˙ ( t ) = f ( x ( t ) , u ( t ) , t ) t ∈ [ t 0 , t f ] , ϕ ( x ( t 0 ) , t 0 , x ( t f ) , t f ) = 0 , C ( x ( t ) , u ( t ) , t ) ≤ 0. \begin{matrix} &\boldsymbol{\dot x}(t) = \boldsymbol{f}(\boldsymbol{x}(t),\boldsymbol{u}(t),t) \quad t \in [t_0,t_f], \\ &\phi (\boldsymbol{x}(t_0),t_0,\boldsymbol{x}(t_f),t_f)=0, \\ &\mathbf{C}(\mathbf{x}(t),\mathbf{u}(t),t) \le 0. \end{matrix} x˙(t)=f(x(t),u(t),t)t∈[t0,tf],ϕ(x(t0),t0,x(tf),tf)=0,C(x(t),u(t),t)≤0.
In style , x ( t ) ∈ R n \boldsymbol{x}(t) \in \mathbb{R}^n x(t)∈Rn Is the state variable , u ( t ) ∈ R m \boldsymbol{u}(t) \in \mathbb{R}^m u(t)∈Rm Is the control variable , t 0 t_0 t0 Is the initial time , t f t_f tf Is the terminal time .
The boundary condition of the state variable satisfies :
x ∈ X ⊂ R n , X = { x ∈ R n : x l o w e r ≤ x ≤ x u p p e r } \boldsymbol{x} \in X \subset \mathbb{R}^n, \quad X = \left \{x \in \mathbb{R}^n: x_{lower} \le x \le x_{upper} \right \} x∈X⊂Rn,X={ x∈Rn:xlower≤x≤xupper}
x l o w e r x_{lower} xlower Is the lower bound of the state variable , x u p p e r x_{upper} xupper Is the upper bound of the state variable .
The boundary condition of the control variable satisfies :
u ∈ U ⊂ R m , U = { u ∈ R m : u l o w e r ≤ u ≤ u u p p e r } \boldsymbol{u} \in U \subset \mathbb{R}^m, \quad U = \left \{u \in \mathbb{R}^m: u_{lower} \le u \le u_{upper} \right \} u∈U⊂Rm,U={ u∈Rm:ulower≤u≤uupper}
u l o w e r u_{lower} ulower Is the lower bound of the control variable , u u p p e r u_{upper} uupper Is the upper bound of the control variable .
Upper form Φ , L , f , ϕ , C \mathit{\Phi}, L, \boldsymbol{f}, \phi, \boldsymbol{C} Φ,L,f,ϕ,C Defined as :
Φ : R n × R × R n × R → R , L : R n × R m × R → R , f : R n × R m × R → R n , ϕ : R n × R × R n × R → R q , f : R n × R m × R → R c , \begin{aligned} &\mathit{\Phi}: \ \mathbb{R}^n \times \mathbb{R} \times \mathbb{R}^n \times \mathbb{R} \rightarrow \mathbb{R}, \\ &L: \ \mathbb{R}^n \times \mathbb{R}^m \times \mathbb{R} \rightarrow \mathbb{R}, \\ &\boldsymbol{f}: \ \mathbb{R}^n \times \mathbb{R}^m \times \mathbb{R} \rightarrow \mathbb{R}^n, \\ &\phi: \ \mathbb{R}^n \times \mathbb{R} \times \mathbb{R}^n \times \mathbb{R} \rightarrow \mathbb{R}^q, \\ &\boldsymbol{f}: \ \mathbb{R}^n \times \mathbb{R}^m \times \mathbb{R} \rightarrow \mathbb{R}^c, \\ \end{aligned} Φ: Rn×R×Rn×R→R,L: Rn×Rm×R→R,f: Rn×Rm×R→Rn,ϕ: Rn×R×Rn×R→Rq,f: Rn×Rm×R→Rc,
Optimal control , The control quantity changes in time sequence , The solution result is several curves . After the control curve is determined , The state curve can be determined according to the differential dynamics system .
Part of the
The above optimal control problem generally consists of four parts , Respectively :
- Performance indicators ;
- Control system differential equation constraints ;
- Boundary constraints ;
- Path Constraint .
Performance indicators
The performance index is the objective function in the optimization problem , However, in the field of optimal control, we call it performance index . Performance index is an important symbol to measure the quality of control system , There are generally three forms , Namely :
- Mayer Type performance index ;
- Lagrange Type performance index ;
- Bolza Type performance index .
Mayer Type performance index
Also known as constant performance index , Only consider the state variables of the control system at the terminal time point 、 Control variables 、 Indicators of time and its composite relationship , Such as the time it takes for the aircraft to move to the specified position ( Terminal time ) etc. . The mathematical description is :
J = Φ ( x ( t 0 ) , t 0 , x ( t f ) , t f ) . J = \Phi (\mathbf{x}(t_0),t_0,\mathbf{x}(t_f),t_f). J=Φ(x(t0),t0,x(tf),tf).
Lagrange Type performance index
Also known as integral performance index , Only emphasize the requirements for the whole control process , This indicator includes the state variables in the whole time domain 、 Integral of control variables and their compound Relations , It can represent the energy consumption of the system , Such as the amount of heat consumption caused by the control process . The mathematical description is :
J = ∫ t 0 t f L ( x ( t ) , u ( t ) , d ) d t . J = \int_{t_0}^{t_f} L(\mathbf{x}(t),\mathbf{u}(t),d) \text{d}t. J=∫t0tfL(x(t),u(t),d)dt.
Bolza Type performance index
Also known as composite performance index , yes Mayer The type and Lagrange Type combination , It not only emphasizes the system state at the time of the terminal , It also emphasizes the requirements for the control system process . This form can be transformed into the above two forms under certain conditions , Therefore, when describing the performance index of general optimal control problems Bolza Type performance index . The mathematical description is :
J = Φ ( x ( t 0 ) , t 0 , x ( t f ) , t f ) + ∫ t 0 t f L ( x ( t ) , u ( t ) , d ) d t . J = \Phi (\mathbf{x}(t_0),t_0,\mathbf{x}(t_f),t_f) + \int_{t_0}^{t_f} L(\mathbf{x}(t),\mathbf{u}(t),d) \text{d}t. J=Φ(x(t0),t0,x(tf),tf)+∫t0tfL(x(t),u(t),d)dt.
Control system differential equation constraints
Optimization problems contain many constraints , The optimal control problem is also a special optimization problem , Its special feature is that the constraint conditions have differential equations .
Any control system needs to use differential equations to describe the motion process , For example, the aircraft is under the action of gravity and thrust , Combined with its own quality changes and other characteristics , Establish a dynamic differential equation that can describe its motion law ; The robot manipulator is subjected to torque , Combine your arm length 、 quality 、 Joint and other characteristics , Establish a dynamic differential equation that can describe its motion law . The above equations can be used as differential algebraic equations (Differential Algebraic Equation,DAE) describe , by :
x ˙ ( t ) = f ( x ( t ) , u ( t ) , t ) t ∈ [ t 0 , t f ] . \boldsymbol{\dot x}(t) = \boldsymbol{f}(\boldsymbol{x}(t),\boldsymbol{u}(t),t) \quad t \in [t_0,t_f]. x˙(t)=f(x(t),u(t),t)t∈[t0,tf].
Boundary constraints
It is often necessary to give the initial state or end state in the control system , Such as the height of the rocket when it was just launched 、 Speed, etc ( The initial state ), You need to specify the height of the rocket at the end 、 Speed, etc ( That is, the end state ). In the optimal control problem , The above state at a certain time point is called boundary constraint . The mathematical description is :
ϕ ( x ( t 0 ) , t 0 , x ( t f ) , t f ) = 0. \phi (\mathbf{x}(t_0),t_0,\mathbf{x}(t_f),t_f) = 0. ϕ(x(t0),t0,x(tf),tf)=0.
Path Constraint
The constraints that the control system must meet in the whole time period are called path constraints .
The difference between path constraints and boundary constraints is , Path constraints occur in the entire time period , Boundary constraints occur at a specific point in time .
Common path constraints include :
- The state variable is on the top of the whole control process 、 Lower limit , Such as aircraft location 、 Speed etc. ;
- The control variable is on the top of the whole control process 、 Lower limit , Such as the output power of the motor 、 Moment, etc ;
- On the function composed of state variables and control variables 、 Lower limit , For example, aircraft or robots need to ensure that they cannot pass through certain specific areas .
The mathematical description of path constraints is :
C ( x ( t ) , u ( t ) , t ) ≤ 0. \mathbf{C}(\mathbf{x}(t),\mathbf{u}(t),t) \le 0. C(x(t),u(t),t)≤0.
summary
thus , So as to give performance indicators 、 Control system differential equation constraints 、 Mathematical description of boundary constraints and path constraints . The above four parts completely define the optimal control problem .
Solve the optimal control problem , That is to solve the optimization problem that minimizes the performance index under the above three kinds of constraints .
边栏推荐
- Spark 判断DF为空
- Opencv learning notes high dynamic range (HDR) imaging
- Small guide for rapid formation of manipulator (12): inverse kinematics analysis
- kubernetes之创建mysql8
- 目标:不排斥 yaml 语法。争取快速上手
- 阿里云有奖体验:如何通过ECS挂载NAS文件系统
- 如何满足医疗设备对安全性和保密性的双重需求?
- 阿洛的烦恼
- Alibaba cloud award winning experience: how to mount NAS file system through ECS
- 微服务远程Debug,Nocalhost + Rainbond微服务开发第二弹
猜你喜欢

写了个 Markdown 命令行小工具,希望能提高园友们发文的效率!
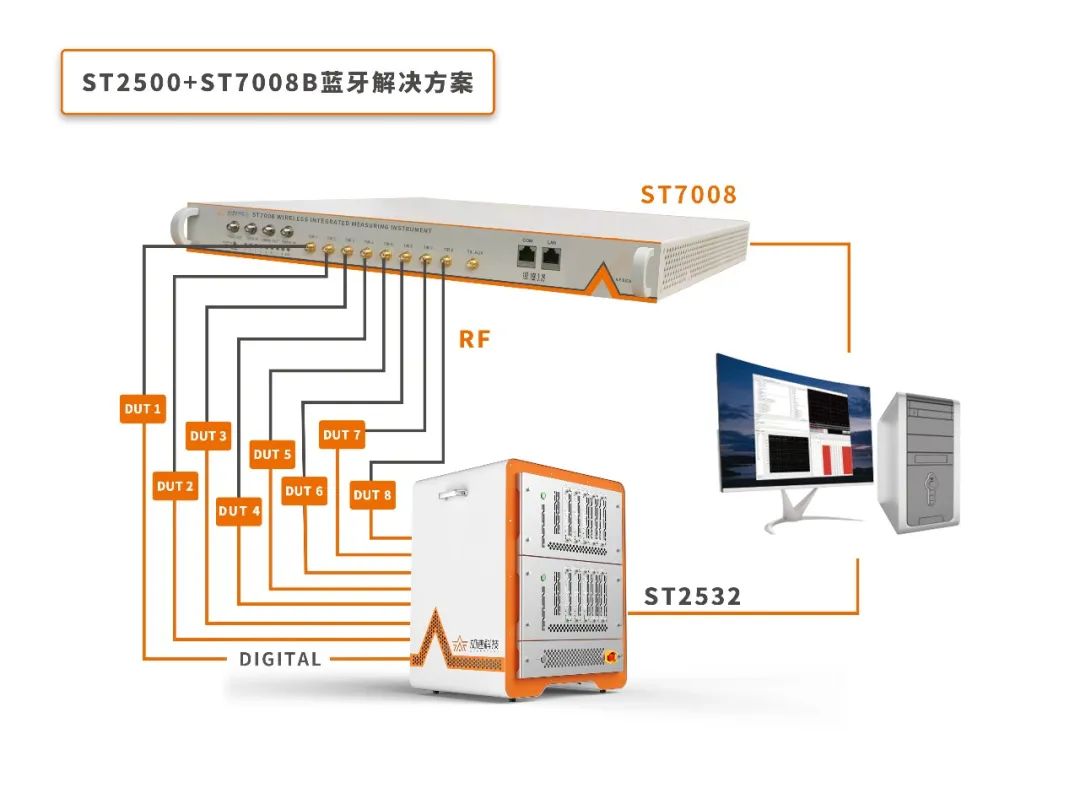
With st7008, the Bluetooth test is completely grasped

【论文阅读】MAPS: Multi-agent Reinforcement Learning-based Portfolio Management System
![嵌入式系统真正安全了吗?[ OneSpin如何为开发团队全面解决IC完整性问题 ]](/img/af/61b384b1b6ba46aa1a6011f8a30085.png)
嵌入式系统真正安全了吗?[ OneSpin如何为开发团队全面解决IC完整性问题 ]
让这个CRMEB单商户微信商城系统火起来,太好用了!

PHP method of obtaining image information
![[paper reading] maps: Multi-Agent Reinforcement Learning Based Portfolio Management System](/img/76/b725788272ba2dcdf866b28cbcc897.jpg)
[paper reading] maps: Multi-Agent Reinforcement Learning Based Portfolio Management System
不落人后!简单好用的低代码开发,快速搭建智慧管理信息系统

Airiot helps the urban pipe gallery project, and smart IOT guards the lifeline of the city
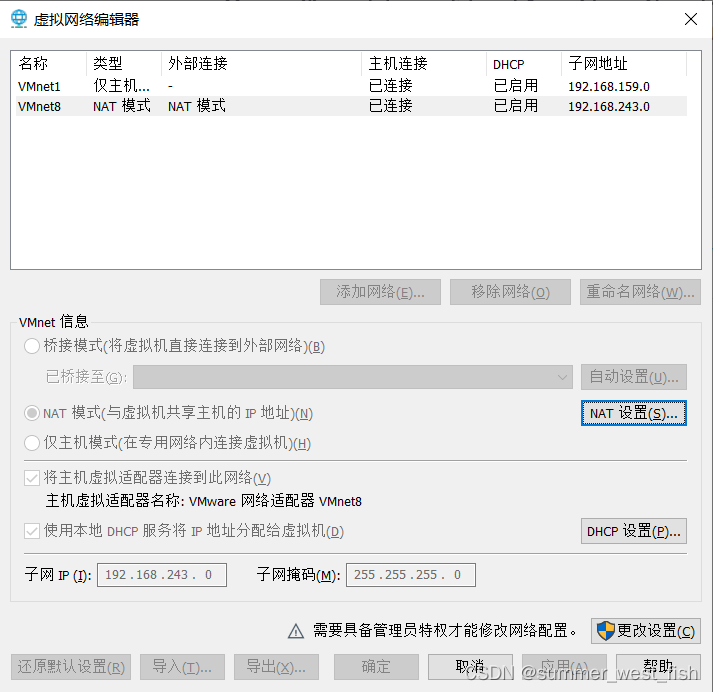
VMWare中虚拟机网络配置
随机推荐
AIRIOT助力城市管廊工程,智慧物联守护城市生命线
寫一下跳錶
Solve the problem of incomplete display around LCD display of rk3128 projector
[solution] package 'XXXX' is not in goroot
Small guide for rapid formation of manipulator (12): inverse kinematics analysis
【函数递归】简单递归的5个经典例子,你都会吗?
有用的win11小技巧
Validutil, "Rethinking the setting of semi supervised learning on graphs"
rk3128投影仪lcd显示四周显示不完整解决
ISO 26262 - 基于需求测试以外的考虑因素
一. 基础概念
目前股票开户安全吗?可以直接网上开户吗。
【OpenCV 例程200篇】223. 特征提取之多边形拟合(cv.approxPolyDP)
[philosophy and practice] the way of program design
凌云出海记 | 易点天下&华为云:推动中国电商企业品牌全球化
Tensorflow2.x下如何运行1.x的代码
Nebula Importer 数据导入实践
POJ 1742 coins (monotone queue solution) [suggestions collection]
Make this crmeb single merchant wechat mall system popular, so easy to use!
Implement secondary index with Gaussian redis