Details of C language integer and floating-point data storage in memory (including details of original code, inverse code, complement, size end storage, etc.)

For a deeper understanding of c Storage mode of internal data of language , First of all, we need to understand several commonly used types and their general classification . The preface first brings you some basic knowledge

Preface ：c Introduction to language data types

char // Character data type
short // Short
int // plastic
long // Long integer
long long // Longer plastic surgery
float // Single-precision floating-point
double // Double precision floating point

Careful observation shows that
It can be roughly divided into the following five categories
1、 Plastic surgery Family ：
Such as char、unsigned char、signed char、short、unsigned short [int]、signed short [int]、int、unsigned int、signed int、long、unsigned long [int]、signed long [int] etc.
2、 Floating point family ：
Such as float、double etc.
3、 Construction type ：
Such as array type 、 Type of structure struct、 Enumeration type enum、 Joint type union etc.
4、 Pointer types ：
Such as int pi、char pc、float pf、void pv etc.
5、 Empty type ：
void Indicates empty type （ No type ）
（ Usually applied to the return type of a function 、 The parameters of the function 、 Pointer types ）

With the above basic accumulation , Let's enter the text

1. Shaping storage in memory

The size of space is determined according to different types .
Such as int Type occupation 4 Bytes , So this 4 How are the bytes allocated ？
First of all, we need to understand the original code , Inverse code , Complement code

1.1 Original code 、 Inverse code 、 Some explanations of complement

    There are three ways to represent integers in a computer , The original code 、 Inverse and complement .
    The three representations have two parts: sign bit and numeric bit , The sign bits are all used 0 Express “ just ”, use 1 Express “ negative ”, The three representations of numeric bit negative integers are different .
 Original code 

Directly translate binary into binary in the form of positive and negative numbers .
Inverse code
Change the sign bit of the original code , The other bits can be inverted in turn .
Complement code
Inverse code +1 You get the complement .
*** notes ：*** A positive number 、 back 、 The complement is the same .
For plastic surgery ： Data stored in memory is actually stored in the complement .
（ Because in the computer system , All values are represented and stored by complements . The reason lies in , Use complement , Symbol bits and value fields can be treated in a unified way ; meanwhile , Addition and subtraction can also be handled in a unified way （CPU Only adders ） Besides , Complement code and original code are converted to each other , Its operation process is the same , No need for additional hardware circuits .）

1.2、 Large and small end storage mode

Let's look at the following simple code , Using the above knowledge, we first judge by ourselves 16 Base a Value , Check it again a How to store these numbers in memory
Decimal system a=20
Convert to binary 00000000000000000000000000010100
The positive integer original code is consistent with the inverse complement , Therefore, the complement stored in the computer memory is also
00000000000000000000000000010100
convert to 16 Base number （ Every four conversions ）
00 00 00 14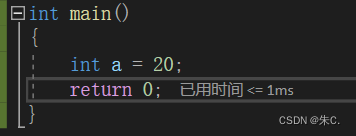

Let's now look at a stay vs How is it stored in the memory

Here we find vs The next storage is 14 00 00 00, It is in the opposite order of our calculation , Why is that ？
This is because there are some big end storage modes in different editors , Some are small end storage modes , Now let's introduce these two storage modes ：
What big end, small end ：
Big end （ Storage ） Pattern , The low bit of data is stored in the high address of memory , And the high end of the data , Stored in a low address in memory ;
The small end （ Storage ） Pattern , The low bit of data is stored in the low address of memory , And the high end of the data ,, Stored in a high address in memory .
Then we were just vs The memory information viewed in shows vs Next is the small end storage mode

Here we introduce a code question to judge whether the current editor is big end storage or small end storage

#include <stdio.h>
int check_sys()
{
    
 int i = 1;
 return (*(char *)&i);// hold i Cast the type to a byte and check i The content of the truncated address 
 // If it is 1, Small end storage mode , Anyway, it is the big end storage mode 
}
int main()
{
    
 int ret = check_sys();
 if(ret == 1)
 {
    
 printf(" The small end \n");
 }
 else
 {
    
 printf(" Big end \n");
 }
 return 0; }

This is a Baidu interview question , If you don't understand, please leave a message ！
Let me also give you a few simple codes to practice , The general rule is to write the original code, inverse code and complement of the data , Then it is judged by truncation or integer promotion , If you have not understand , Welcome to leave a message ！

1.
// What output ？
#include <stdio.h>
int main()
{
    
    char a= -1;
    signed char b=-1;
    unsigned char c=-1;
    printf("a=%d,b=%d,c=%d",a,b,c);
    return 0; }

2.
#include <stdio.h>
int main()
{
    
    char a = -128;
    printf("%u\n",a);
    return 0; }

3.
#include <stdio.h>
int main()
{
    
    char a = 128;
    printf("%u\n",a);
    return 0; }

4.
int i= -20;
unsigned  int  j = 10;
printf("%d\n", i+j); 
// Operate in the form of complement , Finally, it is formatted as a signed integer 

5.
unsigned int i;
for(i = 9; i >= 0; i--) {
    
    printf("%u\n",i);
}

6.
int main()
{
    
    char a[1000];
    int i;
    for(i=0; i<1000; i++)
   {
    
        a[i] = -1-i;
   }
    printf("%d",strlen(a));
    return 0; }

7.
#include <stdio.h>
unsigned char i = 0;
int main()
{
    
    for(i = 0;i<=255;i++)
   {
    
        printf("hello world\n");
   }
    return 0; }

The above is the storage of integer data in memory , Next, we discuss the storage of more complex floating-point numbers in memory

2、 Floating point storage in memory

According to international standards IEEE（ Institute of electrical and Electronic Engineering ） 754, Any binary floating point number V It can be expressed as form ：
(-1)^S * M * 2^E
(-1)^s The sign bit , When s=0,V Is a positive number ; When s=1,V It's a negative number .
M Represents a significant number , Greater than or equal to 1, Less than 2.
2^E Indicates the index bit .

for instance ：

Now we know how to convert floating-point numbers into international standards , that S M E How to store in memory ？ Now look at the picture ：
（1）32 Bit single precision floating point number

S Medium 0 perhaps 1 Stored in the first bit , The middle eight bits store E The numerical ,M The value of exists and the rest 23 In bits .
** however ！！！！** Pay attention to several stored points
**1、** because E Negative numbers may appear ,32 Storage under bit platform must +127 Then convert it into binary and store it ！
**2、** because M Before the decimal point, it will always be 1, So only the number after the decimal point is stored ！

（2）64 Bit double precision floating point number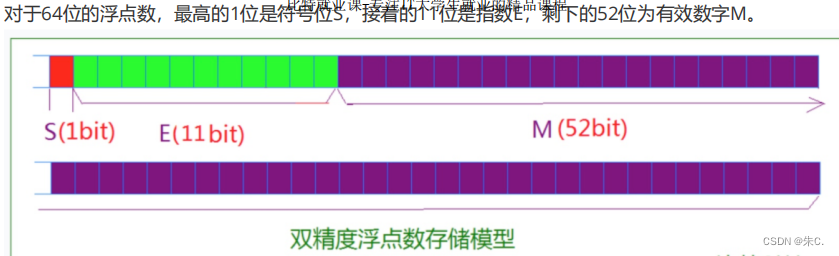

Here with 32 position Different Yes. E Plus 1023 Store it after

Let's talk about E Some special cases stored ：
1.E Not all for 0 Or not all of them 1
At this time , Floating point numbers are represented by the following rules , The index E The calculated value of minus 127（ or 1023）, Get the real value , then
Significant figures M Add the first 1.
such as ：
0.5（1/2） The binary form of is 0.1, Since it is stipulated that the positive part must be 1, That is to move the decimal point to the right 1 position , Then for 1.0*2^(-1), Its order code is -1+127=126, Expressed as 01111110, And the mantissa 1.0 Remove the integer part and make it 0, A filling 0 To 23 position 00000000000000000000000 , Then the second goes
The system is expressed as :
0 01111110 00000000000000000000000
2.E All for 0
At this time , The exponent of a floating point number E be equal to 1-127（ perhaps 1-1023） That's the true value ,
Significant figures M No more first 1, It's reduced to 0.xxxxxx Decimals of . This is to show that ±0, And close to
0 A very small number of .
3.E All for 1
At this time , If the significant number M All for 0, Express ± infinity （ It depends on the sign bit s）;

Finally, we use a topic to let you have a deeper understanding of the storage of floating-point numbers

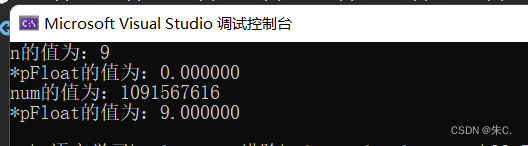
int main()
{
    
 int n = 9;
 float *pFloat = (float *)&n;
 printf("n The value of is ：%d\n",n);
 printf("*pFloat The value of is ：%f\n",*pFloat);
 *pFloat = 9.0;
 printf("num The value of is ：%d\n",n);
 printf("*pFloat The value of is ：%f\n",*pFloat);
 return 0; }

First ,9 -> 0000 0000 0000 0000 0000 0000 0000 1001
Because the index E All for 0, So the second case in the previous section . therefore , Floating point numbers V The just ：
V=(-1)^0 * 0.00000000000000000001001×2^{(-126)=1.001×2}(-146)
obviously ,V It's a very small one, close to 0 Positive number of , So the decimal number is 0.000000.
Let's look at the second part of the example .
Floating point number 9.0, How to express... In binary ？ How much is it to restore to decimal ？
First , Floating point numbers 9.0 Equal to binary 1001.0, namely 1.001×2^3.
9.0 -> 1001.0 ->(-1)^01.00123 -> s=0, M=1.001,E=3+127=130
that , The first sign bit s=0, Significant figures M be equal to 001 Add... To the back 20 individual 0, Cramming 23 position , Index E be equal to 3+127=130, namely 10000010.
therefore , Written in binary form , Should be s+E+M, namely
0 10000010 001 0000 0000 0000 0000 0000
This 32 The binary number of bits , Restore to decimal , It is 1091567616 .

The above is a detailed explanation of integer and floating-point data storage , And includes the size of the end of the storage and the original code inverse complement and other details , If you don't understand, you are welcome to ask questions ！