当前位置:网站首页>Krypton Factor purple book chapter 7 violent solution
Krypton Factor purple book chapter 7 violent solution
2022-07-05 23:07:00 【Porter hunter of the program】
Catalog
Title Description
Background
You have been employed by the organisers of a Super Krypton Factor Contest in which contestants have very high mental and physical abilities. In one section of the contest the contestants are tested on their ability to recall a sequenace of characters which has been read to them by the Quiz Master. Many of the contestants are very good at recognising patterns. Therefore, in order to add some difficulty to this test, the organisers have decided that sequences containing certain types of repeated subsequences should not be used. However, they do not wish to remove all subsequences that are repeated, since in that case no single character could be repeated. This in itself would make the problem too easy for the contestants. Instead it is decided to eliminate all sequences containing an occurrence of two adjoining identical subsequences. Sequences containing such an occurrence will be called “easy”. Other sequences will be called “hard”.
For example, the sequence ABACBCBAD is easy, since it contains an adjoining repetition of the subsequence CB. Other examples of easy sequences are:
- BB
- ABCDACABCAB
- ABCDABCD
Some examples of hard sequences are:
- D
- DC
- ABDAB
- CBABCBA
In order to provide the Quiz Master with a potentially unlimited source of questions you are asked to write a program that will read input lines from standard input and will write to standard output.
Input description
Each input line contains integers nn and LL (in that order), where n>0n>0 and LL is in the range 1≤L≤261≤L≤26. Input is terminated by a line containing two zeroes.
Output description
For each input line prints out the nn-th hard sequence (composed of letters drawn from the first LL letters in the alphabet), in increasing alphabetical order (Alphabetical ordering here corresponds to the normal ordering encountered in a dictionary), followed (on the next line) by the length of that sequence. The first sequence in this ordering is ‘A’. You may assume that for given nn and LL there do exist at least nn hard sequences.
As such a sequence is potentially very long, split it into groups of four (4) characters separated by a space. If there are more than 16 such groups, please start a new line for the 17th group.
Your program may assume a maximum sequence length of 80.
For example, with L=3L=3, the first 7 hard sequences are:
A
AB
ABA
ABAC
ABACA
ABACAB
ABACABA
The sample input
7 3
30 3
0 0
Sample output
ABAC ABA
7
ABAC ABCA CBAB CABA CABC ACBA CABA
28
The main idea of the topic
Enter a n and L, From before L A difficult string of letters ( Adjacent ones do not have the same string ), Sort in dictionary order , Output No n A difficult string .
Ideas
Recursive deep search , Add judgment , Judge the time, just judge the suffix , The previous part has determined that the conditions are met , Just judge the later .
AC Code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N = 1e5+10;
int n,l,cnt;
int a[N];
int dfs(int t)
{
if(cnt++ == n){// Already found No n individual
for(int i = 0;i < t;i++)// Output time pay attention to the format required by the topic
{
if(i%4 == 0 && i != 0 && i%64 != 0)
cout << " ";
else if(i != 0 && i%64 == 0)
cout << endl;
printf("%c", 'A'+a[i]);
}
if(t%64 != 0)
cout << endl;
cout << t << endl;
return 0;
}
for(int i = 0;i < l;i++){// Deep search traversal
a[t] = i;
int flag = 1;
for(int j = 1;j*2 <= t+1;j++){// Judge whether the conditions of difficult string are met
int flag1 = 1;
for(int k = 0;k <j;k++){
if(a[t-k] != a[t-j-k]){
flag1 = 0;
break;
}
}
if(flag1)
{
flag = 0;
break;
}
}
/*
Judgment method : From the end , If the last one is not equal to the one adjacent to the front, the first one is satisfied ,
Secondly, make two judgments at intervals , In turn , Judge whether there is dissatisfaction .
Because it has been judged before , So each one only needs to be sentenced once .
*/
if(flag){
if(!dfs(t+1))//!dfs The representative found it and returned 0
return 0;
}
}
return 1;
}
int main()
{
while(cin >> n >> l){
cnt = 0;
if(n == 0 && l == 0){
return 0;
}
dfs(0);
}
}
Be careful
Particular attention : Format problem , The title clearly states , Every time 4 One for a group , One line at a time 16 Group , Output length time , If there happens to be one last 16 There is no need to wrap a group , If not , Need to output a newline .
边栏推荐
- Arduino measures AC current
- Southeast Asia e-commerce guide, how do sellers layout the Southeast Asia market?
- 2022 G3 boiler water treatment simulation examination and G3 boiler water treatment simulation examination question bank
- Global and Chinese markets of tantalum heat exchangers 2022-2028: Research Report on technology, participants, trends, market size and share
- Event trigger requirements of the function called by the event trigger
- Boring boring
- CorelDRAW plug-in -- GMS plug-in development -- new project -- macro recording -- VBA editing -- debugging skills -- CDR plug-in (2)
- Use the rewrite rule to rewrite all accesses to the a domain name to the B domain name
- Composition of interface
- 数据库基础知识(面试)
猜你喜欢
Thoroughly understand JVM class loading subsystem
一文搞定JVM常见工具和优化策略

SPSS analysis of employment problems of college graduates
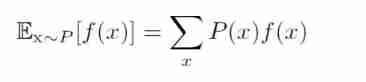
Expectation, variance and covariance
Go语言实现原理——锁实现原理
Using LNMP to build WordPress sites
数据库基础知识(面试)
Ultrasonic sensor flash | LEGO eV3 Teaching

Hainan Nuanshen tea recruits warmhearted people: recruitment of the product experience recommender of Nuanshen multi bubble honey orchid single cluster

Nangou Gili hard Kai font TTF Download with installation tutorial
随机推荐
Common JVM tools and optimization strategies
数据库基础知识(面试)
Global and Chinese markets for welding products 2022-2028: Research Report on technology, participants, trends, market size and share
Masked Autoencoders Are Scalable Vision Learners (MAE)
Selenium+pytest automated test framework practice
Global and Chinese markets for children's amusement facilities 2022-2028: Research Report on technology, participants, trends, market size and share
判断二叉树是否为完全二叉树
[speech processing] speech signal denoising and denoising based on Matlab GUI low-pass filter [including Matlab source code 1708]
The method and principle of viewing the last modification time of the web page
Tensor attribute statistics
Starting from 1.5, build a micro Service Framework -- log tracking traceid
Use of shell:for loop
3 find the greatest common divisor and the least common multiple
Media query: importing resources
一文搞定class的微觀結構和指令
February 13, 2022 -5- maximum depth of binary tree
2022 registration examination for safety management personnel of hazardous chemical business units and simulated reexamination examination for safety management personnel of hazardous chemical busines
Un article traite de la microstructure et des instructions de la classe
Arduino 测量交流电流
视频标准二三事