当前位置:网站首页>伯努利分布,二项分布和泊松分布以及最大似然之间的关系(未完成)
伯努利分布,二项分布和泊松分布以及最大似然之间的关系(未完成)
2022-07-03 05:45:00 【code bean】
首先说伯努利试验

伯努利分布
伯努利试验说的是下面一种事件情况:在生活中,有一些事件的发生只有两种可能,发生或者不发生(或者叫成功或者失败),这些事件都可以被称为伯努利试验。
伯努利试验的概率分布称为伯努利分布(两点分布、0-1分布),如果记成功概率为p,则失败概率为q=1-p,则:
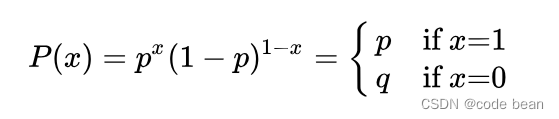
二项分布
假如某个试验是伯努利试验。进行n次这样的试验,成功了x次,则失败了n-x。二项分布认为:发生这种情况的概率可以用下面公式来计算:

二项分布的概率质量函数可以简写为X~B(n,p)。
实际上,当n = 1时,二项分布就是 伯努利分布。这就是二项分布和伯努利分布的关系。

所以这里我们可以看到,二项分布是一个离散的分布的直方图。X轴为成功次数,Y轴对应的是成功n次数概率值。

随着实验次数的递增,我们将得到一个类似正态分布的直方图。
一个有趣的例子(关于二项分布)

他将的是如果你去京东购物,你想买一款自行车,然后淘了三家店铺,第一家店铺共条10条评论,都是好评。第二家,50条评论,96%的好评,第三家,200条评论96%的好评。那我应该选哪家店进行购买。这里我假设一个前提,假设自行车质量OK的概率是x(质量NG的概率是1-x),当买家买到OK的自行车就会给出好评,否则差评。
那么看第一家,10条评论,都是好评。那么能说明第一家的自行车良品率是100%吗?不一定吧。我们假设第一家自行车的良品率是0.95。那么每次抽取10自行车都为OK的概率其实还挺高的(相当于10个顾客买到都OK自行车的概率)。
下图表示,如果自行车的良品率是0.95,每次抽10辆,分别抽取7,8,9,10辆是OK的概率。

也就是说,虽然10条评论,都是好评。但是自行车的OK率也是不确定的。但是根据这个二项分布,你说这家店的良品率在0.95左右,感觉还是可以的。总的来说样本太少,可能的情况很多。
也就是说,如果前确定了良品率,可以看到好评率的概率
 比如,如果良品率是0.95,那么如果有50条评论,其中有48条是好评的概率是0.26110(出现47条或49条好评也在0.2以上)
比如,如果良品率是0.95,那么如果有50条评论,其中有48条是好评的概率是0.26110(出现47条或49条好评也在0.2以上)
那么反过来,如果我们已知了一个好评的二项分布,能不能推出最有可能的良品率?那么其实分布和良品率s有对应的关系。
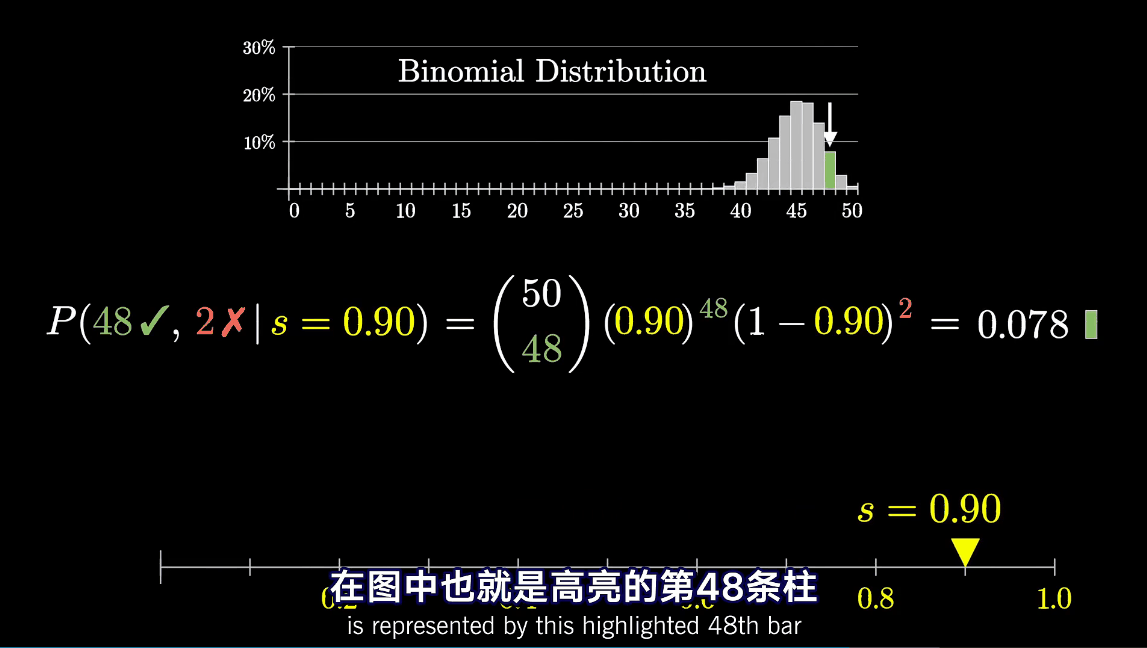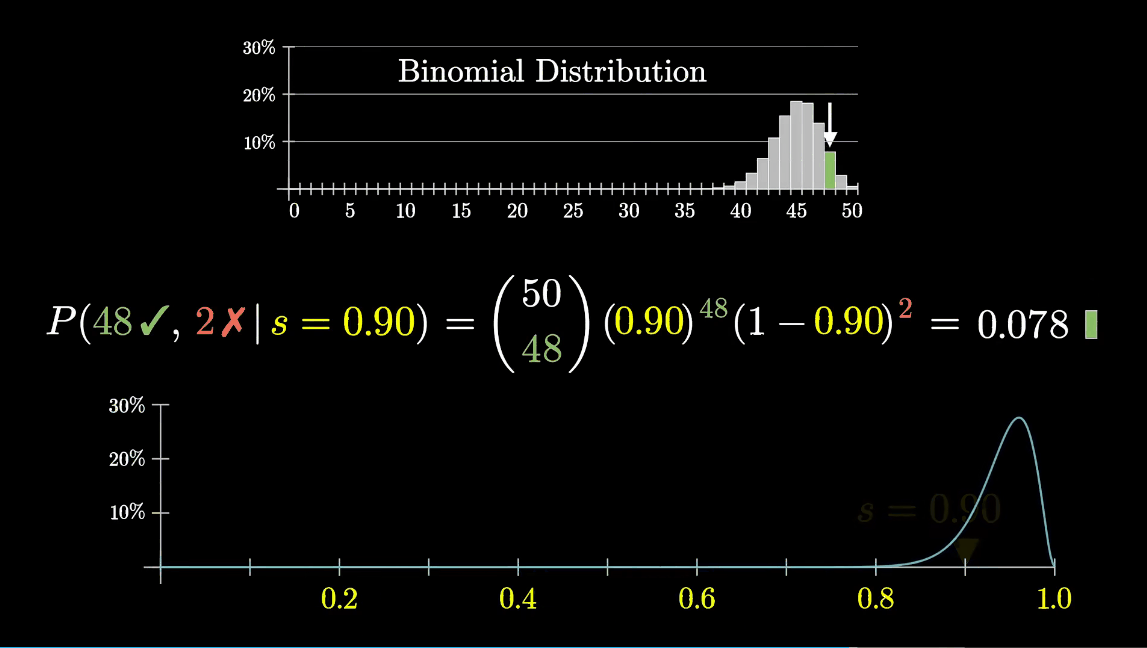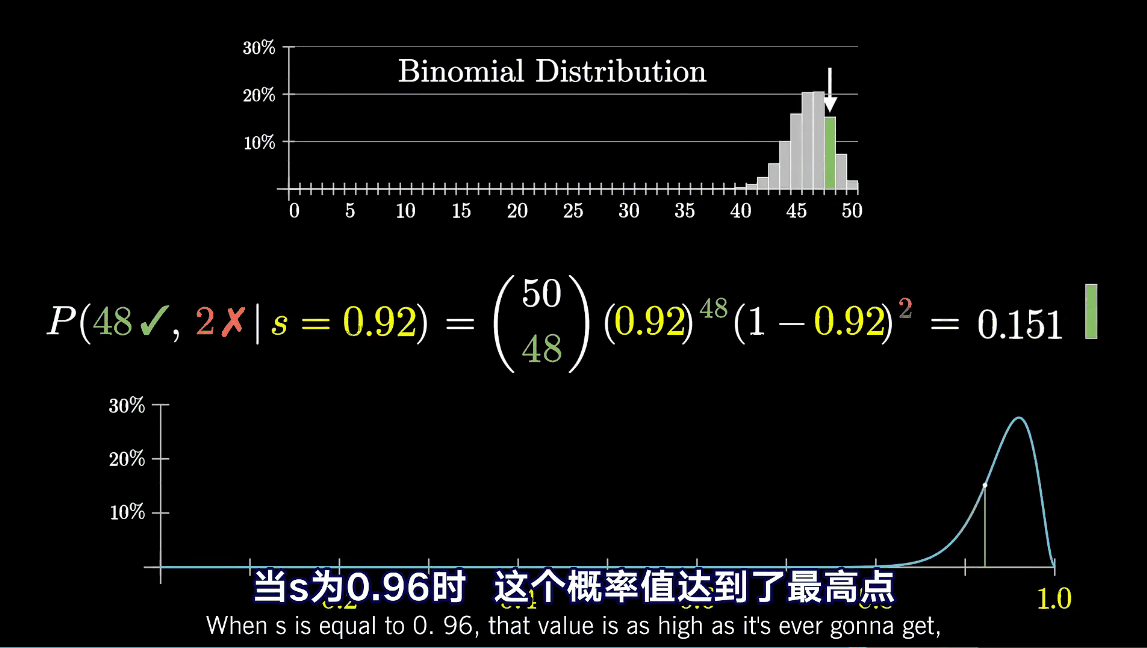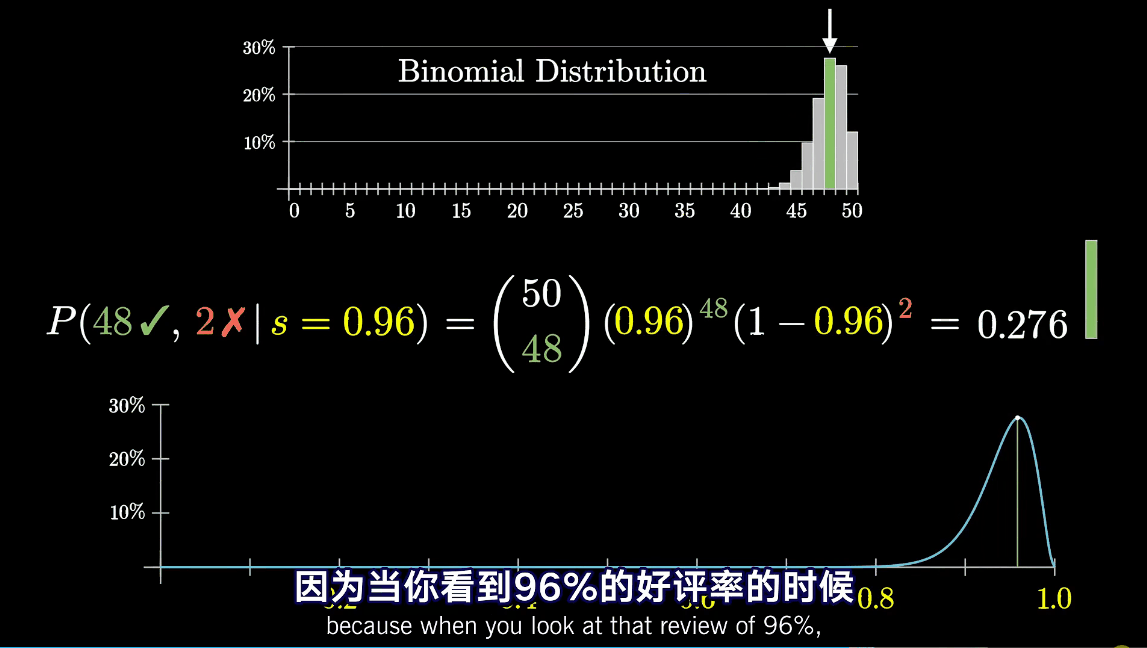
这个图说明,当s为0.96的时候,50条评论中出现48条好评的概率最大。
阶段小结:从这个例子中,我联想到了,先验概率,后验概率,最大似然(根据既定的事实推出概率模型),甚至联系到泊松分布。
这些貌似还和朴素贝叶斯有关,目前这部分的讨论就到这里吧,以后慢慢完成知识体系。
泊松分布

首先泊松分布是二项式分布的一种特殊形式,当二项式分布公式的p趋近0(很小),实验次数趋近无穷大,且n*p等于一个常量时,我们将得到泊松分布。泊松分布中的 “入”其实就是二项式分布中的n*p。
适用泊松分布的事件需要满足三个条件:
1 这个事件是一个小概率事件
2 事件独立互不影响
3 事件的概率稳定
将一定的时间无限划分,直至在时间上某事件最多发生一次。那么这段时间我称之为泊松分布的单位时间。
题目1: 目前一分钟钟来了3辆车,求一分钟来5辆车的概率?

当“入”确定之后,这个图像就确定了,概率P随着K的变化而变化。而在二项分布中需要知道n和p
这个“入”的含义是,在单位时间内随机事件的平均发生率(没错就是np了np的含义就是期望/均值)
题目2: 新华书店,每周卖出4本新华字典,老板应该备多少新华字典?(未完成)
参考资料:
统计学与质量026 - 伯努利试验及概率方程 二项式分布 期望值与方差_哔哩哔哩_bilibili
边栏推荐
- 卷积神经网络CNN中的卷积操作详解
- Azure file synchronization of altaro: the end of traditional file servers?
- [branch and cycle] | | super long detailed explanation + code analysis + a trick game
- Notepad++ wrap by specified character
- Calculation method of AUC
- [together Shangshui Shuo series] day 7 content +day8
- Niuke JS separator
- Final review (Day7)
- redis 遇到 NOAUTH Authentication required
- How does win7 solve the problem that telnet is not an internal or external command
猜你喜欢

Map的扩容机制
![[teacher Zhao Yuqiang] RDB persistence of redis](/img/cc/5509b62756dddc6e5d4facbc6a7c5f.jpg)
[teacher Zhao Yuqiang] RDB persistence of redis
![[set theory] relational closure (reflexive closure | symmetric closure | transitive closure)](/img/c8/2995c503e9dabae4e2cc704449e04f.jpg)
[set theory] relational closure (reflexive closure | symmetric closure | transitive closure)
![[escape character] [full of dry goods] super detailed explanation + code illustration!](/img/33/ec5a5e11bfd43f53f2767a9a0f0cc9.jpg)
[escape character] [full of dry goods] super detailed explanation + code illustration!
![[teacher Zhao Yuqiang] kubernetes' probe](/img/cc/5509b62756dddc6e5d4facbc6a7c5f.jpg)
[teacher Zhao Yuqiang] kubernetes' probe

QT read write excel -- qxlsx insert chart 5

【一起上水硕系列】Day 7 内容+Day8

Final review (Day5)
![[explain in depth the creation and destruction of function stack frames] | detailed analysis + graphic analysis](/img/df/884313a69fb1e613aec3497800f7ba.jpg)
[explain in depth the creation and destruction of function stack frames] | detailed analysis + graphic analysis
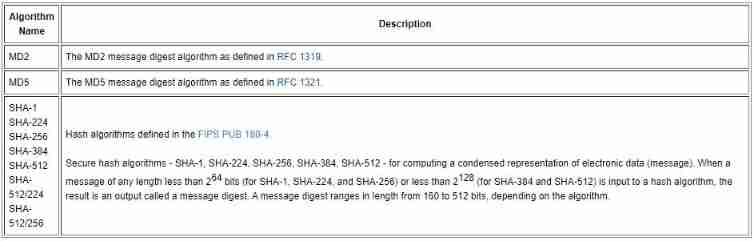
Understand one-way hash function
随机推荐
32GB Jetson Orin SOM 不能刷机问题排查
Common exceptions when Jenkins is released (continuous update...)
Mapbox tasting value cloud animation
Es 2022 officially released! What are the new features?
[teacher Zhao Yuqiang] redis's slow query log
PHP笔记超详细!!!
Get and monitor remote server logs
期末复习(DAY7)
Can altaro back up Microsoft teams?
Apache+PHP+MySQL环境搭建超详细!!!
Apt update and apt upgrade commands - what is the difference?
Ansible firewall firewalld setting
EMD distance - example of use
Complete set of C language file operation functions (super detailed)
Kubernetes resource object introduction and common commands (V) - (configmap)
2022.7.2 simulation match
[function explanation (Part 1)] | | knowledge sorting + code analysis + graphic interpretation
[untitled]
Altaro VM backup getting started
Configure DTD of XML file