当前位置:网站首页>优先级队列(堆)
优先级队列(堆)
2022-07-05 08:46:00 【牧..】
文章目录
优先级队列(堆)
前言
在学习 堆之前,我们 回忆 一下 二叉树的 存储方式,
我们之前学习的 二叉树 是不是 链式 存储 以 left 和 right 连接起来
而接下来我们 学习的 堆 就是 顺序存储 一颗二叉树表示的。
二叉树的顺序存储
存储方式
使用数组保存二叉树结构,方式即将二叉树用层序遍历方式放入数组中。
一般只适合表示完全二叉树,因为非完全二叉树会有空间的浪费。
这种方式的主要用法就是堆的表示
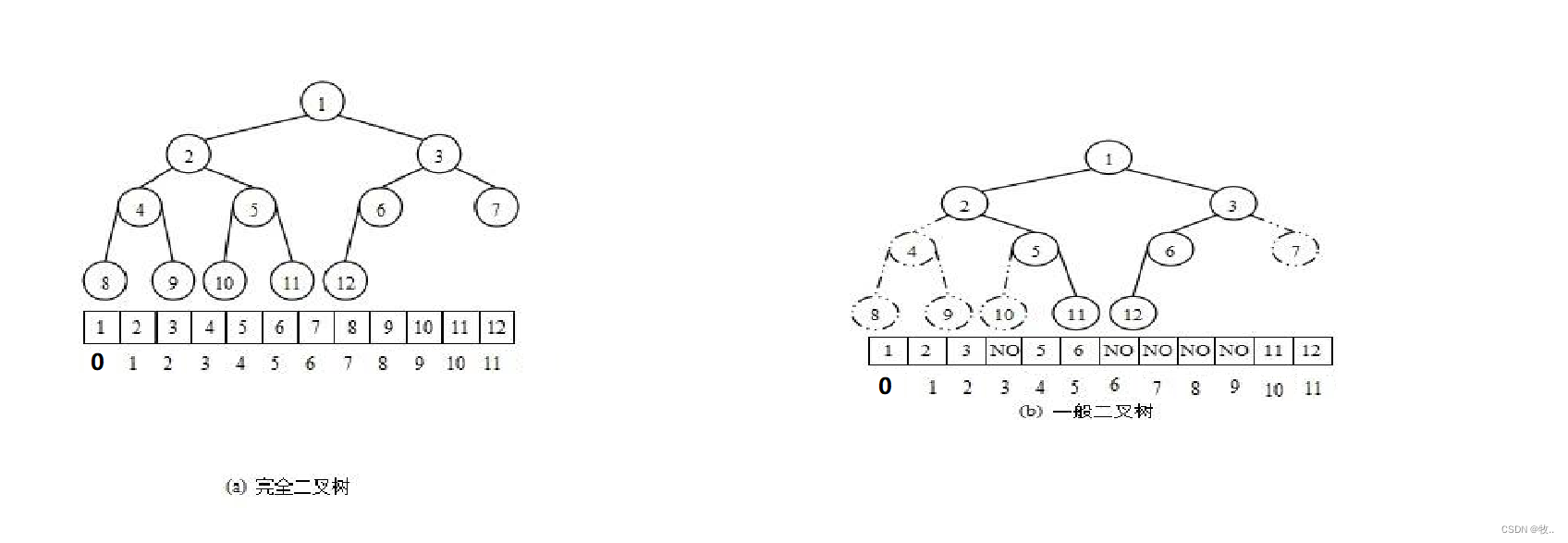
下标关系
已知双亲(parent)的下标,则:
左孩子(left)下标 = 2 * parent + 1;
右孩子(right)下标 = 2 * parent + 2;
已知孩子(不区分左右)(child)下标,则:
双亲(parent)下标 = (child - 1) / 2;
堆(heap)
概念
堆逻辑上是一棵完全二叉树
堆物理上是保存在数组中
满足任意结点的值都大于其子树中结点的值,叫做大堆,或者大根堆,或者最大堆
反之,则是小堆,或者小根堆,或者最小堆
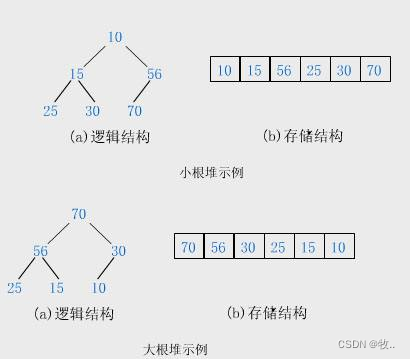
- 每颗二叉树的根节点都小于 左右孩子结点,
(小根堆/最小堆)
附上代码
public class TestHeap {
public int[] elem;
public int usedSize;
public TestHeap(){
this.elem = new int[10];
}
/** * 向下调整函数 实现 * @param parent 每棵树的根结点 * @param len 每棵树的调整结束位置 */
public void shifDown(int parent,int len) {
int child = 2 * parent + 1;
//1 最起码 有一个孩子 (左孩子)
while(child < len) {
// 9 + 1 == 10 那么就进入不了 循环
if(child + 1< len && elem[child] < elem[child+1]) {
child++;
}
if(elem[parent] < elem[child]) {
int tmp = elem[parent];
elem[parent] = elem[child];
elem[child] = tmp;
parent = child;
child = 2 * parent + 1;
}else {
break;
}
}
}
// 交换完成后需要继续向下 检测
public void createHeap(int[] array) {
for(int i = 0;i<array.length;i++) {
elem[i] = array[i];
this.usedSize++;
}
for(int parent = (usedSize - 1-1)/2;parent >= 0;parent--) {
// 调整
shifDown(parent,usedSize);
}
}
}
建立完 大根堆 ,接下来我们 来看一下 建堆的时间复杂度
但是 建堆的时间复杂度 为 O(n),下面 文章说明了,可以去看看
堆排序中建堆过程时间复杂度O(n)怎么来的?
建立小堆只需要 在 建立大堆的基础上 改一下即可
附上代码
public void shifDown2(int parent,int len) {
int child = 2 * parent + 1;
while(child < len) {
if(child + 1 < len && elem[child] > elem[child +1]) {
child++;
}
if(elem[parent] > elem[child]) {
int tmp = elem[parent];
elem[parent] = elem[child];
elem[child] = tmp;
parent = child;
child = 2 * parent + 1;
}else {
break;
}
}
}
堆应用 - 优先级 队列
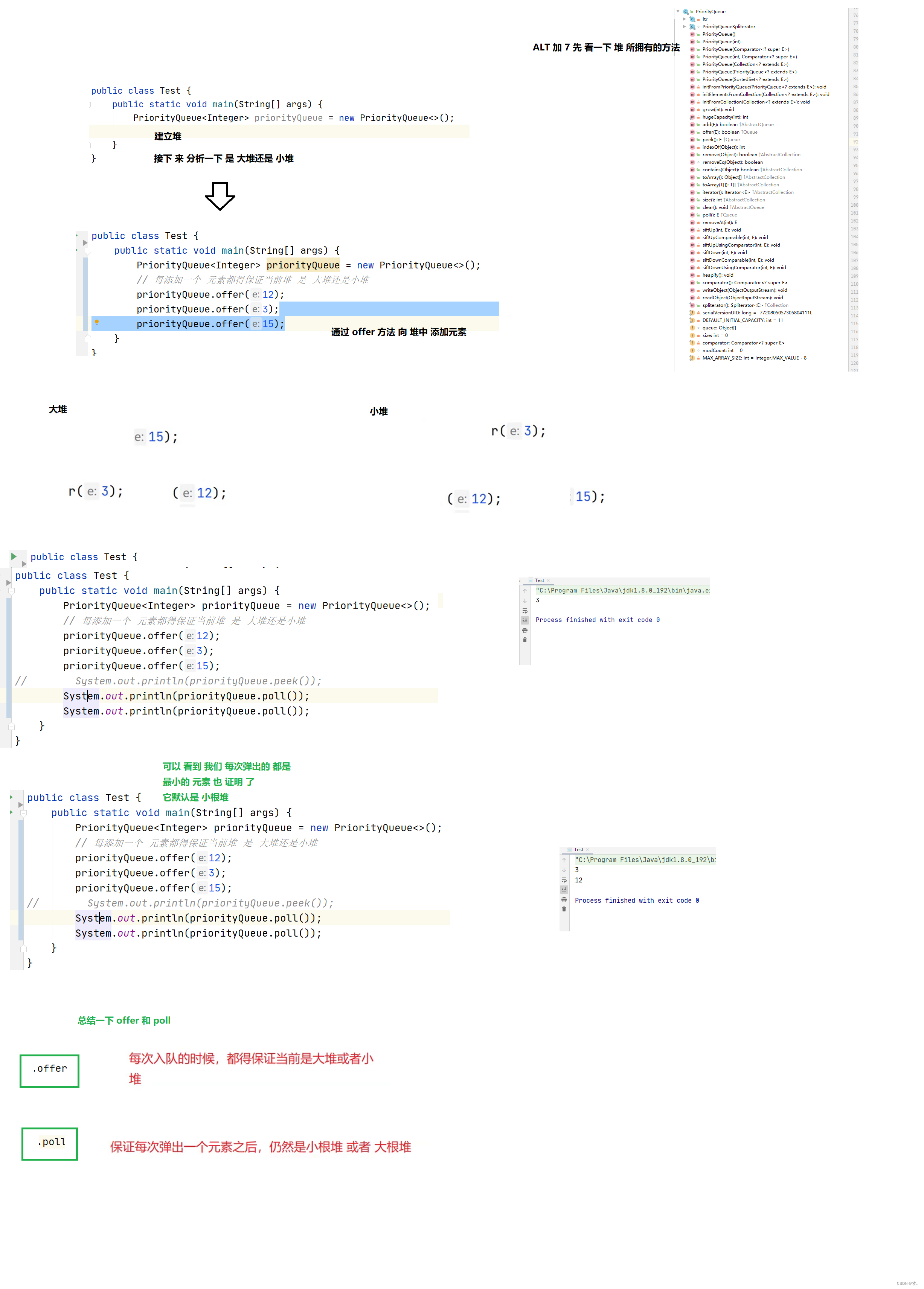
入堆 操作 offer
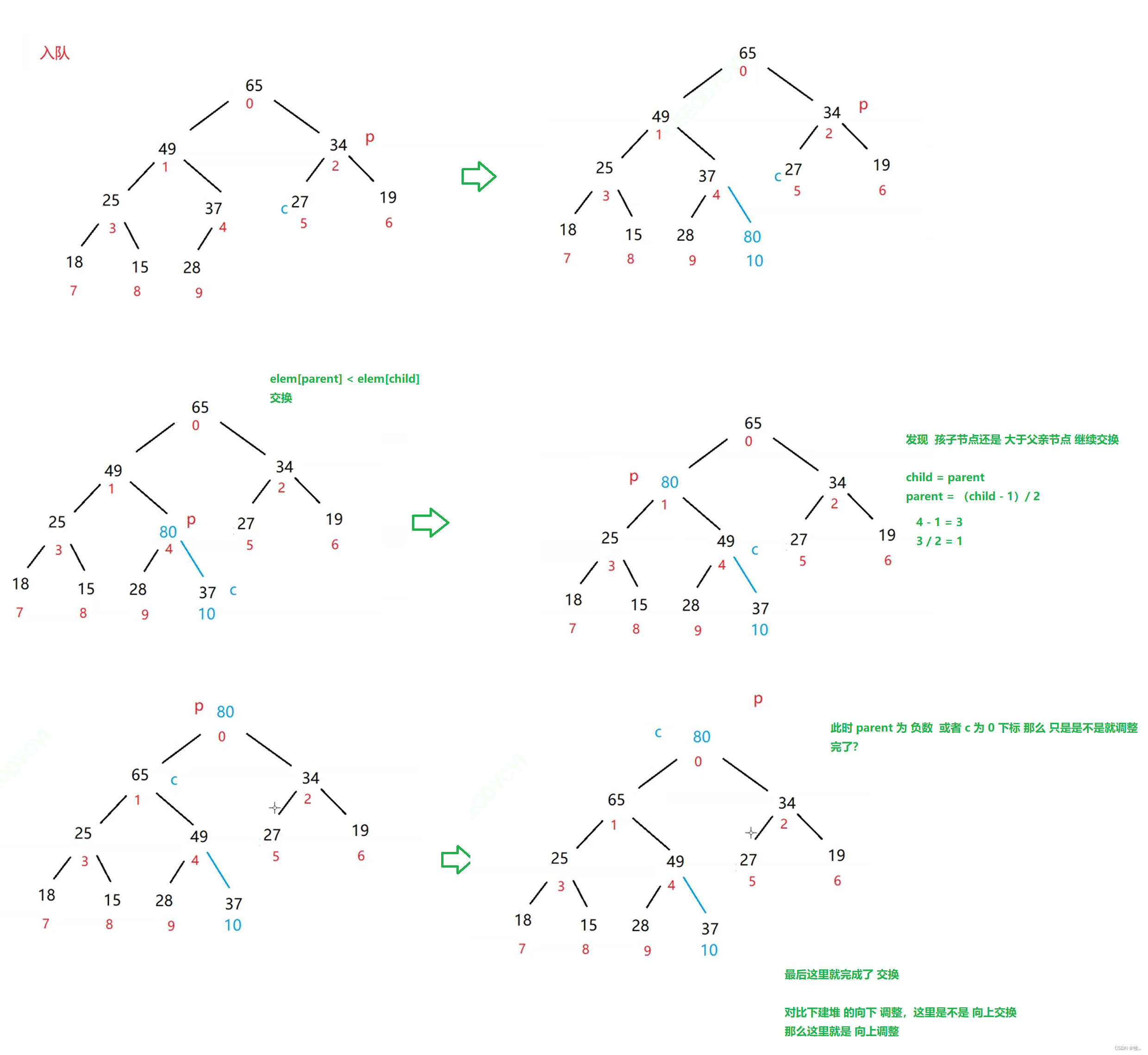
private void shiftUp(int child) {
int parent = (child - 1) / 2;
while(child != 0) {
if(elem[parent] < elem[child]) {
int tmp = elem[parent];
elem[parent] = elem[child];
elem[child] = tmp;
child = parent;
parent = (child - 1) / 2;
}else {
break;
}
}
}
public void offer(int val) {
if(isFull()) {
// 扩容
elem = Arrays.copyOf(elem,2 * elem.length);
}
elem[usedSize++] = val;
// 注意 这里 传入的参数 usedSize - 1
shiftUp(usedSize - 1);
}
public boolean isFull() {
return usedSize == elem.length;
}
可以看到我们 入队并且我成了 交换
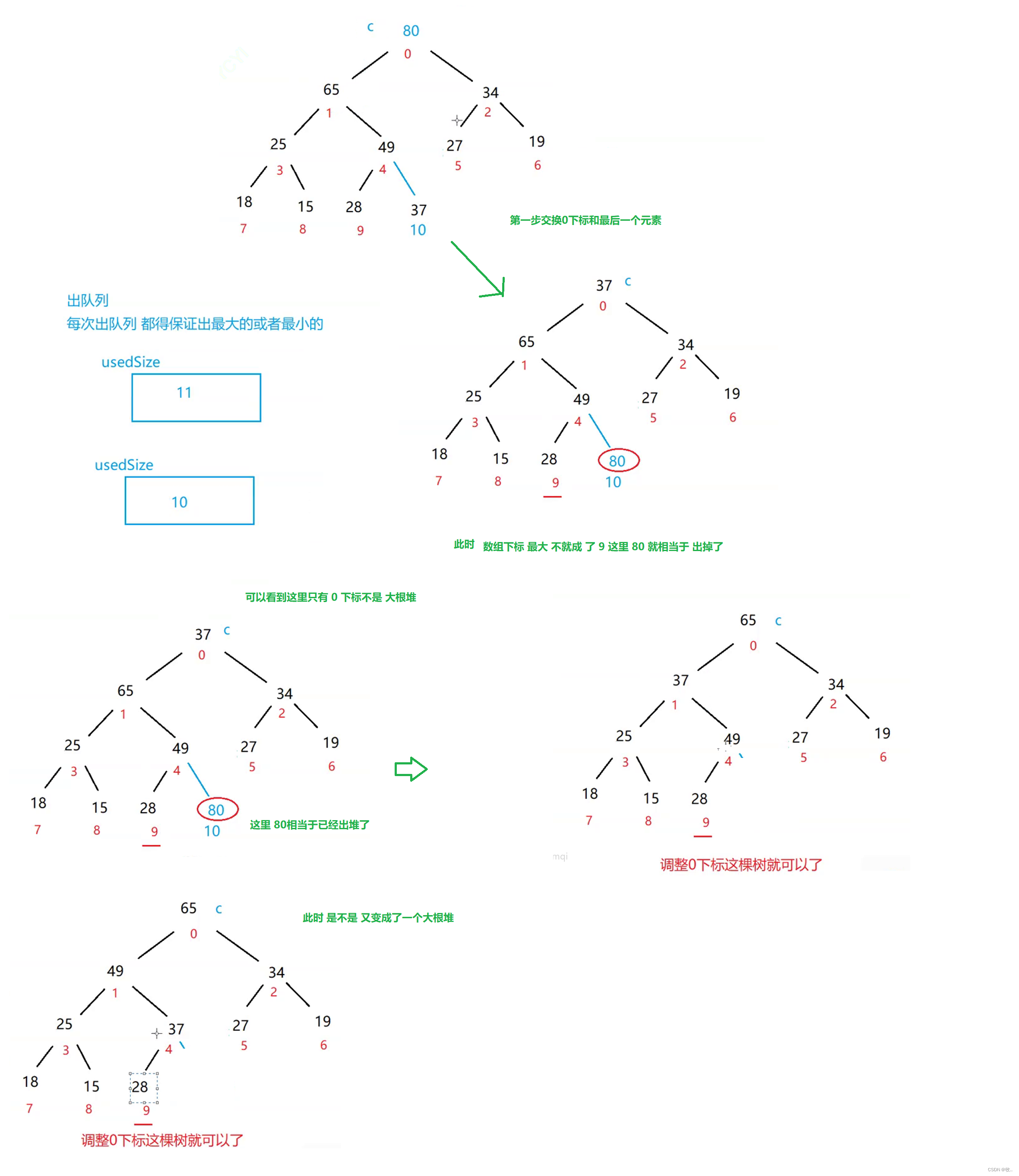
出堆操作 poll
附上代码
public class TestHeap {
public int[] elem;
public int usedSize;
public TestHeap(){
this.elem = new int[10];
}
/** * 向下调整函数 实现 * @param parent 每棵树的根结点 * @param len 每棵树的调整结束位置 */
public void shifDown(int parent,int len) {
int child = 2 * parent + 1;
//1 最起码 有一个孩子 (左孩子)
while(child < len) {
// 9 + 1 == 10 那么就进入不了 循环
if(child + 1< len && elem[child] < elem[child+1]) {
child++;
}
if(elem[parent] < elem[child]) {
int tmp = elem[parent];
elem[parent] = elem[child];
elem[child] = tmp;
parent = child;
child = 2 * parent + 1;
}else {
break;
}
}
}
// 交换完成后需要继续向下 检测
public void createHeap(int[] array) {
for(int i = 0;i<array.length;i++) {
elem[i] = array[i];
this.usedSize++;
}
for(int parent = (usedSize - 1-1)/2;parent >= 0;parent--) {
// 调整
shifDown(parent,usedSize);
}
}
private void shiftUp(int child) {
int parent = (child - 1) / 2;
while(child != 0) {
if(elem[parent] < elem[child]) {
int tmp = elem[parent];
elem[parent] = elem[child];
elem[child] = tmp;
child = parent;
parent = (child - 1) / 2;
}else {
break;
}
}
}
public void offer(int val) {
if(isFull()) {
// 扩容
elem = Arrays.copyOf(elem,2 * elem.length);
}
elem[usedSize++] = val;
// 注意 这里 传入的参数 usedSize - 1
shiftUp(usedSize - 1);
}
public boolean isFull() {
return usedSize == elem.length;
}
// 出堆操作
public int poll() {
if(isEmpty()) {
throw new RuntimeException("优先级队列为空 !");
}
// 交换 0 下标和 最后 一个元素
int tmp = elem[0];
elem[0] = elem[usedSize-1];
elem[usedSize-1] = tmp;
usedSize--;
// 调整 0 下标元素
shifDown(0,usedSize);
return tmp;
}
public boolean isEmpty() {
return usedSize == 0;
}
}
Topk问题非代码实现
接下俩 先来了解一下 topk 问题
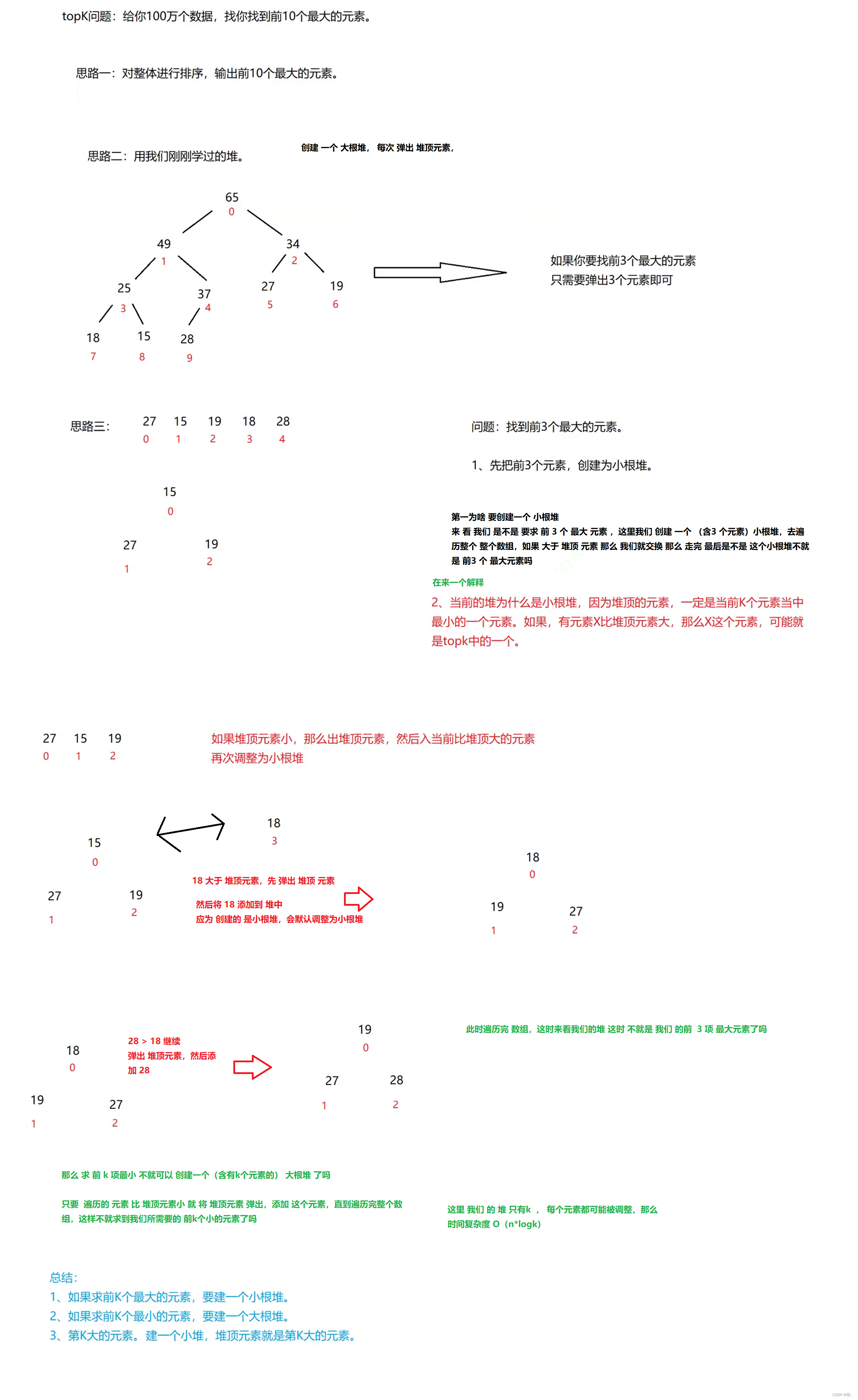
我们 先来 学习一下堆排序,学习完,我们才能更好的理解 有关 topk问题 的oj题 、
堆排序
接下来我们 来代码实现
public void shifDown(int parent,int len) {
int child = 2 * parent + 1;
//1 最起码 有一个孩子 (左孩子)
while(child < len) {
// 9 + 1 == 10 那么就进入不了 循环
if(child + 1< len && elem[child] < elem[child+1]) {
child++;
}
if(elem[parent] < elem[child]) {
int tmp = elem[parent];
elem[parent] = elem[child];
elem[child] = tmp;
parent = child;
child = 2 * parent + 1;
}else {
break;
}
}
}
public void heapSort() {
int end = usedSize - 1;
while(end > 0) {
int tmp = elem[0];
elem[0] = elem[end];
elem[end] = tmp;
shifDown(0,end);
end--;
}
}
分析完 在些代码是不是非常简单
接下来我们 来 完成
优先级队列插入元素
优先级队列在插入元素时有个要求:插入的元素不能是null或者元素之间必须要能够进行比较,为了简单起见,我们只是插入了Integer类型,那优先级队列中能否插入自定义类型对象呢?

插入 ,和交换操作 的 源码 分析
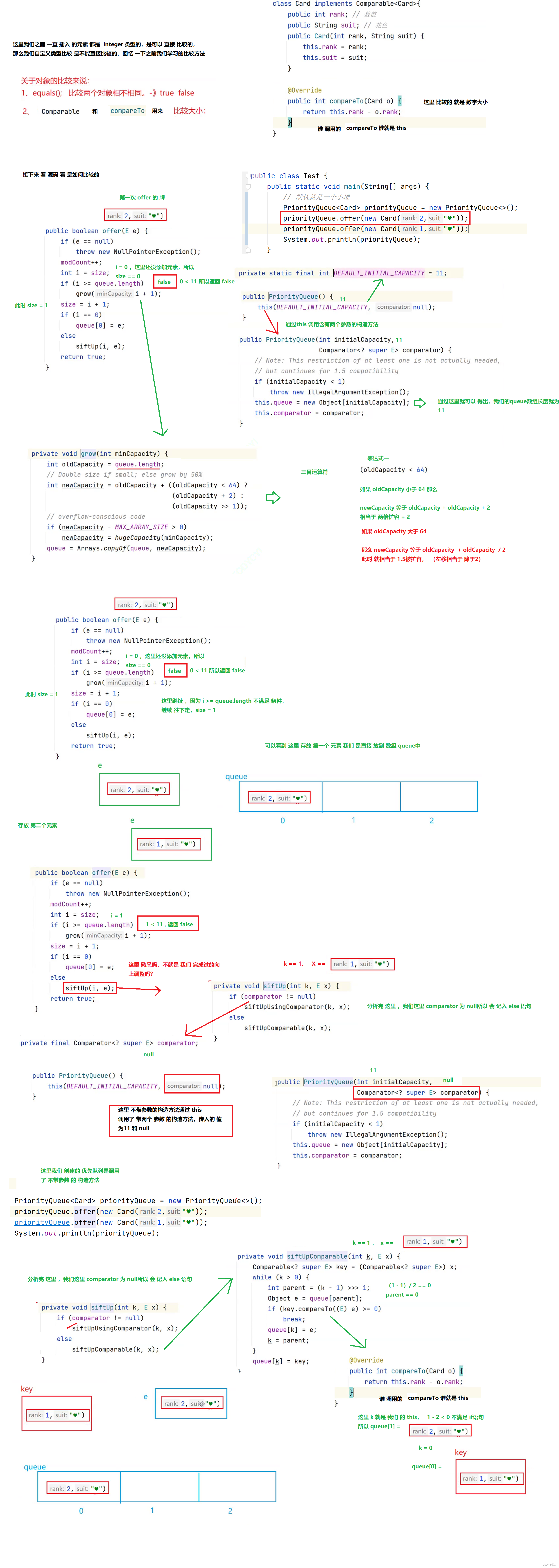
附上代码
class Card implements Comparable<Card> {
public int rank; // 数值
public String suit; // 花色
public Card(int rank, String suit) {
this.rank = rank;
this.suit = suit;
}
@Override
public int compareTo(Card o) {
return this.rank - o.rank;
//这里 换成 0.rank - this.rank,就换成了 大堆
}
@Override
public String toString() {
return "Card{" +
"rank=" + rank +
", suit='" + suit + '\'' +
'}';
}
}
public class Test {
public static void main(String[] args) {
// 默认就是一个小堆
PriorityQueue<Card> priorityQueue = new PriorityQueue<>();
priorityQueue.offer(new Card(2,""));
priorityQueue.offer(new Card(1,""));
System.out.println(priorityQueue);
}
}
回忆一下 Comparable 接口 ,他是不是 对类侵入性太强, 一旦写好了,根据那种规则比较那么就不能轻易进行修改了。
那么这里 我 们就 可以 使用 单独的 写 一些比较器。
class RankComparator implements Comparator<Card> {
@Override
public int compare(Card o1, Card o2) {
return o1.rank - o2.rank;
}
}
public class Test {
public static void main(String[] args) {
Card card1 = new Card(1,"");
Card card2 = new Card(2,"");
RankComparator rankComparator = new RankComparator();
int ret = rankComparator.compare(card1,card2);
System.out.println(ret);
}
}
回忆完这些,那么 我们 使用优先级队列是不是 可以 ,传入比较器来完成比较的呢。这里显然是可以的
public class Test {
public static void main(String[] args) {
RankComparator rankComparator = new RankComparator();
Card card1 = new Card(1,"");
Card card2 = new Card(2,"");
// 直接传入 比较器
PriorityQueue<Card> priorityQueue = new PriorityQueue<>(rankComparator);
priorityQueue.offer(card1);
priorityQueue.offer(card2);
System.out.println(priorityQueue);
}
}
这里 除了 比较器 和 使用Comparable 中 compareTo 方法比较之外还能这样写
public static void main(String[] args) {
RankComparator rankComparator = new RankComparator();
Card card1 = new Card(1,"");
Card card2 = new Card(2,"");
PriorityQueue<Card> priorityQueue = new PriorityQueue<>(new Comparator<Card>() {
@Override
public int compare(Card o1, Card o2) {
return o1.rank - o2.rank;
}
});
priorityQueue.offer(card1);
priorityQueue.offer(card2);
System.out.println(priorityQueue);
}
这里 就不需要 创建 比较器 也能比较,
这里 就相当于 一个内部类,重写了 compare方法。
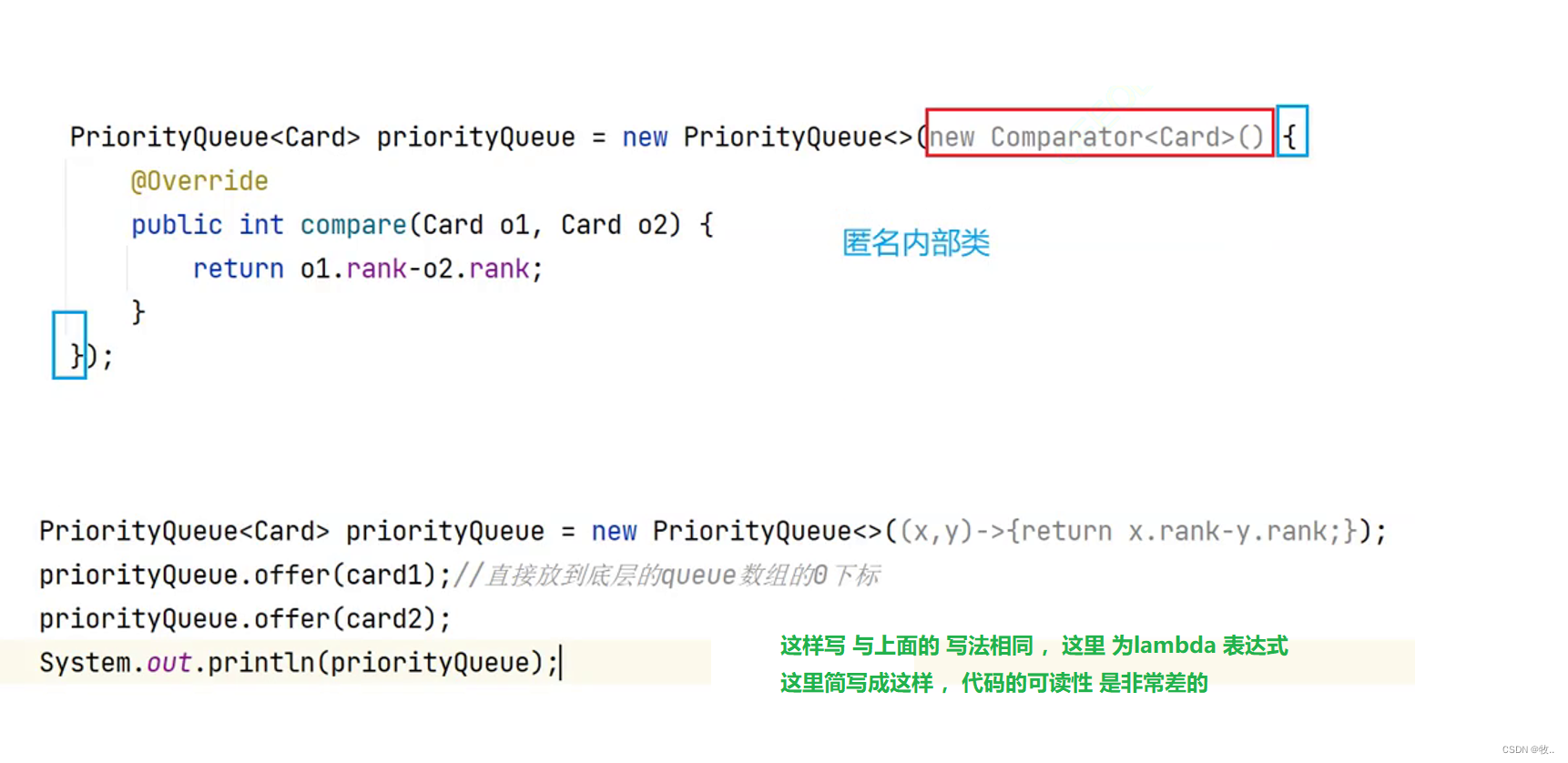
除了以上 这些方法 我们 还可以通过重写 equals 方法来进行比较
三种比较方式 区别

Topk 问题 代码实现
上面 我们 已经分析完 Topk 的 思路 ,这里 代码实现
public class Topk2 {
/** * 求数组中的前K 个最小的元素 * @param array * @param k * @return * 采用 大根堆 */
public static int[] topk(int[] array,int k){
// 1.创建一个大小为k 的大根堆
PriorityQueue<Integer> maxHeap = new PriorityQueue<>(k, new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
// 这样比较就为大堆
return o2 - o1;
}
});
// 2.遍历数组当中的元素,前k个元素放到堆中
for(int i = 0;i<array.length;i++){
if(maxHeap.size() < k) {
maxHeap.offer(array[i]);
}else {
int tmp = maxHeap.peek();
if(tmp > array[i]) {
// 先弹出
maxHeap.poll();
// 在存入
maxHeap.offer(array[i]);
}
}
}
int[] arr = new int[k];
for(int i = 0;i < k;i++) {
arr[i] = maxHeap.poll();
}
return arr;
}
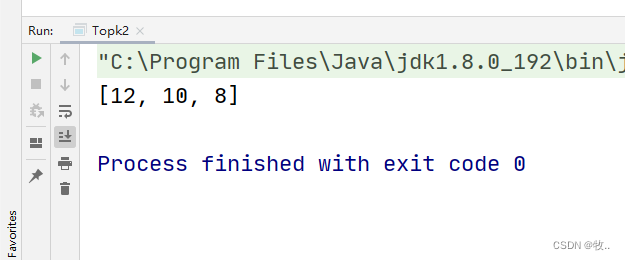
public static void main(String[] args) {
int[] array = {
18,21,8,10,34,12};
int[] ret = topk(array,3);
System.out.println(Arrays.toString(ret));
}
}
接下来就来完成一个 有关topk 的 oj 题
查找和最小的 K 对数字

class Solution {
public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
PriorityQueue<List<Integer>> maxHeap = new PriorityQueue<>(k, new Comparator<List<Integer>>() {
@Override
public int compare(List<Integer> o1, List<Integer> o2) {
// 创建大根堆 的比较方法
return (o2.get(0)+o2.get(1)) - (o1.get(0)+o1.get(1));
}
});
for(int i = 0;i< Math.min(k,nums1.length);i++) {
for(int j = 0;j< Math.min(k,nums2.length);j++) {
if(maxHeap.size() < k) {
List<Integer> tmpList = new ArrayList<>();
tmpList.add(nums1[i]);
tmpList.add(nums2[j]);
maxHeap.offer(tmpList);
}else {
int top = maxHeap.peek().get(0) + maxHeap.peek().get(1);
if(top > (nums1[i] + nums2[j])) {
List<Integer> tmpList = new ArrayList<>();
maxHeap.poll();
tmpList.add(nums1[i]);
tmpList.add(nums2[j]);
maxHeap.offer(tmpList);
}
}
}
}
List<List<Integer>> ret = new ArrayList<>();
// 这里 注意 k 如果 大于 数对 就要判断,堆是否为空
for(int i = 0;i<k && !maxHeap.isEmpty();i++) {
ret.add(maxHeap.poll());
}
return ret;
}
}
边栏推荐
- 图解网络:什么是网关负载均衡协议GLBP?
- How apaas is applied in different organizational structures
- 【日常訓練--騰訊精選50】557. 反轉字符串中的單詞 III
- Guess riddles (7)
- Guess riddles (6)
- Golang foundation -- map, array and slice store different types of data
- 图解八道经典指针笔试题
- [daiy4] copy of JZ35 complex linked list
- ROS learning 4 custom message
- Ros-10 roslaunch summary
猜你喜欢

Halcon color recognition_ fuses. hdev:classify fuses by color
Halcon Chinese character recognition
Business modeling of software model | stakeholders
![[matlab] matlab reads and writes Excel](/img/80/78e4c7fcd27473526e480d4b930e2c.jpg)
[matlab] matlab reads and writes Excel

猜谜语啦(2)

How to manage the performance of R & D team?

Halcon snap, get the area and position of coins
![[daiy4] copy of JZ35 complex linked list](/img/bc/ce90bb3cb6f52605255f1d6d6894b0.png)
[daiy4] copy of JZ35 complex linked list
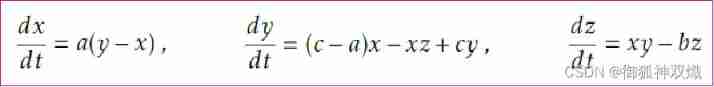
Solutions of ordinary differential equations (2) examples

IT冷知识(更新ing~)
随机推荐
EA introduction notes
c#比较两张图像的差异
How to manage the performance of R & D team?
12. Dynamic link library, DLL
C#图像差异对比:图像相减(指针法、高速)
AdaBoost use
Guess riddles (10)
多元线性回归(梯度下降法)
Multiple linear regression (sklearn method)
The combination of deep learning model and wet experiment is expected to be used for metabolic flux analysis
AUTOSAR从入门到精通100讲(103)-dbc文件的格式以及创建详解
Classification of plastic surgery: short in long long long
Beautiful soup parsing and extracting data
[formation quotidienne - Tencent Selection 50] 557. Inverser le mot III dans la chaîne
Characteristic Engineering
轮子1:QCustomPlot初始化模板
Halcon wood texture recognition
【日常训练--腾讯精选50】557. 反转字符串中的单词 III
location search 属性获取登录用户名
It cold knowledge (updating ing~)

