当前位置：网站首页>Binary tree
Binary tree
2022-07-07 23:11:00 【Yake1965】
Binary tree （Binary Tree）
- Binary search tree
- [501. The mode in the binary search tree ](https://leetcode.cn/problems/find-mode-in-binary-search-tree/)
- [ The finger of the sword Offer 54. The second of binary search tree k Big node ](https://leetcode.cn/problems/er-cha-sou-suo-shu-de-di-kda-jie-dian-lcof/)
- [ The finger of the sword Offer 36. Binary search tree and double linked list ](https://leetcode.cn/problems/er-cha-sou-suo-shu-yu-shuang-xiang-lian-biao-lcof/)
- [96. Different binary search trees ](https://leetcode.cn/problems/unique-binary-search-trees/)
- [95. Different binary search trees II](https://leetcode.cn/problems/unique-binary-search-trees-ii/)
- [ The finger of the sword Offer 34. The path of a value in a binary tree ](https://leetcode.cn/problems/er-cha-shu-zhong-he-wei-mou-yi-zhi-de-lu-jing-lcof/)
- [1609. Even tree ](https://leetcode-cn.com/problems/even-odd-tree/)
- 1609. Even tree
- 100. Same tree
- 101. Symmetric binary tree
- 104. The maximum depth of a binary tree
- 108. Convert an ordered array to a binary search tree
- 110. Balanced binary trees
- 111. Minimum depth of binary tree
- 230. Binary search tree K Small elements
- 559. N The maximum depth of the fork tree
- 563. The slope of the binary tree
- 671. The second smallest node in a binary tree
- 700. Search in binary search tree
- 863. All distances in a binary tree are K The node of
- 1104. Binary trees find their way
- Binary tree path
- 112. The sum of the paths
- 113. The sum of the paths II
- 257. All paths of binary tree
- 437. The sum of the paths III
- 988. The smallest string starting from the leaf node
Binary search tree
501. The mode in the binary search tree
The middle order traversal sequence of binary search tree is a non decreasing ordered sequence , The same number must be continuous .
class Solution {
List<Integer> ans = new ArrayList<>();
int base, cnt, max;
public int[] findMode(TreeNode root) {
dfs(root);
int[] res = new int[ans.size()];
for(int i = 0; i < ans.size(); i++) res[i] = ans.get(i);
return res;
}
void dfs(TreeNode node){
if(node == null) return;
dfs(node.left);
update(node.val);
dfs(node.right);
}
void update(int x){
if(x == base) cnt++;
else {
cnt = 1;
base = x;
}
if(cnt == max) ans.add(base);
else if(cnt > max){
max = cnt;
ans.clear();
ans.add(base);
}
}
}
use Morris The method of middle order traversal optimizes the space complexity of middle order traversal to O(1).
The finger of the sword Offer 54. The second of binary search tree k Big node
The middle order traversal of binary search tree is Increasing sequence , That is to say The middle order traverses the reverse order by Decreasing sequence .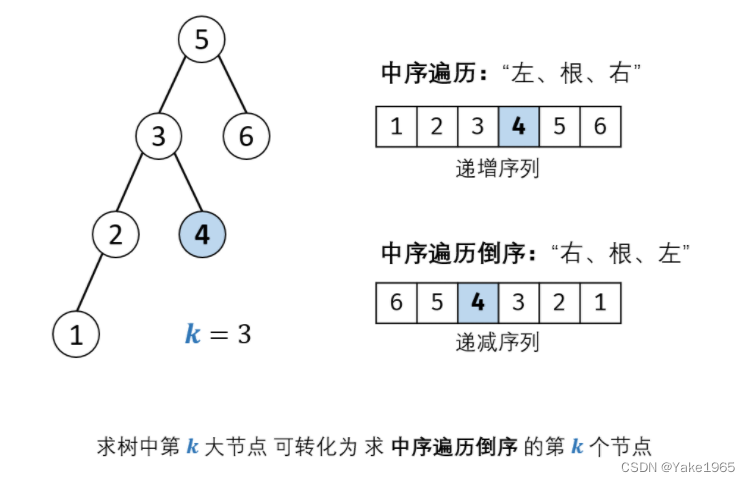
class Solution {
int k, ans = 0;
public int kthLargest(TreeNode root, int k) {
this.k = k;
dfs(root);
return ans;
}
void dfs(TreeNode root) {
if(root == null) return;
dfs(root.right);
if(--k == 0) {
ans = root.val; return;
}
dfs(root.left);
}
}
class Solution {
public int kthLargest(TreeNode root, int k) {
Deque<TreeNode> q = new ArrayDeque<>();
// while(q.size() > 0 || root != null){
while(true){
while(root != null){
q.push(root);
root = root.right;
}
root = q.pop();
if(--k == 0) return root.val;
root = root.left;
}
// return 0;
}
}
The finger of the sword Offer 36. Binary search tree and double linked list
class Solution {
Node pre, head;
public Node treeToDoublyList(Node root) {
if(root == null) return null;
dfs(root);
head.left = pre;
pre.right = head;
return head;
}
void dfs(Node cur){
if(cur == null) return;
dfs(cur.left);
if(pre != null) pre.right = cur;
else head = cur;
cur.left = pre;
pre = cur;
dfs(cur.right);
}
}
96. Different binary search trees
class Solution {
int[] a = new int[20]; // a[0] = 1; a[1] = 1;
public int numTrees(int n) {
if(n == 0 || n == 1) return 1; // Multiplying left and right requires t[0] = 1
if(a[n] > 0) return a[n];
int cnt = 0;
for (int i = 1; i <= n; i++) {
// With i Recurse around for the root , Multiply .
int left = numTrees(i-1);
int right = numTrees(n-i);
cnt += left * right;
}
a[n] = cnt;
return cnt;
}
}
95. Different binary search trees II
class Solution {
public List<TreeNode> generateTrees(int n) {
return f(1, n);
}
List<TreeNode> f(int s, int e){
List<TreeNode> ans = new LinkedList();
if(s > e){
ans.add(null);
return ans;
}
for(int i = s; i <= e; i++){
List<TreeNode> left = f(s, i - 1);
List<TreeNode> right = f(i + 1, e);
for(TreeNode l : left){
for(TreeNode r : right){
TreeNode cur = new TreeNode(i);
cur.left = l;
cur.right = r;
ans.add(cur);
}
}
}
return ans;
}
}
The finger of the sword Offer 34. The path of a value in a binary tree
class Solution {
List<List<Integer>> ans = new LinkedList<>();
Deque<Integer> path = new ArrayDeque<>();
public List<List<Integer>> pathSum(TreeNode root, int target) {
dfs(root, target);
return ans;
}
void dfs(TreeNode root, int target){
if(root == null) return;
path.add(root.val);
target -= root.val;
if(root.left == null && root.right == null && target == 0){
ans.add(new LinkedList<Integer>(path));
}
dfs(root.left, target);
dfs(root.right, target);
path.pollLast();
}
}
1609. Even tree
class Solution {
public boolean isEvenOddTree(TreeNode root) {
Deque<TreeNode> q = new LinkedList<>();
q.offer(root);
boolean even = true;
while(!q.isEmpty()){
int size = q.size(), pre = (even) ? 0 : 1000000;
// for(int i = 0; i < q.size(); i++){ // Can't be used directly q.size()
while(size-- > 0){
TreeNode node = q.poll();
int x = node.val;
if(even){
// Even subscript ,x Is even or decreasing
if(x % 2 == 0 || pre >= x) return false;
}
else{
// Odd subscript ,x Is odd or increasing
if(x % 2 == 1 || pre <= x) return false;
}
pre = x;
if(node.left != null) q.offer(node.left);
if(node.right != null) q.offer(node.right);
}
even = !even;
}
return true;
}
}
1609. Even tree
class Solution:
def isEvenOddTree(self, root: Optional[TreeNode]) -> bool:
q = deque([root])
even = True
while q:
pre = 0 if even else 1000000
for i in range(len(q)):
node = q.popleft()
x = node.val
if even:
if not x % 2 or x <= pre: return False
else:
if x % 2 or x >= pre: return False
pre = x
node.left and q.append(node.left)
node.right and q.append(node.right)
even = not even
return True
100. Same tree
class Solution:
def isSameTree(self, p: TreeNode, q: TreeNode) -> bool:
if not p and not q: return True
if not p or not q or p.val != q.val: return False
# return self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)
# Middle preface
stackP, stackQ, curP, curQ = [p], [q], p.left, q.left
while stackP or stackQ or curP or curQ:
if not curP and curQ or curP and not curQ: return False
while curP and curQ:
stackP.append(curP)
stackQ.append(curQ)
curP = curP.left
curQ = curQ.left
curP = stackP.pop()
curQ = stackQ.pop()
if curP.val != curQ.val:
return False
curP = curP.right
curQ = curQ.right
return True
101. Symmetric binary tree
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
# q = [root, root]
q = [(root, root)]
while q:
# u = q.pop()
# v = q.pop()
u, v = q.pop()
if not u and not v: continue
if not u or not v or u.val != v.val:
return False
# q.extend([u.left, v.right])
# q.extend([u.right, v.left])
q.append((u.left, v.right))
q.append((u.right, v.left))
return True
104. The maximum depth of a binary tree
Leetcode
The depth of a binary tree node ： Refers to the longest simple path from the root node to this node edge The article number .
The height of a binary tree node ： Refers to the longest simple path from this node to the leaf node edge The article number .
explain ：leetcode Define the node as one degree , The root node depth is 1; Wikipedia Define the edge as one degree , The depth of the root node is 0.
The depth can be checked from top to bottom , So we need preorder traversal （ Around the middle ）, And the height can only be checked from bottom to top , So it can only be traversed by postorder （ Right and left ）.
The former sequence traversal
class Solution:
def maxDepth(self, root: TreeNode) -> int:
def getDepth(node, depth):
nonlocal result
result = max(depth, result) # in
node.left and getDepth(node.left, depth + 1) # Left
node.right and getDepth(node.right, depth + 1) # Right
result = 0
if not root: return 0
getDepth(root, 1)
return result
The maximum depth of a binary tree , That is, the height of the root node , So you can also use post order traversal .
class Solution:
def maxDepth(self, root: TreeNode) -> int:
if not root: return 0
## bfs deque
# que = collections.deque([(root, 1)])
# while que:
# node, depth = que.popleft()
# res = depth # max(res, depth)
# node.left and que.append((node.left, depth + 1))
# node.right and que.append((node.right, depth + 1))
# return res # You don't need variables res, Go straight back to depth that will do .
## bfs list
q = [root]
res = 0
while q:
q = [child for node in q for child in [node.left, node.right] if child]
res += 1
return res
## dfs
# return max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1
# return max(self.maxDepth(node) for node in [root.left, root.right]) + 1
108. Convert an ordered array to a binary search tree
class Solution:
def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
if not nums: return None
mid = len(nums) // 2 # Select the value between
root = TreeNode(nums[mid])
if mid >= 1:
root.left = self.sortedArrayToBST(nums[:mid])
if mid < len(nums) - 1:
root.right = self.sortedArrayToBST(nums[mid+1:])
return root
110. Balanced binary trees
Leetcode
Balanced binary trees ： A binary tree, each node The absolute value of the height difference between the left and right subtrees is not more than 1 .
Method 1 ： Top down recursion
class Solution:
def isBalanced(self, root: TreeNode) -> bool:
# Maximum height of subtree
def height(root: TreeNode) -> int:
return max(height(root.left), height(root.right)) + 1 if root else 0
return not root or abs(height(root.left) - height(root.right)) <= 1 and self.isBalanced(root.left) and self.isBalanced(root.right)
Method 2 ： Bottom up recursion
class Solution:
def isBalanced(self, root: TreeNode) -> bool:
def height(root: TreeNode) -> int:
if not root: return 0
left = height(root.left)
right = height(root.right)
return -1 if left == -1 or right == -1 or abs(left - right) > 1 else max(left, right) + 1
return height(root) >= 0
111. Minimum depth of binary tree
Method 1 ： Depth-first search
class Solution:
def minDepth(self, root: TreeNode) -> int:
if not root: return 0
if not root.left and not root.right: return 1
min_depth = 10**9
if root.left:
min_depth = min(self.minDepth(root.left), min_depth)
if root.right:
min_depth = min(self.minDepth(root.right), min_depth)
return min_depth + 1
Method 2 ： Breadth first search
class Solution:
def minDepth(self, root: TreeNode) -> int:
if not root: return 0
que = collections.deque([(root, 1)])
while que:
node, depth = que.popleft()
if not node.left and not node.right: # leaf node
return depth
node.left and que.append((node.left, depth + 1))
node.right and que.append((node.right, depth + 1))
230. Binary search tree K Small elements
Method 1 ： In the sequence traversal
Binary search tree ：
- The left subtree of a node contains only the number less than the current node .
- The right subtree of a node contains only a number greater than the current node .
- All left and right subtrees themselves must also be binary search trees .
In the sequence traversal ：
Visit according to The left subtree — Root node — Right subtree Traversing the binary tree ; When accessing its left and right subtrees , Traverse in the same way ; Until you walk through the whole tree .
「 Middle order traversal of binary trees 」 Reference resources **「94. Official solution to the problem of traversing the middle order of binary trees 」**
Use iterative methods , This way you can stop when you find the answer , You don't need to traverse the whole tree .
class Solution:
def kthSmallest(self, root: TreeNode, k: int) -> int:
stack = []
while root or stack:
while root:
stack.append(root)
root = root.left
root = stack.pop()
k -= 1
if k == 0:
return root.val
root = root.right
Method 2 ： Record the node number of subtree
Record the number of nodes of the subtree with each node as the root node , Directly find the k Small value .
class Bst:
def __init__(self, root: TreeNode):
self.root = root
# Count the number of nodes of the subtree with each node as the root node , And stored in the hash table
self._node_num = {
}
self._count_node_num(root)
def kth_smallest(self, k: int):
""" Returns the... In the binary search tree k Small elements """
node = self.root
while node:
left = self._get_node_num(node.left)
if left < k - 1: # The left tree is not enough to add the right tree
node = node.right
k -= left + 1
elif left == k - 1: # The left tree is just one , Return node value .
return node.val
else:
node = node.left # Continue to the left tree
def _count_node_num(self, node) -> int:
""" Statistics to node Is the number of nodes of the subtree of the root node """
if not node:
return 0
self._node_num[node] = 1 + self._count_node_num(node.left) + self._count_node_num(node.right)
return self._node_num[node]
def _get_node_num(self, node) -> int:
""" To get to node Is the number of nodes of the subtree of the root node """
return self._node_num[node] if node is not None else 0
# node is not None differ not node because node May be null
class Solution:
def kthSmallest(self, root: TreeNode, k: int) -> int:
bst = Bst(root)
return bst.kth_smallest(k)
Method 3 ： Balanced binary search trees （AVL Trees ）
Balanced binary search trees ：
- The height difference between the left subtree and the right subtree of each node in the balanced binary search tree is at most 1;
- The subtree of the balanced binary search tree is also a balanced binary search tree ;
A being n The height of a balanced binary search tree of nodes is O(logn).
The time complexity of searching binary search tree in method 2 is O(H), among H Is the height of the tree ; When the tree is a balanced tree , Minimum time complexity O(logN). therefore , On the basis of recording the number of nodes of the subtree , Transform binary search tree into balanced binary search tree , And maintain its balance during insert and delete operations .
among , Transform binary search tree into balanced binary search tree , You can refer to **「1382. Solve the official problem of balancing binary search tree 」**.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class AVL:
""" Balanced binary search trees （AVL Trees ）： Duplicate values are allowed """
class Node:
""" Balanced binary search tree node """
__slots__ = ("val", "parent", "left", "right", "size", "height")
def __init__(self, val, parent=None, left=None, right=None):
self.val = val
self.parent = parent
self.left = left
self.right = right
self.height = 0 # Node height ： With node Is the height of the subtree of the root node （ Height definition ： The height of leaf nodes is 0）
self.size = 1 # Number of node elements ： With node Is the total number of nodes in the subtree of the root node
def __init__(self, vals):
self.root = self._build(vals, 0, len(vals) - 1, None) if vals else None
def _build(self, vals, l, r, parent):
""" according to vals[l:r] Construct balanced binary search tree -> Return to root node """
m = (l + r) // 2
node = self.Node(vals[m], parent=parent)
if l <= m - 1:
node.left = self._build(vals, l, m - 1, parent=node)
if m + 1 <= r:
node.right = self._build(vals, m + 1, r, parent=node)
self._recompute(node)
return node
def kth_smallest(self, k: int) -> int:
""" Returns the... In the binary search tree k Small elements """
node = self.root
while node:
left = self._get_size(node.left)
if left < k - 1:
node = node.right
k -= left + 1
elif left == k - 1:
return node.val
else:
node = node.left
def insert(self, v):
""" Insert value is v New node of """
if self.root is None:
self.root = self.Node(v)
else:
# Calculate the adding position of the new node
node = self._subtree_search(self.root, v)
is_add_left = (v <= node.val) # Whether to add a new node to node Left child node of
if node.val == v: # If the value is v The node of already exists
if node.left: # The value is v The node of has left child nodes , Is added to the rightmost part of its left subtree
node = self._subtree_last(node.left)
is_add_left = False
else: # The value is v The node of does not have a left child node , Then it is added to its left child node
is_add_left = True
# Add a new node
leaf = self.Node(v, parent=node)
if is_add_left:
node.left = leaf
else:
node.right = leaf
self._rebalance(leaf)
def delete(self, v) -> bool:
""" The deletion value is v The node of -> Returns whether the node was successfully deleted """
if self.root is None:
return False
node = self._subtree_search(self.root, v)
if node.val != v: # No node to delete was found
return False
# Handle the situation that the current node has both left and right subtrees
# If the left subtree is lower than the right subtree , Then replace the current node with the leftmost node of the right subtree , And remove the leftmost node of the right subtree
# If the right subtree is lower than the left subtree , Then replace the current node with the rightmost node of the left subtree , And remove the rightmost node of the left subtree
if node.left and node.right:
if node.left.height <= node.right.height:
replacement = self._subtree_first(node.right)
else:
replacement = self._subtree_last(node.left)
node.val = replacement.val
node = replacement
parent = node.parent
self._delete(node)
self._rebalance(parent)
return True
def _delete(self, node):
""" Delete node p And replace it with its child nodes , node p At most, there can only be 1 Child nodes """
if node.left and node.right:
raise ValueError('node has two children')
child = node.left if node.left else node.right
if child is not None:
child.parent = node.parent
if node is self.root:
self.root = child
else:
parent = node.parent
if node is parent.left:
parent.left = child
else:
parent.right = child
node.parent = node
def _subtree_search(self, node, v):
""" In order to node The search value in the subtree of the root node is v The node of , If there is no value for v The node of , The return value is v The parent node of the location where the node of should be """
if node.val < v and node.right is not None:
return self._subtree_search(node.right, v)
elif node.val > v and node.left is not None:
return self._subtree_search(node.left, v)
else:
return node
def _recompute(self, node):
""" Recalculate node Height of nodes and number of elements """
node.height = 1 + max(self._get_height(node.left), self._get_height(node.right))
node.size = 1 + self._get_size(node.left) + self._get_size(node.right)
def _rebalance(self, node):
""" from node Node start （ contain node node ） Rebalance the binary tree up one by one , And update the node height and the number of elements """
while node is not None:
old_height, old_size = node.height, node.size
if not self._is_balanced(node):
node = self._restructure(self._tall_grandchild(node))
self._recompute(node.left)
self._recompute(node.right)
self._recompute(node)
if node.height == old_height and node.size == old_size:
node = None # If the node height and the number of elements have not changed, there is no need to continue to adjust upward
else:
node = node.parent
def _is_balanced(self, node):
""" Judge node Whether the nodes are balanced """
return abs(self._get_height(node.left) - self._get_height(node.right)) <= 1
def _tall_child(self, node):
""" obtain node Subtree with higher node """
if self._get_height(node.left) > self._get_height(node.right):
return node.left
else:
return node.right
def _tall_grandchild(self, node):
""" obtain node The higher subtree in the subtree with higher nodes """
child = self._tall_child(node)
return self._tall_child(child)
@staticmethod
def _relink(parent, child, is_left):
""" Reconnect parent and child nodes （ Child nodes are allowed to be empty ）"""
if is_left:
parent.left = child
else:
parent.right = child
if child is not None:
child.parent = parent
def _rotate(self, node):
""" Rotation operation """
parent = node.parent
grandparent = parent.parent
if grandparent is None:
self.root = node
node.parent = None
else:
self._relink(grandparent, node, parent == grandparent.left)
if node == parent.left:
self._relink(parent, node.right, True)
self._relink(node, parent, False)
else:
self._relink(parent, node.left, False)
self._relink(node, parent, True)
def _restructure(self, node):
"""trinode operation """
parent = node.parent
grandparent = parent.parent
if (node == parent.right) == (parent == grandparent.right): # Handle situations that require a rotation
self._rotate(parent)
return parent
else: # Handle situations that require two rotations ： The first 1 One rotation is needed after one rotation
self._rotate(node)
self._rotate(node)
return node
@staticmethod
def _subtree_first(node):
""" Return to node Is the th of the subtree of the root node 1 Elements """
while node.left is not None:
node = node.left
return node
@staticmethod
def _subtree_last(node):
""" Return to node Is the last of the subtree of the root node 1 Elements """
while node.right is not None:
node = node.right
return node
@staticmethod
def _get_height(node) -> int:
""" To get to node Is the height of the subtree of the root node """
return node.height if node is not None else 0
@staticmethod
def _get_size(node) -> int:
""" To get to node Is the number of nodes of the subtree of the root node """
return node.size if node is not None else 0
class Solution:
def kthSmallest(self, root: TreeNode, k: int) -> int:
def inorder(node):
if node.left:
inorder(node.left)
inorder_lst.append(node.val)
if node.right:
inorder(node.right)
# Middle order traversal generates a list of values
inorder_lst = []
inorder(root)
# Construct balanced binary search tree
avl = AVL(inorder_lst)
# simulation 1000 Insert and delete operations
random_nums = [random.randint(0, 10001) for _ in range(1000)]
for num in random_nums:
avl.insert(num)
random.shuffle(random_nums) # List disorder
for num in random_nums:
avl.delete(num)
return avl.kth_smallest(k)
559. N The maximum depth of the fork tree
Leetcode
Same as 104. The maximum depth of a binary tree
class Solution:
def maxDepth(self, root: 'Node') -> int:
res = 0
if not root:return 0
q = [root]
while q:
q = [child for node in q for child in node.children]
res += 1
return res
# return max((self.maxDepth(child) for child in root.children), default=0) + 1 if root else 0
563. The slope of the binary tree
class Solution:
def __init__(self):
self.ans = 0
def findTilt(self, root: TreeNode) -> int:
# return node The sum of subtrees , Accumulate the slope at the same time .
# You can use member variables , It can also be used. nonlocal.
def dfs(root):
if not root: return 0
sumLeft = dfs(root.left)
sumRight = dfs(root.right)
self.ans += abs(sumLeft - sumRight)
return sumLeft + sumRight + root.val
dfs(root)
return self.ans
671. The second smallest node in a binary tree
Method 1 ： Depth-first search
The value of the root node is the first minimum . If the second smallest value does not exist , The output -1, Set initial value ans = -1.
Suppose the current node is node, If node.val > root.val, also ans = -1 （ for the first time ） perhaps node.val < ans, So update ans.
Besides , If node.val > ans, Then the values of all child nodes of the current node are >= ans, There is no need to traverse the subtree .
Finally, after traversing the complete binary tree , return ans.
class Solution:
def findSecondMinimumValue(self, root: TreeNode) -> int:
ans = -1
def dfs(node: TreeNode) -> None:
nonlocal ans
if not node or node.val >= ans > -1: return
if node.val > root.val: # ans First update or smaller
ans = node.val
dfs(node.left)
dfs(node.right)
dfs(root)
return ans
Implement... With collections , Judgment is simpler .
class Solution(object):
def findSecondMinimumValue(self, root: TreeNode)--> int:
res = set()
def dfs(node):
if not node: return
if node.val != root.val:
res.add(node.val)
return
dfs(node.left)
dfs(node.right)
dfs(root)
res = sorted(res)
return -1 if not res else res[0]
Method 2 ：
The idea is simple , If the node is not empty , Save its value , The left and right nodes are not empty , Join the queue .
class Solution:
def findSecondMinimumValue(self, root: TreeNode) -> int:
s = set()
queue = [root]
while queue:
node = queue.pop()
if len(s)>1 and node.val >= sorted(s)[1]:continue # Optimize ： Remove the unqualified ones
s.add(node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return -1 if len(s) < 2 else sorted(s)[1]
Further optimization
class Solution:
def findSecondMinimumValue(self, root: TreeNode) -> int:
ans = -1
queue = [root]
while queue:
node = queue.pop()
# if len(s)>1 and node.val >= sorted(s)[1]:continue
if node.val >= ans > -1: continue
if node.val > root.val: # ans First update or smaller
ans = node.val
continue
# if node.val > root.val:
# # ans Has not been reassigned （-1）, The direct assignment is node.val Assigned , Minimum value
# ans = node.val if ans == -1 else min(ans, node.val)
# continue
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return ans
Traversing the binary tree
A binary tree consists of root nodes (val)、 The left subtree (left) And right subtree (right) Three parts , If specified M、L、R Represent the val、left、right, Then the traversal way of binary tree is 6 Kind of ：
MLR - MRL - LMR - LRM - RDL - RLD
Because first traverse left And traverse first right There is no essential difference in algorithm design , therefore , Just look at the most widely used 3 Kind of （ Left right after the first , It is more in line with our current writing order , It's good for understanding ） that will do （dfs: Deep optimization ）, Of course, in addition to these methods , Traversal method and sequence traversal method （bfs: breadth-first ）：
- MLR The former sequence traversal : val -> left -> right
- LMR In the sequence traversal ：left -> val -> right
- LRM After the sequence traversal ：left -> right -> val
The above traversal method , Can be achieved by the following methods ：
- Recursive ： recursive
- Iteration : iteration
- Morris : And the method derived to solve the problem of high spatial complexity in the above implementation scheme （ Morris Traverse ）
By recursion （ front ） -> iteration （ in ）-> Morris （ in ） In order to achieve
Preamble recursion val -> left -> right
class Solution:
def findSecondMinimumValue(self, root: TreeNode) -> int:
''' According to the meaning ： The root of a node is the minimum of all its child nodes Therefore, the root node is the minimum value in the binary tree '''
self.minValue = root.val
self.res = -1
# dfs -> preorder
self.preorder(root)
# Returns the result value
return self.res
''' dfs -> inorder @param node '''
def preorder(self, node: TreeNode) -> int:
# When the node is empty , No processing required
# When res Assigned , And the current node val Greater than res when , Just go back
if not node or node.val >= self.res > -1: return
# The current value is not equal to the minimum value , And more than before res smaller , to update res value
if node.val > self.minValue: self.res = node.val
# recursive left
self.preorder(node.left)
# recursive right
self.preorder(node.right)
Medium order iteration left -> val -> right
This method is related to recursion in time , There is not much advantage in space , But it solves the risk of stack overflow if the recursion depth is too high .
class Stack(object):
""" Stack """
def __init__(self): self.items = []
def isEmpty(self): return self.items == []
def push(self, item): self.items.append(item)
def pop(self): return self.items.pop()
class Solution:
def findSecondMinimumValue(self, root: TreeNode) -> int:
res, minValue = -1, root.val
help = Stack()
help.push(root) # First root Pressing stack
# In the sequence traversal , First traverse left, Define the current node as root.left
cur = root.left
# Stack pressing is performed only when the current node is not empty or the stack is not empty
while cur or not help.isEmpty():
# cur Not empty stack
while cur:
help.push(cur)
cur = cur.left
''' root < left < left ... None > left ... < right < left ... Every round After pressing the stack ,cur The current node is empty Take the top node out of the stack '''
cur = help.pop()
if cur.val > minValue:
# res Has not been reassigned （-1）, The direct assignment is cur.val Assigned , Minimum value
res = cur.val if res == -1 else min(res, cur.val)
# Take the top node out of the stack to cur, If cur.right Not empty for the next round of stack , If it is empty, continue to stack .
cur = cur.right
return res
Middle preface Morris
Morris Traversal is different from the above two methods in , There is no need for recursion or temporary stack space to assist in completing the middle order traversal , Spatial complexity ： Constant level , O(1).
But in order to solve the problem from child Trees To parent Trees , You need to temporarily modify the structure of the tree , In other words, it will lose the data structure advantage brought by the tree itself , Just to complete the traversal , The defects brought about , But don't worry , Restore the pointer after use
In order to better understand the principle, we need the current cur and temporary predecessor 2 A pointer to the , The specific steps are as follows ：
If the left subtree node is empty , Set the current node val Add to result set res in （ there res It's different from the code , there res To better understand
Morris The process ）,cur Point to its right subtree right node （cur = cur.right）If the left subtree is not empty , Traverse the rightmost side of the left subtree right Child node (predecessor), In the process of searching, the following will appear 2 One scenario ：
predecessor.right It's empty time , take right Pointer to cur node , cur Point to its left subtree node （cur = cur.leftcur=cur.left）
predecessor.right Isn't empty , Indicates that the original leaf node connection already exists （ Has traversed cur.left）
- take predecessor.right = nullpredecessor.right=null
- cur node val Add to result set res in res.add(cur.val)res.add(cur.val)
- cur Point to Its right node (cur = cur.rightcur=cur.right)
Repeat above 2 Step until cur Node is empty
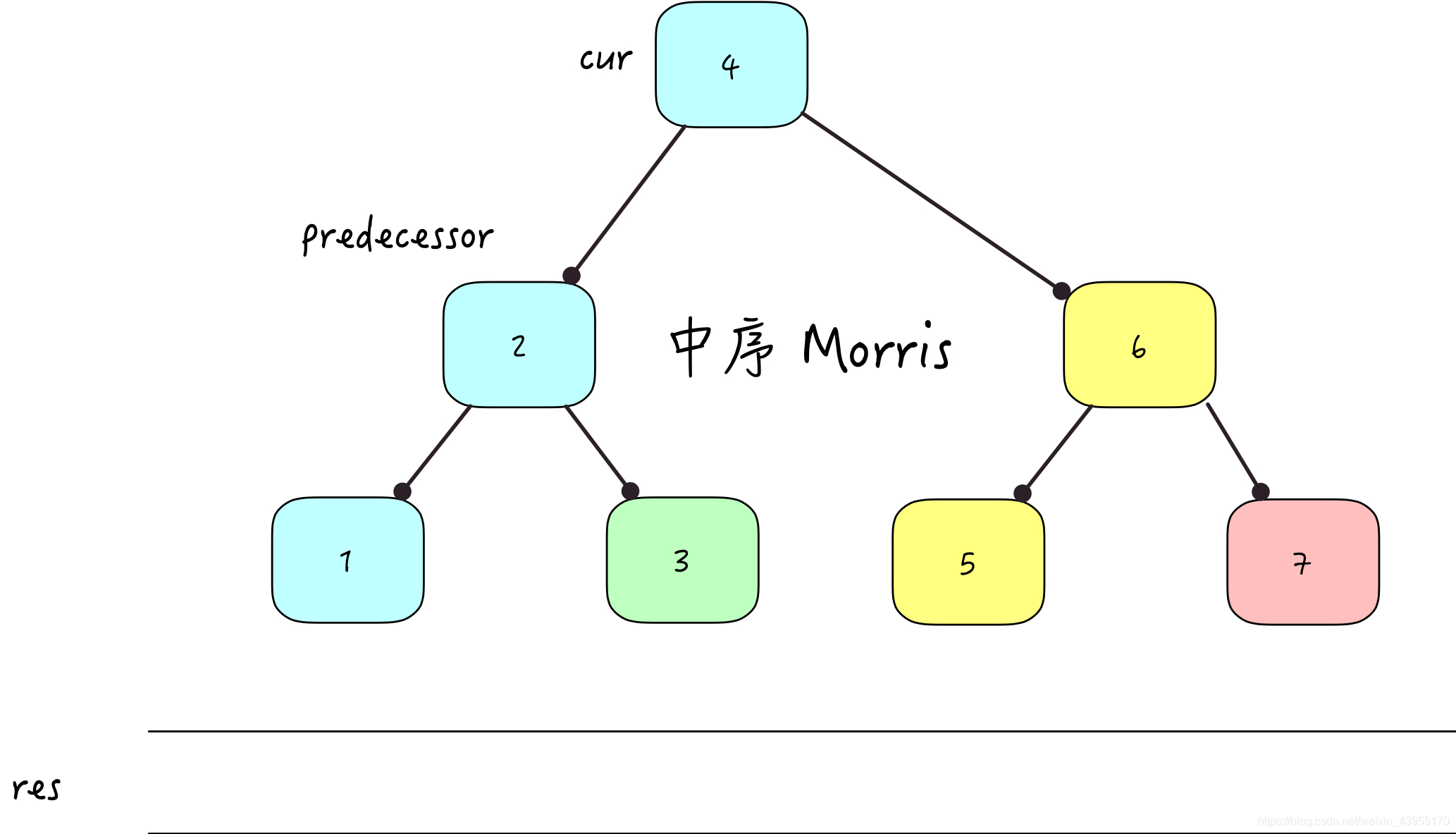
The above process is for better understanding Morris Ergodic process
This question ： According to the above res Result set , Find out the ratio root.val The second small value of large is enough , See the code comments for the specific process
class Solution:
def findSecondMinimumValue(self, root: TreeNode) -> int:
res, minValue = -1, root.val
cur = root
while cur:
# cur The left tree is empty , Put it val Judge , Compliance res The update logic of
# If the conditions are met, the current node val Update to res, , `cur` Point to its right subtree `right` node （cur = cur.right）
if not cur.left:
if cur.val > minValue:
res = cur.val if res == -1 else min(res, cur.val)
cur = cur.right
else:
# If the left subtree is not empty , look for predecessor node
predecessor = cur.left
while predecessor.right and predecessor.right != cur:
predecessor = predecessor.right
# The following corresponds to 2 Kinds of scenes
# predecessor.right It's empty
if not predecessor.right:
# take predecessor.right And cur Building links
predecessor.right = cur
# The current node points to its left Trees
cur = cur.left
else:
if cur.val > minValue:
res = cur.val if res == -1 else min(res, cur.val)
predecessor.right = None
cur = cur.right
return res
700. Search in binary search tree
class Solution:
def searchBST(self, root: TreeNode, val: int) -> TreeNode:
## Method 1 ：for
cur = root
while cur:
if cur.val == val: return cur
cur = cur.left if cur.val > val else cur.right
return None
## Method 2 ： recursive
if not root: return None
if root.val == val: return root
return self.searchBST(root.left if root.val > val else root.right, val)
863. All distances in a binary tree are K The node of
Method 1 ： Depth-first search + Hashtable
If the target As the root node of the tree , from target set out , Use depth first search with target A distance of k All of the nodes .
The binary tree does not record the parent node , From the root root set out , Use depth first search to traverse the whole tree , At the same time, a hash table is used to record the parent node of each node . The node value is unique , You can use the node value as the key of the hash table .
And then from target set out , Use depth first search to traverse the whole tree , Search left 、 Right and parent nodes .
Besides , In order to avoid repeated access to nodes during depth first search , Additional incoming source nodes frm.
class Solution:
def distanceK(self, root: TreeNode, target: TreeNode, k: int) -> List[int]:
# The values of all nodes correspond to the parent node pre = {node.val:preNode}
def findPre(node):
# if node.left:
# pre[node.left.val] = node
# findPre(node.left)
# if node.right:
# pre[node.right.val] = node
# findPre(node.right)
for n in [node.left,node.right]:
if n:
pre[n.val] = node
findPre(n)
def findAns(node, frm, depth, k):
if not node: return
if depth == k:
ans.append(node.val)
return
# if node.left != frm:
# findAns(node.left, node, depth + 1, k)
# if node.right != frm:
# findAns(node.right, node, depth + 1, k)
# if pre.get(node.val) != frm:
# findAns(pre.get(node.val), node, depth + 1, k)
# pre.get(node.val) Parent node
for n in [node.left, node.right, pre.get(node.val)]:
if n != frm:
findAns(n, node, depth + 1, k)
pre = {
} # key The value of the node ：value Corresponding parent node
ans = []
# from root set out DFS, Record the parent node of each node through the value of the node
findPre(root)
# from target set out DFS, Find all depth k The node of
findAns(target, None, 0, k)
return ans
Method 2 ：
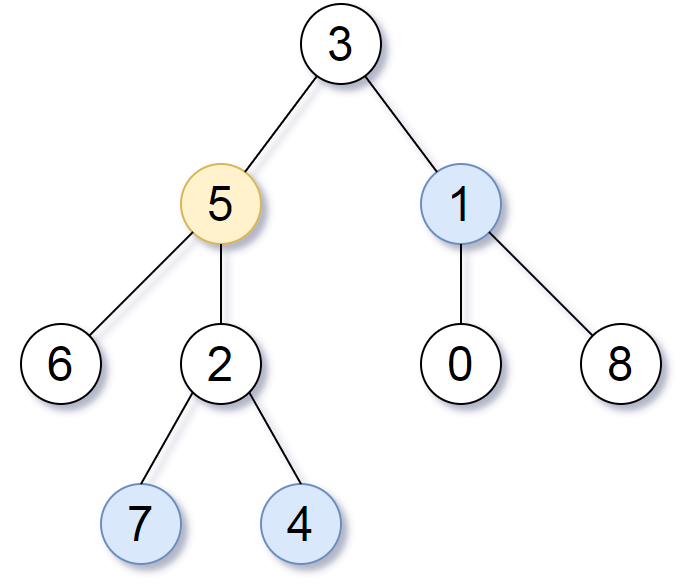
Ideas There are two situations ：
1、 Traverse all child nodes of any node findNext()
Such as ：5 => [6, 2, 7, 4] 7, 4 Match the answer
3 => [1, 0, 8] 1 Match the answer
2、 Traverse 5 All parent nodes , Just mark target Parent node of . That is to say target To root The path of .findPre()
When traversing parent nodes , Use it 1 Method traverses another branch .
Such as ：5 => 3
class Solution:
def distanceK(self, root: TreeNode, target: TreeNode, k: int) -> List[int]:
# ⑵ Recursive traversal node Child nodes of
def findNext(node, depth):
if not node: return
if depth == k:
res.append(node.val)
return
for n in [node.left, node.right]:
if n:
findNext(n, depth + 1)
# ⑶ Recursive traversal node Parent node , Process another branch at the same time , You need to mark the parent node first .
def findPre(node, depth):
# pre.get(node.val) Parent node p
p = pre.get(node.val)
if not p: return # Only root.parents = None
if depth + 1 == k:
res.append(p.val)
return
# use findNext() Search for another branch of the parent node
for x in [p.left, p.right]:
if x != node: # Get another branch node、x yes p Left and right child nodes of .
findNext(x, depth + 2)
# Recursive traversal Parent node
findPre(p, depth + 1)
res = [] # Qualified node value
pre = {
} # key Node values : value node target To root route
# ⑴ Mark only k The parent node is ok , There are many actual marks .
# You can also use recursive methods , This is used here. list.
help = [root]
pre[root] = None
while help:
node = help.pop()
for cur in [node.left, node.right]:
if cur:
pre[cur.val] = node
help.append(cur)
if cur == target:break # If you find target End
findPre(target, 0)
findNext(target, 0)
return res
1104. Binary trees find their way
Method 1 ：
Left to right binary tree , The parent node is the child node // 2;
- The first i Yes 2 i-1 Nodes , The node label is 2 i-1 to 2 i - 1;
- For the label x The node of , When x > 1 when , The label of its parent node is x // 2 .
Press one dragon , The parent node is the child node symmetric node // 2.
- Every line The sum of the labels of nodes and symmetric nodes is equal , Such as ：15 ~ 8 node 14 The symmetric node of is 15 + 8 - 14 = 9
class Solution:
def pathInZigZagTree(self, label: int) -> List[int]:
row = int(math.log(label,2)) + 1
ans = [0] * row
for i in range(row,0,-1):
ans[i-1] = label
label = (pow(2,i) - 1 - label + pow(2,i-1)) // 2
return ans
Binary tree path
Depth-first search (DFS) And breadth first search (BFS)
On the left is BFS, Search by layer ; On the right of the picture is DFS, Go all the way first , And then go back and search .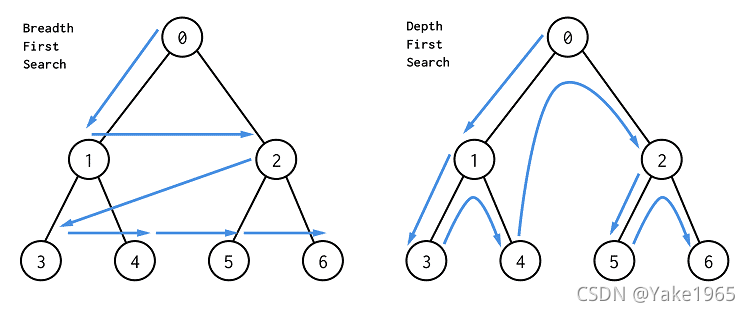
112. The sum of the paths
Leetcode
The sum of values on the path from root node to leaf node ： Judge on the leaf node .
Method 1 ： recursive DFS
class Solution:
def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
if not root:return False
if not root.left and not root.right: # leaf node
return root.val == targetSum
# The problem is transformed into left-right subtree recursion
return self.hasPathSum(root.right, targetSum - root.val) or self.hasPathSum(root.left, targetSum - root.val)
Method 2 ： Breadth first search BFS
class Solution:
def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
if not root: return False
q = deque([(root, targetSum)]) # Carry values through tuples
while q:
cur, tem = q.popleft()
tem -= cur.val
if not cur.left and not cur.right: # leaf node
if tem == 0: return True
continue
cur.left and q.append((cur.left, tem))
cur.right and q.append((cur.right, tem))
return False
113. The sum of the paths II
Method 1 ：DFS
cclass Solution:
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
def dfs(cur, tem):
# If path Pass in as a parameter , This is used here path = path + cur.val, You don't have to copy And backtracking .
path.append(cur.val)
tem -= cur.val
if not (cur.left or cur.right or tem):
res.append(path[:]) # copy
cur.left and dfs(cur.left, tem)
cur.right and dfs(cur.right, tem)
path.pop() # to flash back
if not root:return []
res , path = [], []
dfs(root, targetSum)
return res
Method 2 ：BFS
class Solution:
def pathSum(self, root: TreeNode, sum: int) -> List[List[int]]:
class Solution:
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
if not root: return []
res = []
q = deque([(root, [], targetSum)]) # node , route , Path and
while q:
cur, path, tem = q.popleft()
# path += [cur.val]
# path.append(cur.val) # list +=,append The object remains the same ！！！
path = path + [cur.val] # The object has changed
tem -= cur.val
# If it's a leaf node , Simultaneous sum is zero .
if not cur.left and not cur.right and not tem:
res.append(path) # Save the path
cur.left and q.append((cur.left, path, tem))
cur.right and q.append((cur.right, path, tem))
return res
257. All paths of binary tree
DFS
One 、 Empty node processing
1、 Recursive hollow node returns
class Solution:
def binaryTreePaths(self, root: TreeNode) -> List[str]:
def dfs(node, path):
if not node: return # Empty node return
path += str(node.val)
if not (node.left or node.right): # leaf node
res.append(path)
return
dfs(node.left, path + '->')
dfs(node.right, path + '->')
res = []
dfs(root, '')
return res
2、 Judge the empty node , There is no empty node in recursion
class Solution:
def binaryTreePaths(self, root: TreeNode) -> List[str]:
def dfs(node, path):
path += str(node.val)
if not (node.left or node.right): # leaf node
res.append(path)
node.left and dfs(node.left, path + '->') # Judge the empty node
node.right and dfs(node.right, path + '->')
res = []
dfs(root, '')
return res
Two 、 Path global variables and parameters
Global variables need to be copied and traced , When the parameter is an immutable object, you do not need , Parameters are different , Above . The parameter is the list , Use path = path + [root.val] Additive elements , in fact path Has changed. .
1、path Defined as list
class Solution:
def binaryTreePaths(self, root: TreeNode) -> List[str]:
def dfs(node):
path.append(node.val)
if not (node.left or node.right): # leaf node
res.append(path[:]) # copy
node.left and dfs(node.left)
node.right and dfs(node.right)
path.pop() # to flash back
path = []
res = []
dfs(root)
return ['->'.join(map(str,x)) for x in res]
2、path Defined as str
class Solution:
def binaryTreePaths(self, root: TreeNode) -> List[str]:
def dfs(node):
nonlocal path
path += str(node.val) if node == root else '->' + str(node.val)
if not (node.left or node.right): # leaf node
res.append(path)
node.left and dfs(node.left)
node.right and dfs(node.right)
path = path.rsplit('->', 1)[0] # to flash back
path = ''
res = []
dfs(root)
return res
BFS
class Solution:
def binaryTreePaths(self, root: TreeNode) -> List[str]:
q = deque([(root, str(root.val))]) # Carry path tuples
res = []
while q:
cur, path = q.popleft()
if not cur.left and not cur.right: # leaf node
res.append(path)
cur.left and q.append((cur.left, path + '->' + str(cur.left.val)))
cur.right and q.append((cur.right, path + '->' + str(cur.right.val)))
return res
437. The sum of the paths III
Method 1 ： Double recursion
class Solution:
def pathSum(self, root: TreeNode, targetSum: int) -> int:
def calPathSum(root, sum):
if not root: return 0
tmp = 0
sum -= root.val
if sum == 0:
tmp += 1
return tmp + calPathSum(root.left, sum) + calPathSum(root.right, sum)
if not root: return 0
return calPathSum(root, targetSum) + self.pathSum(root.left, targetSum) + self.pathSum(root.right, targetSum)
Method 2 ：
class Solution:
def pathSum(self, root: TreeNode, targetSum: int) -> int:
def f(r, s):
if r:
s = [i + r.val for i in s] + [r.val]
return s.count(targetSum) + f(r.left, s) + f(r.right, s)
return 0
return f(root, [])
988. The smallest string starting from the leaf node
Method 1 ：DFS
class Solution:
def smallestFromLeaf(self, root: TreeNode) -> str:
def dfs(node, A):
if node:
A.append(node.val)
if not node.left and not node.right:
self.ans = min(self.ans, A[::-1])
dfs(node.left, A)
dfs(node.right, A)
A.pop()
self.ans = [27]
dfs(root, [])
return ''.join(map(lambda x:chr(x + ord('a')), self.ans))
Method 2 ：BFS
class Solution:
def smallestFromLeaf(self, root: TreeNode) -> str:
res = []
q = deque([(root, [])])
while q:
cur, path = q.popleft()
path = [cur.val] + path
if not cur.left and not cur.right:
res.append(path)
cur.left and q.append((cur.left, path))
cur.right and q.append((cur.right, path))
ans = min(res)
return ''.join(map(lambda x:chr(x + 97), ans))
class Solution:
def smallestFromLeaf(self, root: TreeNode) -> str:
res = [27]
q = deque([(root, [])])
while q:
cur, path = q.popleft()
path = [cur.val] + path
if not cur.left and not cur.right:
res = min(res, path)
cur.left and q.append((cur.left, path))
cur.right and q.append((cur.right, path))
return ''.join(map(lambda x:chr(x + 97), res))
To be sorted out …
124. The maximum path in a binary tree and
687. The longest path of the same value
543. The diameter of a binary tree
vector<vector> res;
vector<vector> pathSum(TreeNode *root, int targetSum)
{
vector path;
dfs(root, targetSum, path);
return res;
}
void dfs(TreeNode*root, int sum, vector path)
{
if (!root)
return;
sum -= root->val;
path.push_back(root->val);
if (!root->left && !root->right && sum == 0)
{
res.push_back(path);
return;
}
dfs(root->left, sum, path);
dfs(root->right, sum, path);
}
437. The sum of the paths III
Double recursion ： First call dfs Function from root Start finding the path , Call again pathsum Function to root The left and right subtrees start searching
Don't pass
class Solution:
def __init__(self):
self.count = 0
def pathSum(self, root: TreeNode, sum: int) -> int:
@lru_cache(None)
def dfs(node, sum):
sum -= root.val
# Be careful not to. return, Because it is not required to end at the leaf node , So there may be another path under one path
if sum == 0:
self.count += 1 # If a path global variable is found + 1
node.left and dfs(node.left, sum)
node.right and dfs(node.right, sum)
if not root: return 0
dfs(root, sum)
self.pathSum(root.left, sum)
self.pathSum(root.right, sum)
return self.count
- The smallest string starting from the leaf node
The soup does not change the dressing , Apply template 1
vector path;
string smallestFromLeaf(TreeNode *root)
{
dfs(root, “”);
sort(path.begin(), path.end()); // Ascending sort
return path[0];
}
void dfs(TreeNode *root, string s)
{
if (!root)
return;
s += ‘a’ + root->val;
if (!root->left && !root->right)
{
reverse(s.begin(), s.end()); // The topic requires from root node to leaf node , So reverse
path.push_back(s);
return;
}
dfs(root->left, s);
dfs(root->right, s);
}
Two 、 Not top-down
124. The maximum path in a binary tree and
/left,right They are the maximum paths of the left and right subtrees of the root node and , Be careful ： If the maximum path and <0, It means that this path and make a negative contribution to the total path and , So don't count in the total path , Set it to 0
int res = INT_MIN; // Note that the node value may be negative , So set it to the minimum
int maxPathSum(TreeNode *root)
{
maxPath(root);
return res;
}
int maxPath(TreeNode *root) // With root The longest path that is the starting point of the path
{
if (!root)
return 0;
int left = max(maxPath(root->left), 0);
int right = max(maxPath(root->right), 0);
res = max(res, left + right + root->val); // Compare the current maximum path with the larger value of the longest path of the left and right subtrees plus the root node value , Update global variables
return max(left + root->val, right + root->val); // Return the long path of the left and right subtrees plus the root node value
}
687. The longest path of the same value
int longestUnivaluePath(TreeNode *root)
{
if (!root)
return 0;
longestPath(root);
return res;
}
int longestPath(TreeNode *root)
{
if (!root)
return 0;
int left = longestPath(root->left), right = longestPath(root->right);
// If the left child node and the root node have the same value , Update left longest path ; Otherwise, the left longest path is 0
if (root->left && root->val == root->left->val)
left++;
else
left = 0;
if (root->right && root->val == root->right->val)
right++;
else
right = 0;
res = max(res, left + right);
return max(left, right);
}
543. The diameter of a binary tree
int res1 = 0;
int diameterOfBinaryTree(TreeNode *root)
{
maxPath(root);
return res1;
}
int maxPath(TreeNode *root)
{
// Here, the recursive end condition should pay special attention to ： It can't be !root( And there is no need to judge root It's empty , Because only non null will enter recursion ), Because the path length of a single node is also 0
if (!root->left && !root->right)
return 0;
int left = root->left ? maxPath(root->left) + 1 : 0; // Determine whether the left child node is empty , This updates the longest path on the left
int right = root->right ? maxPath(root->right) + 1 : 0;
res1 = max(res, left + right); // Update global variables
return max(left, right); // Return to the larger of the left and right paths
}
边栏推荐
- 位运算（Bit Operation）
- Line test - graphic reasoning - 3 - symmetric graphic class
- [network] Introduction to C language
- iNFTnews | NFT技术的广泛应用及其存在的问题
- Cause analysis and solution of too laggy page of [test interview questions]
- 软件测评中心▏自动化测试有哪些基本流程和注意事项?
- U盘拷贝东西时，报错卷错误，请运行chkdsk
- Transparent i/o model from beginning to end
- 智慧社區和智慧城市之間有什麼异同
- I wish you all the best and the year of the tiger
猜你喜欢
It's no exaggeration to say that this is the most user-friendly basic tutorial of pytest I've ever seen
Microbial health network, how to restore microbial communities
LeetCode707. Design linked list
leetcode-520. 检测大写字母-js
Innovation today ｜ five key elements for enterprises to promote innovation
【刷题记录】3. 无重复字符的最长子串
Gbu1510-asemi power supply special 15A rectifier bridge gbu1510
![Leetcode19. Delete the penultimate node of the linked list [double pointer]](/img/a9/809b93d1ffd11ba4a9074ac8e2bdee.jpg)
Leetcode19. Delete the penultimate node of the linked list [double pointer]
Introduction to redis and jedis and redis things
How to operate DTC community?
随机推荐
关于海康ipc的几个参数
Line measurement - graphic reasoning -9- line problem class
微信论坛交流小程序系统毕业设计毕设（8）毕业设计论文模板
Leetcode19. Delete the penultimate node of the linked list [double pointer]
Lecture 30 linear algebra Lecture 5 eigenvalues and eigenvectors
The author of LinkedList said he didn't use LinkedList himself
Sword finger offer 28 Symmetric binary tree
30讲 线性代数 第五讲 特征值与特征向量
开发那些事儿：Go加C.free释放内存，编译报错是什么原因？
Anta DTC | Anta transformation, building a growth flywheel that is not only FILA
Debezium series: introducing support for the final operator
./ setup. Insufficient sh permission
今日创见｜企业促进创新的5大关键要素
ArcGIS：矢量要素相同字段属性融合的两种方法
数字藏品加速出圈，MarsNFT助力多元化文旅经济！
Line test - graphic reasoning - 4 - alphabetic class
面试百问：如何测试App性能？
LeetCode142. Circular linked list II [two pointers, two methods for judging links in the linked list and finding ring points]
网络安全-beef
ArcGIS：字段赋值_属性表字段计算器（Field Calculator）依据条件为字段赋值