当前位置:网站首页>Trigonometric identity transformation formula
Trigonometric identity transformation formula
2022-07-31 14:26:00 【AoBeiChuan】
1.和角公式
- sin ( A + B ) = sin A cos B + cos A sin B \text{sin}{(A+B)}=\text{sin}A\text{cos}B+\text{cos}A\text{sin}B sin(A+B)=sinAcosB+cosAsinB
- cos ( A + B ) = cos A cos B − sin A sin B \text{cos}{(A+B)}=\text{cos}A\text{cos}B-\text{sin}A\text{sin}B cos(A+B)=cosAcosB−sinAsinB
- tan ( A + B ) = t a n A + t a n B 1 − t a n A t a n B \text{tan}(A+B)=\cfrac{tanA+tanB}{1-tanAtanB} tan(A+B)=1−tanAtanBtanA+tanB
2.差角公式
- sin ( A − B ) = sin A cos B − cos A sin B \text{sin}{(A-B)}=\text{sin}A\text{cos}B-\text{cos}A\text{sin}B sin(A−B)=sinAcosB−cosAsinB
- cos ( A − B ) = cos A cos B + sin A sin B \text{cos}{(A-B)}=\text{cos}A\text{cos}B+\text{sin}A\text{sin}B cos(A−B)=cosAcosB+sinAsinB
- tan ( A − B ) = t a n A − t a n B 1 + t a n A t a n B \text{tan}(A-B)=\cfrac{tanA-tanB}{1+tanAtanB} tan(A−B)=1+tanAtanBtanA−tanB
3.倍角公式
- sin 2 a = 2 sin a cos a \text{sin}{2a}=2\text{sin}a\text{cos}a sin2a=2sinacosa
- cos 2 a = cos 2 a − sin 2 a = 2 cos 2 a − 1 = 1 − 2 sin 2 a \text{cos}{2a}=\text{cos}^2a-\text{sin}^2a=2\text{cos}^2a-1=1-2\text{sin}^2a cos2a=cos2a−sin2a=2cos2a−1=1−2sin2a
- tan 2 a = 2 tan a 1 − tan 2 a \text{tan}{2a}=\cfrac{2\text{tan}a}{1-\text{tan}^2a} tan2a=1−tan2a2tana
4.辅助角公式
- a sin x + b cos x = ( a 2 + b 2 sin ( x + ψ ) a\text{sin}x+b\text{cos}x=\sqrt{\mathstrut {a^2+b^2}}\text{sin}(x+\psi) asinx+bcosx=(a2+b2sin(x+ψ)
其中: cos ψ = 1 ( a 2 + b 2 \text{cos}{\psi}=\cfrac{1}{\sqrt{\mathstrut {a^2+b^2}}} cosψ=(a2+b21
5.积化和差公式
- sin A cos B = 1 2 [ sin ( A + B ) + sin ( A − B ) ] \text{sin}A\text{cos}B=\cfrac{1}{2}[\text{sin}(A+B)+\text{sin}(A-B)] sinAcosB=21[sin(A+B)+sin(A−B)]
- cos A cos B = 1 2 [ cos ( A + B ) + cos ( A − B ) ] \text{cos}A\text{cos}B=\cfrac{1}{2}[\text{cos}(A+B)+\text{cos}(A-B)] cosAcosB=21[cos(A+B)+cos(A−B)]
- sin A sin B = 1 2 [ cos ( A + B ) − cos ( A − B ) ] \text{sin}A\text{sin}B=\cfrac{1}{2}[\text{cos}(A+B)-\text{cos}(A-B)] sinAsinB=21[cos(A+B)−cos(A−B)]
6.和差化积公式
- sin A + sin B = 2 sin A + B 2 cos A − B 2 \text{sin}A+\text{sin}B=2\text{sin}\cfrac{A+B}{2}\text{cos}\cfrac{A-B}{2} sinA+sinB=2sin2A+Bcos2A−B
- sin A − sin B = 2 cos A + B 2 sin A − B 2 \text{sin}A-\text{sin}B=2\text{cos}\cfrac{A+B}{2}\text{sin}\cfrac{A-B}{2} sinA−sinB=2cos2A+Bsin2A−B
- cos A + cos B = 2 cos A + B 2 cos A − B 2 \text{cos}A+\text{cos}B=2\text{cos}\cfrac{A+B}{2}\text{cos}\cfrac{A-B}{2} cosA+cosB=2cos2A+Bcos2A−B
- cos A − cos B = 2 sin A + B 2 sin A − B 2 \text{cos}A-\text{cos}B=2\text{sin}\cfrac{A+B}{2}\text{sin}\cfrac{A-B}{2} cosA−cosB=2sin2A+Bsin2A−B
边栏推荐
- OAuth2:搭建授权服务器
- redhat/openssl生成自签ca证书并使用
- 1小时直播招募令:行业大咖干货分享,企业报名开启丨量子位·视点
- ADS communicate with c #
- 海康摄像机取流RTSP地址规则说明
- element-plus虚拟表格virtual-list组件中是怎么实现清理lodash.memoize缓存的?
- The paper manual becomes 3D animation in seconds, the latest research of Wu Jiajun of Stanford University, selected for ECCV 2022
- The recently popular domestic interface artifact Apipost experience
- Miller_Rabin 米勒拉宾概率筛【模板】
- Shell script classic case: backup of files
猜你喜欢
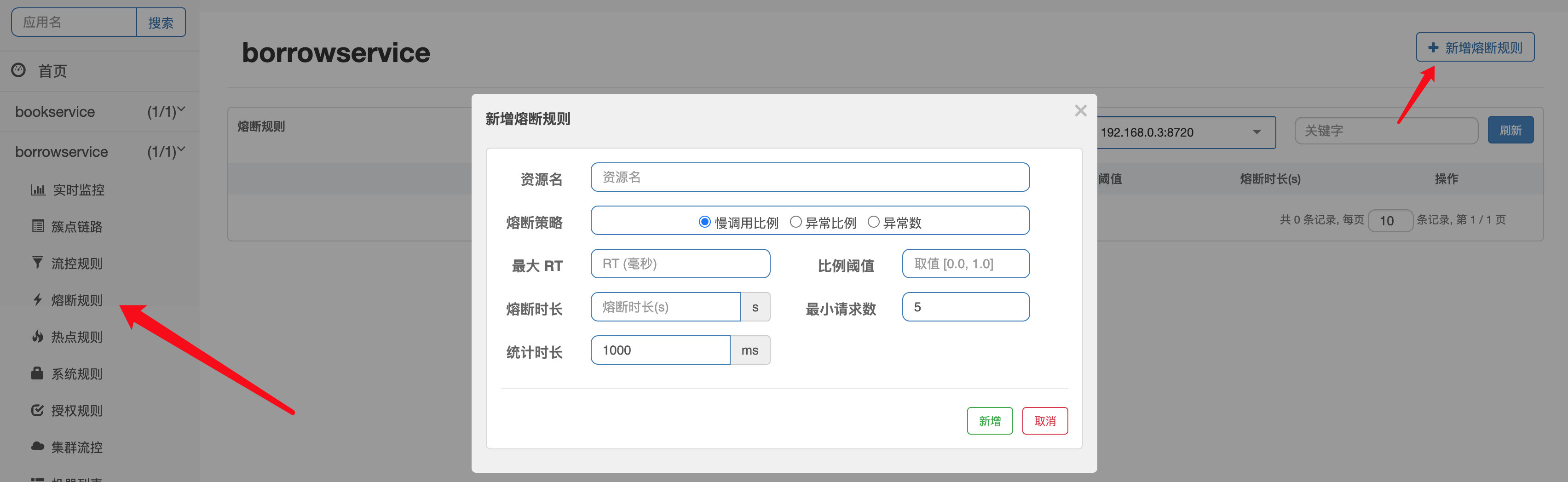
Sentinel服务熔断和降级

49.【拷贝构造函数与重载】
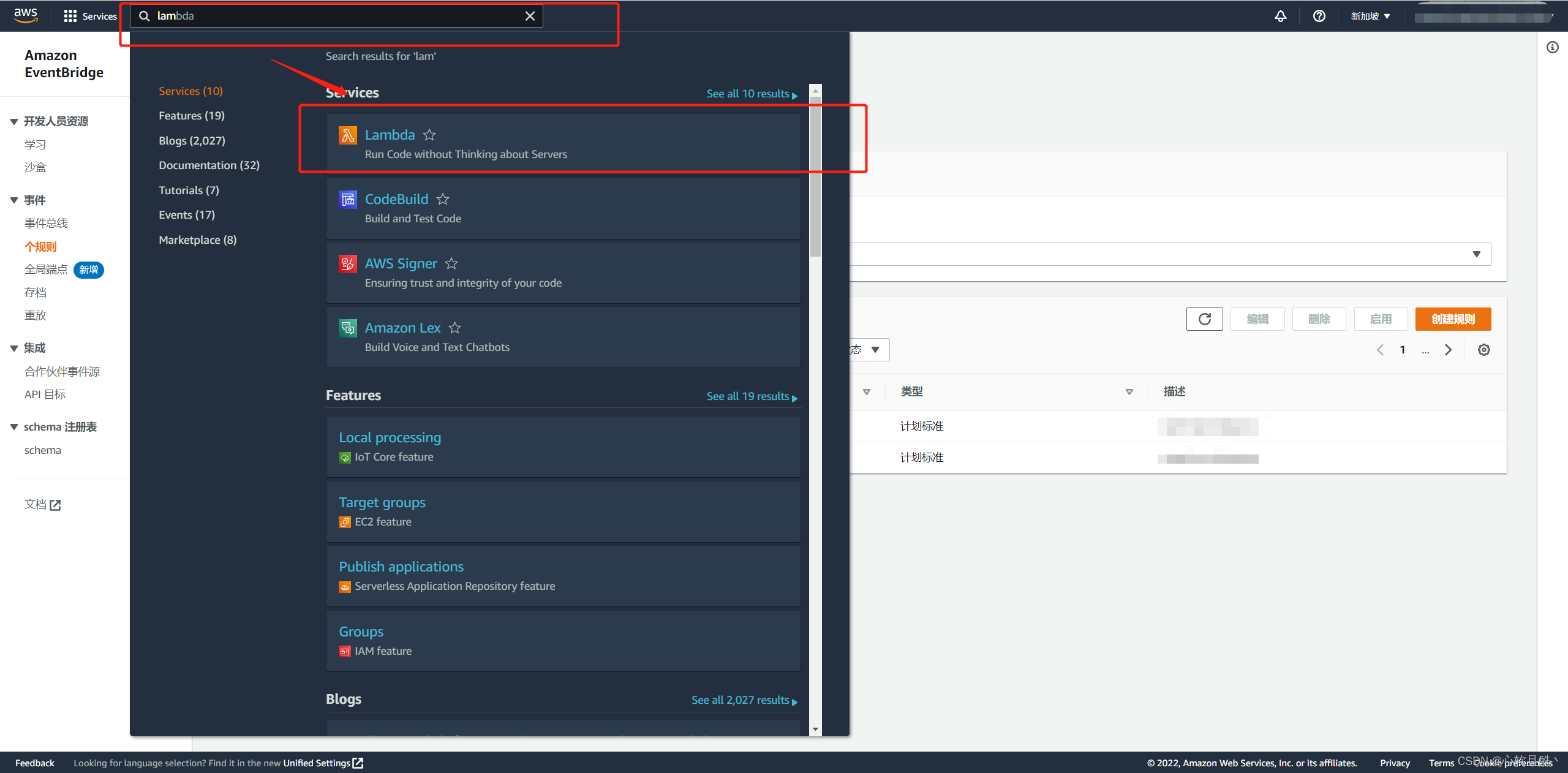
AWS implements scheduled tasks - Lambda+EventBridge

使用CompletableFuture进行异步处理业务

For enterprises in the digital age, data governance is difficult, but it should be done

OAuth2:单点登陆客户端
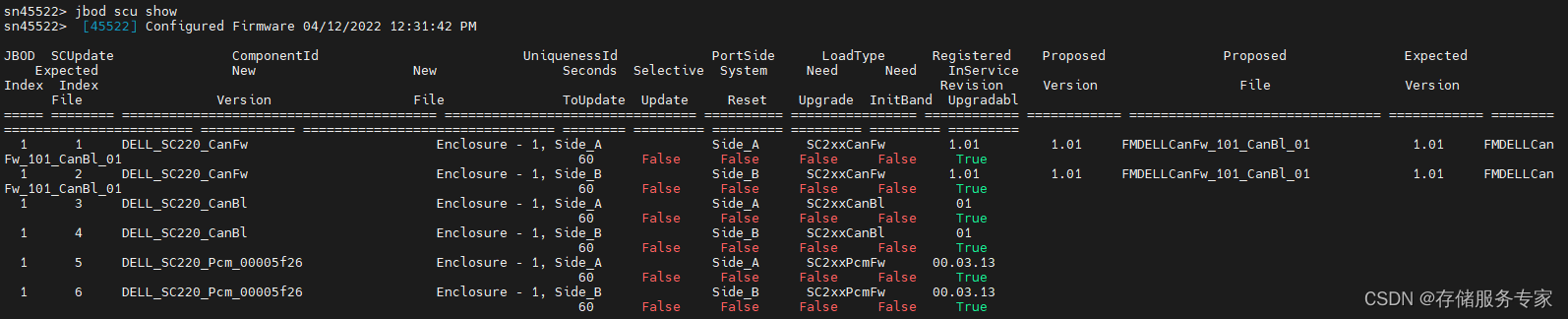
DELL SC compellent 康贝存储系统怎么抓取配置信息

最近很火的国产接口神器Apipost体验

UnityShader入门学习(二)——渲染流水线

The 232-layer 3D flash memory chip is here: the single-chip capacity is 2TB, and the transmission speed is increased by 50%
随机推荐
小试牛刀:Go 反射帮我把 Excel 转成 Struct
sentinel与nacos持久化
Nuget打包并上传教程
Node version switching management using NVM
Sentinel限流和异常处理
DeepLab Series Learning
jvm 一之 类加载器
OpenShift 4 - 用 Operator 部署 Redis 集群
For enterprises in the digital age, data governance is difficult, but it should be done
技能大赛dhcp服务训练题
LeetCode·304竞赛·6132·使数组中所有元素都等于零·模拟·哈希
IDEA connects to MySQL database and uses data
Nuget package and upload tutorial
Use of el-tooltip
The recently popular domestic interface artifact Apipost experience
多智能体协同控制研究中光学动作捕捉与UWB定位技术比较
Network cable RJ45 interface pins [easy to understand]
Small test knife: Go reflection helped me convert Excel to Struct
Resnet&API
Shell脚本经典案例:探测批量主机是否存活