当前位置:网站首页>The concept, implementation and analysis of binary search tree (BST)
The concept, implementation and analysis of binary search tree (BST)
2022-07-07 11:06:00 【Exy-】
Catalog
BST The deletion of ( important )
Binary search tree
Concept
Binary search tree is also called binary sort tree , It could be an empty tree , Or a binary tree with the following properties :
- If its left subtree is not empty , Then the values of all nodes on the left subtree are smaller than the values of the root nodes
- If its right subtree is not empty , Then the value of all nodes on the right subtree is greater than the value of the root node
- Its left and right subtrees are also binary search trees
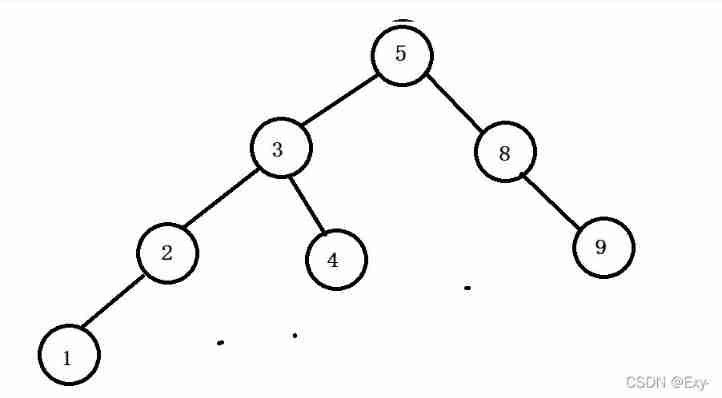
int ar[]={5,3,2,4,8,9,1};
BST Insertion of trees
- If the tree is empty, it will be inserted directly ;
- If it's not empty , Then insert according to the rules of binary search tree .
bool Insert(const K& key, const V& value)
{
if (_root == nullptr)
{
_root = new Node(key, value);
return true;
}
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key, value);
if (cur->_key > parent->_key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}BST Tree search
If the root node _root->_key== You're looking for key Return the found node
If the root node _root->_key> You're looking for key Look on its left sub tree
If the root node _root->_key< You're looking for key Look on its right subtree
If the root node does not exist , Return null pointer
Node* Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}BST The deletion of ( important )
First of all, according to the key Find nodes , No return found false;
There are three cases of deletion
1. The left subtree of the node to be deleted is empty
- The root node to delete , Let the root be equal to the right child node
- The left child node that is an ordinary node and its parent node to be deleted is parent->_left = cur->_right
- The right child node that is an ordinary node and its parent node to be deleted is parent->_right= cur->_right
2. The right subtree of the node to be deleted is empty
- The root node to delete , Let the root be equal to the left child node
- The left child node that is an ordinary node and its parent node to be deleted is parent->_left = cur->_left;
- The left child node that is an ordinary node and its parent node to be deleted is parent->_right = cur->_left;
3. The left and right child nodes of the deleted node are not empty :
We use the substitution method here
Find the largest node of the left subtree ( The most right ) Or the smallest node of the right subtree
The code is as follows :
bool Erase(const K& key)
{
//1. Looking for nodes
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
if (cur->_left == nullptr)
{
if (parent == nullptr)// The root node to delete
{
_root = cur->_right;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr)
{
if (parent == nullptr)
{
_root = cur->_left;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
}
else
{
// The substitution method deletes The largest node of the left tree ( The rightmost node ) Or the smallest node of the right tree ( Leftmost node )
Node* Parent = cur; // Be careful not to initialize null
Node* minNode = cur->_right;
while (minNode->_left)
{
Parent = minNode;
minNode = minNode->_left;
}
swap(cur->_key, minNode->_key);
// Convert to delete minNode
// because minNode As an empty node , You can delete
if (Parent->_right == minNode)
Parent->_right = minNode->_right;
else
Parent->_left = minNode->_right;
delete minNode;
}
return true;
}
}
return false;
}application
according to BST We can realize the characteristics of trees
Performance analysis


边栏推荐
- [système recommandé 01] rechub
- 【STM32】实战3.1—用STM32与TB6600驱动器驱动42步进电机(一)
- TypeScript 接口继承
- Wallhaven wallpaper desktop version
- Différences entre les contraintes monotones et anti - monotones
- Find the root of equation ax^2+bx+c=0 (C language)
- 【推荐系统 02】DeepFM、YoutubeDNN、DSSM、MMOE
- Basic introduction of yarn and job submission process
- Which securities company is the best and safest to open an account for the subscription of new shares
- Go-Redis 中间件
猜你喜欢
Find the root of equation ax^2+bx+c=0 (C language)
【pyqt】tableWidget里的cellWidget使用信号与槽机制
![[untitled]](/img/c2/d70d052b7e9587dc81c622f62f8566.jpg)
[untitled]
Applet jump to H5, configure business domain name experience tutorial

Unity script generates configurable files and loads
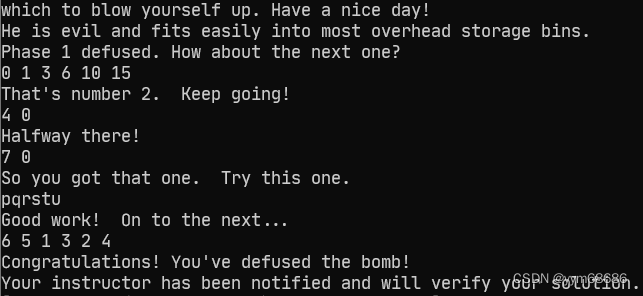
CSAPP bomb lab parsing
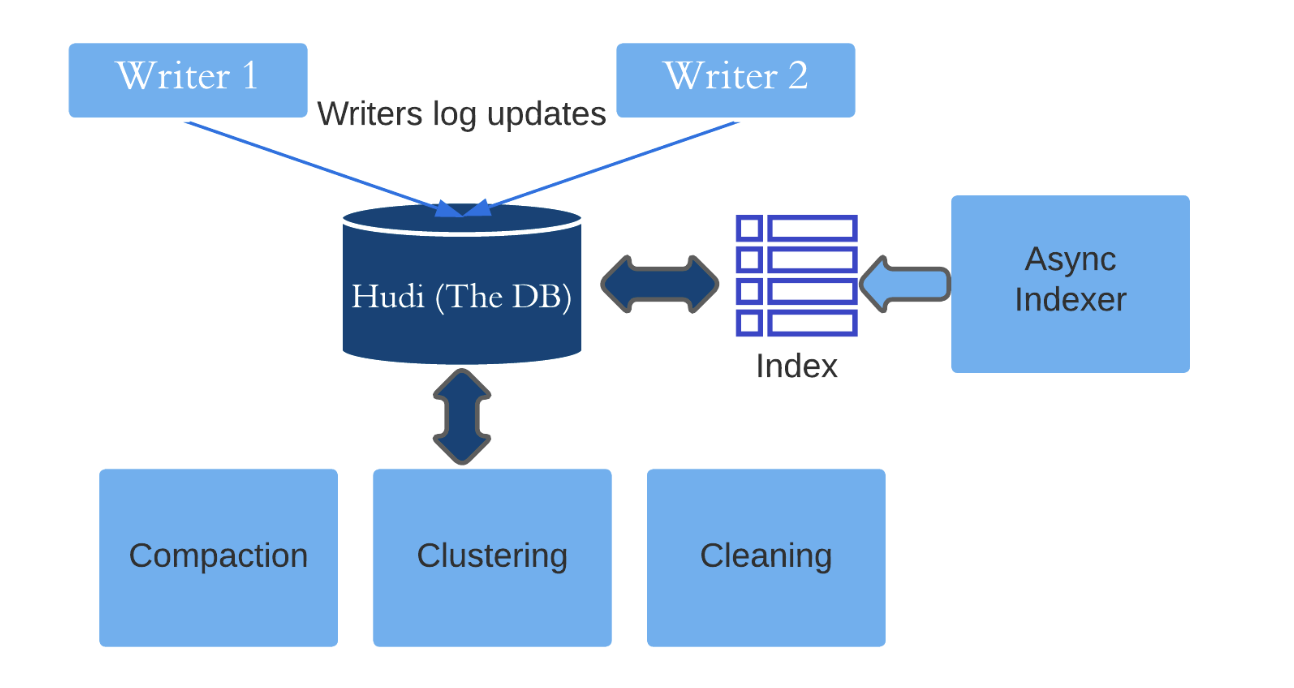
深入理解Apache Hudi异步索引机制
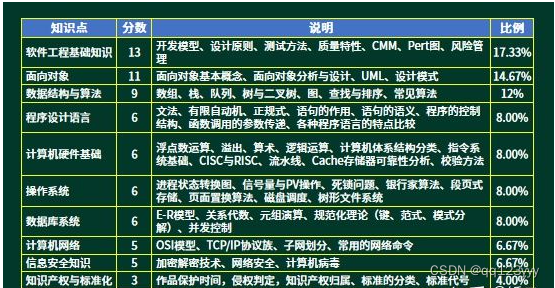
What are the contents of the intermediate soft test, the software designer test, and the test outline?
高级软考(网络规划设计师)该如何备考?
![[untitled]](/img/c7/b6abe0e13e669278aea0113ca694e0.jpg)
[untitled]
随机推荐
ADB utility commands (network package, log, tuning related)
Still cannot find RPC dispatcher table failed to connect in virtual KD
【STM32】实战3.1—用STM32与TB6600驱动器驱动42步进电机(一)
Go Slice 比较
The gun startles the dragon, and the crowd "locks" Zhou Zhi
Compile QT project script with qmake
2021 summary and 2022 outlook
2022年7月10日“五心公益”活动通知+报名入口(二维码)
[untitled]
【亲测可行】error while loading shared libraries的解决方案
July 10, 2022 "five heart public welfare" activity notice + registration entry (two-dimensional code)
seata 1.3.0 四种模式解决分布式事务(AT、TCC、SAGA、XA)
TypeScript 接口继承
【pyqt】tableWidget里的cellWidget使用信号与槽机制
Applet jump to H5, configure business domain name experience tutorial
The eighth training assignment
PHP \ newline cannot be output
Online hard core tools
【C#】WinForm运行缩放(变糊)的解决方法
Unable to open kernel device '\.\vmcidev\vmx': operation completed successfully. Reboot after installing vmware workstation? Module "devicepoweron" failed to start. Failed to start the virtual machine