当前位置:网站首页>信息学奥赛一本通 1339:【例3-4】求后序遍历 | 洛谷 P1827 [USACO3.4] 美国血统 American Heritage
信息学奥赛一本通 1339:【例3-4】求后序遍历 | 洛谷 P1827 [USACO3.4] 美国血统 American Heritage
2022-07-05 20:10:00 【君义_noip】
【题目链接】
ybt 1339:【例3-4】求后序遍历
洛谷 P1827 [USACO3.4] 美国血统 American Heritage
两题都是已知先序和中序遍历序列,求后序遍历序列
区别为:【ybt 1339】先输入先序遍历序列,再输入中序遍历序列。【洛谷 P1827】先输入中序遍历序列,再输入先序遍历序列。
【题目考点】
1. 二叉树
已知先序、中序边路序列,求后序遍历序列
【解题思路】
解法1:
假设输入的中序遍历序列为:DBAECH,先序遍历序列为ABDCEF。以该输入为例讨论问题解法。
当前要解决的问题是:已知先序、中序遍历序列,构建二叉树。
- 首先先序遍历中第一个字母为树的根结点的值(A)。
- 而后在中序遍历序列中找到根结点值(A)的位置,根结点值左边的序列(DB)是根结点的左子树的中序遍历序列。根结点值右边的序列(ECF)为根结点的右子树的中序遍历序列。
- 在先序遍历序列中根据左子树中序遍历序列的长度,找到左子树的先序遍历序列(BD),及右子树的先序遍历序列(CEF)。
- 递归调用“已知先序中序遍历序列求二叉树”的函数。现在已知根结点的左子树、右子树的先序、中序遍历序列,那么就可以构建出根结点的左子树与右子树(构建子树相对于构建以A为根结点的树,是小规模问题,递归求解大规模问题时,小规模问题的解被视为是已知的)
- 以A为根结点,接上构造好的左右子树,即完成了树的构建。
接下来对这棵树做后序遍历,即可得到树的后序遍历序列。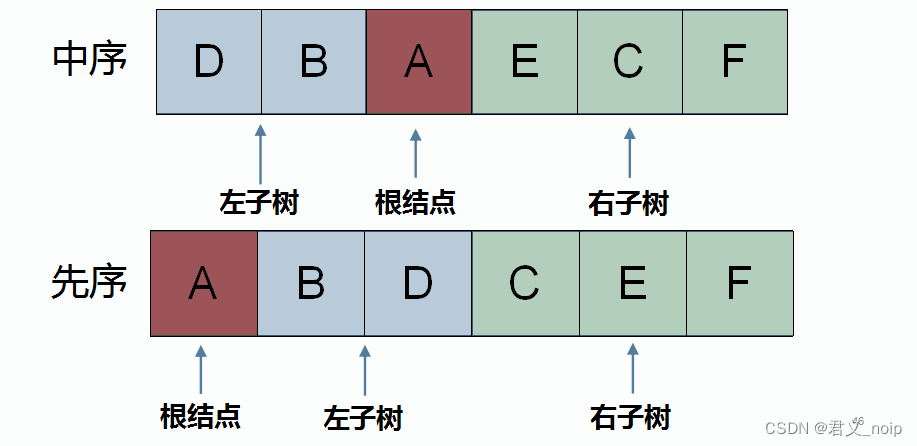
写法1:使用字符数组
输入先序遍历序列到s_pre,中序遍历序列到字符数组s_in。
函数createTree需要传入ml,mr,pl,pr,意为:由先序序列s_pre[pl]~s_pre[pr]与中序序列s_in[ml]~s_in[mr]构造一棵二叉树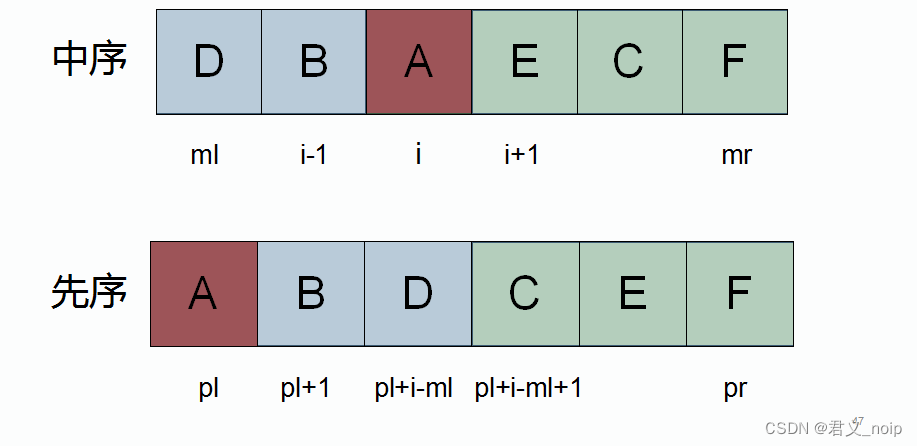
根据上述算法,先在中序序列中找到先序序列第一个字符s_pre[pl]的位置,找到位置为i。那么左子树的中序遍历序列为s_in[ml]~s_in[i-1],长度为i-ml,在先序遍历序列中,从pl+1开始取长为i-ml的序列,最后一个元素的位置为pl+i-ml,那么左子树的先序遍历序列为s_pre[pl+1]~s_pre[pl+i-ml]。类似地,可以得到右子树的中序序列为s_in[i+1]~s_in[mr],先序序列为s_pre[pl+i-ml+1]~s_pre[pr]。
使用createTree分别生成左右子树,接在新分配出来的根结点的下面,就得到了这棵树。
递归出口为:先序与中序序列的下标范围一定有pl<=pr且ml<=mr,如果不满足这一条件,序列范围无意义,应该返回。
写法2:使用string类
思路与上述方法类似,不再赘述。
使用string类,可以使用substr成员函数来取子串。每次传入函数的先序、中序序列都是string类对象。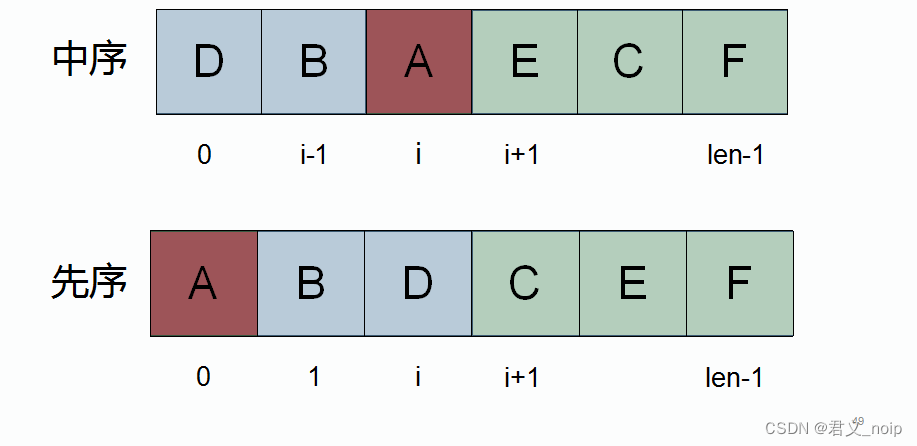
【题解代码】:ybt 1339:【例3-4】求后序遍历
写法1:使用字符数组
#include <bits/stdc++.h>
using namespace std;
#define N 1000
struct Node
{
char val;
int left, right;
};
Node node[N];
int p = 1;
char s_pre[105], s_in[105];//s_pre:先序遍历序列 s_in:中序遍历序列
//由先序序列s_pre[pl]~s_pre[pr]与中序序列s_in[ml]~s_in[mr]构造一棵二叉树,返回根结点
int createTree(int pl, int pr, int ml, int mr)
{
if(pl > pr || ml > mr)
return 0;
int np = p++, i;
node[np].val = s_pre[pl];
for(i = ml; i <= mr; ++i)
{
if(s_in[i] == s_pre[pl])
break;
}
node[np].left = createTree(pl + 1, pl + i - ml, ml, i - 1);
node[np].right = createTree(pl + i - ml + 1, pr, i + 1, mr);
return np;
}
void postOrder(int root)
{
if(root != 0)
{
postOrder(node[root].left);
postOrder(node[root].right);
cout << node[root].val;
}
}
int main()
{
cin >> s_pre >> s_in;
int root = createTree(0, strlen(s_pre) - 1, 0, strlen(s_in) - 1);
postOrder(root);
return 0;
}
写法2:使用string类
#include <bits/stdc++.h>
using namespace std;
#define N 1000
struct Node
{
char val;
int left, right;
};
Node node[N];
int p = 1;
string s_pre, s_in;
int createTree(string sp, string si)//用先序序列sp与中序序列si构建二叉树,返回树根
{
int np = p++, i;
node[np].val = sp[0];
for(i = 0; i < si.length(); ++i)
{
if(sp[0] == si[i])
break;
}
int len_l = i, len_r = si.length() - 1 - i;//左右子树序列长度
if(len_l > 0)//序列长度大于0,才可以建立一棵树
node[np].left = createTree(sp.substr(1, len_l), si.substr(0, len_l));
if(len_r > 0)
node[np].right = createTree(sp.substr(i+1, len_r), si.substr(i+1, len_r));
return np;
}
void postOrder(int root)
{
if(root != 0)
{
postOrder(node[root].left);
postOrder(node[root].right);
cout << node[root].val;
}
}
int main()
{
cin >> s_pre >> s_in;
int root = createTree(s_pre, s_in);
postOrder(root);
return 0;
}
【题解代码】:洛谷 P1827 [USACO3.4] 美国血统 American Heritage
写法1:使用字符数组
#include <bits/stdc++.h>
using namespace std;
#define N 1000
struct Node
{
char val;
int left, right;
};
Node node[N];
int p = 1;
char s_pre[105], s_in[105];//s_pre:先序遍历序列 s_in:中序遍历序列
//由先序序列s_pre[pl]~s_pre[pr]与中序序列s_in[ml]~s_in[mr]构造一棵二叉树,返回根结点
int createTree(int pl, int pr, int ml, int mr)
{
if(pl > pr || ml > mr)
return 0;
int np = p++, i;
node[np].val = s_pre[pl];
for(i = ml; i <= mr; ++i)
{
if(s_in[i] == s_pre[pl])
break;
}
node[np].left = createTree(pl + 1, pl + i - ml, ml, i - 1);
node[np].right = createTree(pl + i - ml + 1, pr, i + 1, mr);
return np;
}
void postOrder(int root)
{
if(root != 0)
{
postOrder(node[root].left);
postOrder(node[root].right);
cout << node[root].val;
}
}
int main()
{
cin >> s_in >> s_pre;
int root = createTree(0, strlen(s_pre) - 1, 0, strlen(s_in) - 1);
postOrder(root);
return 0;
}
写法2:使用string类
#include <bits/stdc++.h>
using namespace std;
#define N 1000
struct Node
{
char val;
int left, right;
};
Node node[N];
int p = 1;
string s_pre, s_in;
int createTree(string sp, string si)//用先序序列sp与中序序列si构建二叉树,返回树根
{
int np = p++, i;
node[np].val = sp[0];
for(i = 0; i < si.length(); ++i)
{
if(sp[0] == si[i])
break;
}
int len_l = i, len_r = si.length() - 1 - i;//左右子树序列长度
if(len_l > 0)//序列长度大于0,才可以建立一棵树
node[np].left = createTree(sp.substr(1, len_l), si.substr(0, len_l));
if(len_r > 0)
node[np].right = createTree(sp.substr(i+1, len_r), si.substr(i+1, len_r));
return np;
}
void postOrder(int root)
{
if(root != 0)
{
postOrder(node[root].left);
postOrder(node[root].right);
cout << node[root].val;
}
}
int main()
{
cin >> s_in >> s_pre;
int root = createTree(s_pre, s_in);
postOrder(root);
return 0;
}
边栏推荐
- Securerandom things | true and false random numbers
- The difference between ID selector and class selector
- B站UP搭建世界首个纯红石神经网络、基于深度学习动作识别的色情检测、陈天奇《机器学编译MLC》课程进展、AI前沿论文 | ShowMeAI资讯日报 #07.05
- Flume series: interceptor filtering data
- Leetcode skimming: binary tree 16 (path sum)
- - Oui. Net Distributed Transaction and Landing Solution
- DP:树DP
- E. Singhal and Numbers(质因数分解)
- [C language] three implementations of quick sorting and optimization details
- kubernetes资源对象介绍及常用命令(五)-(ConfigMap&Secret)
猜你喜欢
解决Thinkphp框架应用目录下数据库配置信息修改后依然按默认方式连接
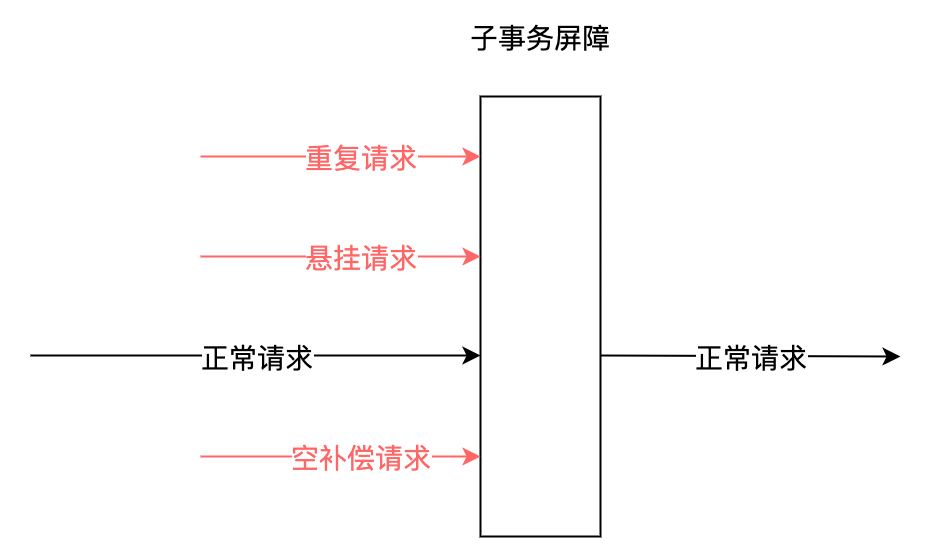
. Net distributed transaction and landing solution
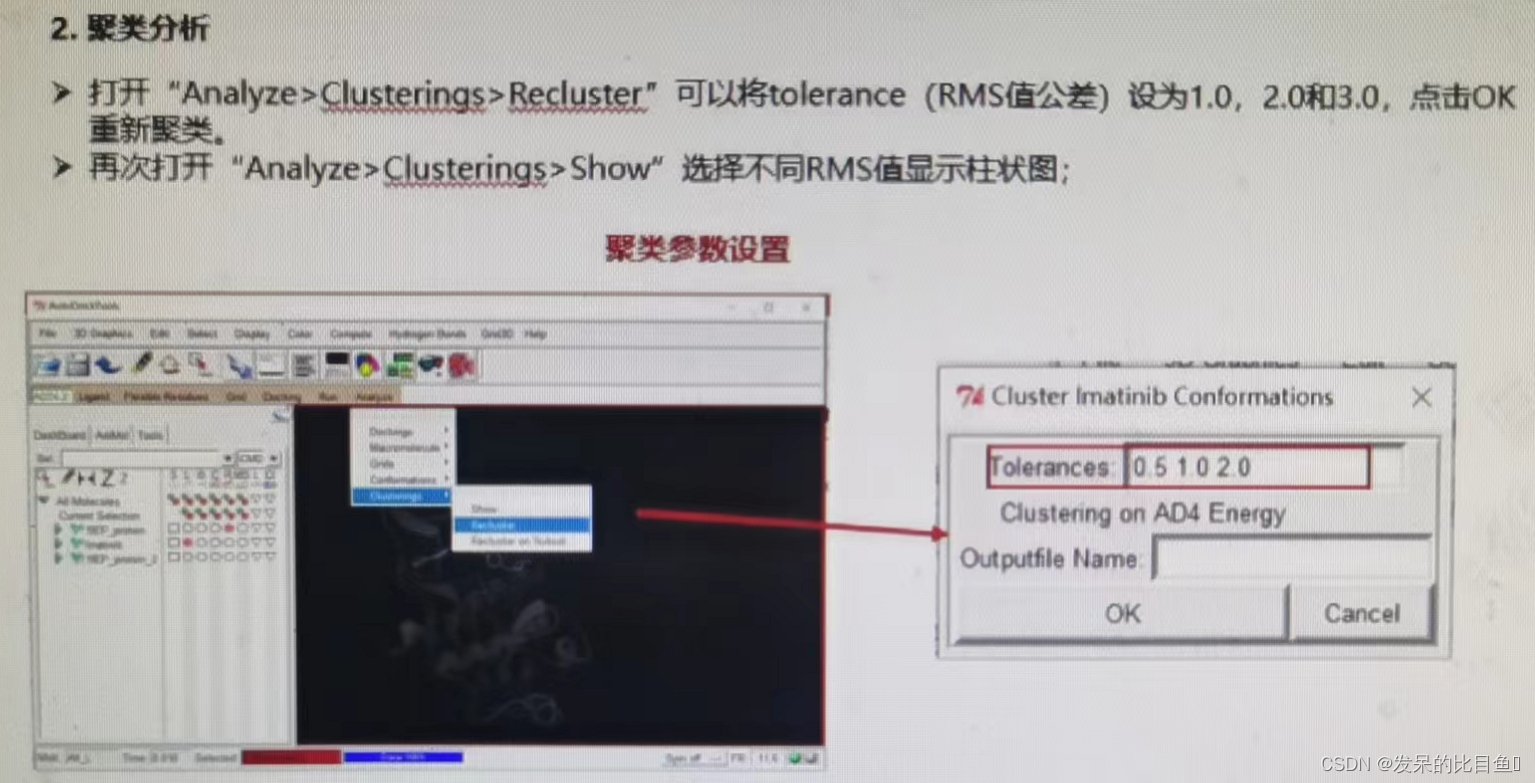
CADD课程学习(7)-- 模拟靶点和小分子相互作用 (半柔性对接 AutoDock)
Leetcode skimming: binary tree 17 (construct binary tree from middle order and post order traversal sequence)

leetcode刷题:二叉树14(左叶子之和)

JS implementation prohibits web page zooming (ctrl+ mouse, +, - zooming effective pro test)

kubernetes资源对象介绍及常用命令(五)-(ConfigMap&Secret)
建立自己的网站(16)
Leetcode skimming: binary tree 16 (path sum)
leetcode刷题:二叉树10(完全二叉树的节点个数)
随机推荐
c语言oj得pe,ACM入门之OJ~
c語言oj得pe,ACM入門之OJ~
【c语言】快速排序的三种实现以及优化细节
走入并行的世界
炒股开户最低佣金,低佣金开户去哪里手机上开户安全吗
Based on vs2017 and cmake GUI configuration, zxing and opencv are used in win10 x64 environment, and simple detection of data matrix code is realized
关于BRAM IP复位的优先级
1: Citation;
js方法传Long类型id值时会出现精确损失
[C language] string function and Simulation Implementation strlen & strcpy & strcat & StrCmp
处理文件和目录名
【数字IC验证快速入门】8、数字IC中的典型电路及其对应的Verilog描述方法
JS implementation prohibits web page zooming (ctrl+ mouse, +, - zooming effective pro test)
SecureRandom那些事|真伪随机数
Debezium series: record the messages parsed by debezium and the solutions after the MariaDB database deletes multiple temporary tables
计算lnx的一种方式
Bzoj 3747 poi2015 kinoman segment tree
Redis cluster simulated message queue
Leetcode skimming: binary tree 10 (number of nodes of a complete binary tree)
[quick start to digital IC Verification] 8. Typical circuits in digital ICs and their corresponding Verilog description methods