当前位置:网站首页>shiyou的数值分析作业
shiyou的数值分析作业
2020-11-08 08:04:00 【osc_4x0ulctb】
数值分析作业
突然想起来可以做做数值分析的作业,于是把室友的数值分析作业拿过来练手,写一篇博客分享一下。其实我这个菜鸟把程序写复杂了,有很多可以简化的地方,由于本菜鸟其它作业还没写完,就不去简化了,大家可以自行改正啦。
文章目录
数值分析上机题
首先说一下自己的疑惑,对于第一题python怎么实现对ln(x)直接调用求导呢?是直接用泰勒展开后对多项式求导吗?第二题是用Newton迭代法,要求出迭代初始值在什么范围可以得到收敛解,这里如果用迭代程序去实现的话也会比较麻烦,那有没有更好的方法去求解呢?希望有大神可以帮忙留言解惑,多谢。
一、题1——对数的近似求解
1.题目描述
**题目:**这里偷下懒,直接贴出原题的截图吧。

2.python实现
不多BB,程序在这:
import numpy as np
from sympy import * #用于求导积分等科学计算
import math as m
x = Symbol('x')#x 变量
t = Symbol('t')
y1 = 1/(1+x) #公式
y2 = -1/(1+x) #公式
y3 = 2/(1-x**2) #公式
def func(m):
res = m
for j in range(1,m):
res *= j
return res
def ln_Tyalor(y):
Tl_expr = y * (t-x)
for i in range(1, 10):
fac = func(i+1)
f_n = diff(y, x, i)
Tl_expr += (f_n / fac)*(t-x)**(i+1)
return Tl_expr.subs({
x:0})
#print(ln_Tyalor(y1))
sexpr1 = ln_Tyalor(y1)
sexpr2 = ln_Tyalor(y2)
sexpr3 = ln_Tyalor(y3)
A = sexpr1.subs({
t:1}).evalf()
B = sexpr2.subs({
t:-1/2}).evalf()
C = sexpr3.subs({
t:1/3}).evalf()
print('ln2的值:', m.log(2, m.e))
print('方程ln(1+x)的10阶泰勒展开计算结果为:', A,'\n','估计误差为:', abs(m.log(2, m.e)-A))
print('方程ln(1/(1+x))的10阶泰勒展开计算结果为:', B,'\n','估计误差为:', abs(m.log(2, m.e)-B))
print('方程ln((1+x)/(1-x))的10阶泰勒展开计算结果为:', C,'\n','估计误差为:', abs(m.log(2, m.e)-C))
3.输出结果
ln2的值: 0.6931471805599453
方程ln(1+x)的10阶泰勒展开计算结果为: 0.645634920634921
估计误差为: 0.0475122599250246
方程ln(1/(1+x))的10阶泰勒展开计算结果为: 0.693064856150793
估计误差为: 8.23244091517905e-5
方程ln((1+x)/(1-x))的10阶泰勒展开计算结果为: 0.693146047390827
估计误差为: 1.13316911820593e-6
一、题2——方程求根的Newton法
1.题目描述
**题目:**还是截图方便。

2.python实现
这个程序写的不好,由于写完后,exp()函数老是报错说:整型数据不是exp对象的属性,改了之后也没实现自己的想法,那就这样吧,没时间啦,大家自己搞吧。。。。。
import numpy as np
from sympy import * #用于求导积分等科学计算
import math as m
def f(x):
return 3*x**2 - m.exp(x) #该方程有3个根,初步估计在[-1,0],[0,1],[3,4]
def fdiff(x):
return 6*x - m.exp(x)
def g(x):
return 6*x - m.exp(x)#该方程有3个根,初步估计在[0,1],[2,3]
def gdiff(x):
return 6 - m.exp(x)
a = float(input('请输入计算区间的下界a(浮点型): '))
b = float(input('请输入计算区间的上界b(浮点型): '))
c = float(input('请输入迭代初始值(浮点型): '))
n = input('请输入要求解的函数,f代表f(x),g代表g(x): ')
if n =='f':
if f(a) * f(b)> 0:
print('在此区间内函数有多个根或者无根')
elif f(a) * f(b) == 0:
print('f(a) = ', '%f'%f(a))
print('f(b) = ', '%f'%f(b))
else:
fcount = 0
y = c - f(c) / fdiff(c)
while (abs(c - y) >= 0.5e-9) & (fdiff(c) != 0):
x2 = c - f(c) / fdiff(c)
y = c
c = x2
fcount += 1
print('函数给出的求根区间是:', [a, b])
print("函数f(x)的Newton迭代次数:%f,函数f(x)的迭代计算所得的根为:%.8f"%(fcount,c))
elif n =='g':
if g(a) * g(b)> 0:
print('在此区间内函数有多个根或者无根')
elif g(a) * g(b) == 0:
print('g(a) = ', '%f'%g(a))
print('g(b) = ', '%f'%g(b))
else:
gcount = 0
y = c - g(c) / gdiff(c)
while (abs(c - y) >= 0.5e-9) & (gdiff(c) != 0):
x2 = c - g(c) / gdiff(c)
y = c
c = x2
gcount += 1
print('函数给出的求根区间是:', [a, b])
print("函数g(x)的Newton迭代次数:%f,函数g(x)的迭代计算所得的根为:%.8f"%(gcount,c))
3.输出结果
这里说明一下,输入的[a, b]是你想判断该区间有没有根;c是迭代初始值;f代表f(x),g代表g(x);这几个参数请自己输入。
请输入计算区间的下界a(浮点型): -1.0
请输入计算区间的上界b(浮点型): 4.0
请输入迭代初始值(浮点型): -3.0
请输入要求解的函数,f代表f(x),g代表g(x): f
函数给出的求根区间是: [-1.0, 4.0]
函数f(x)的Newton迭代次数:7.000000,函数f(x)的迭代计算所得的根为:-0.45896227
一、题3——Hilbert矩阵的条件数
1.题目描述
**题目:**你懂的。

2.python实现
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['simhei']
n = int(input('请输入Hilbert方阵的最大维数:' ))
def max_sum_rows(X):
sum_row_list1 = []
for i in range(len(X)):
count = 0
for j in range(len(X)):
count += abs(X[i][j])
sum_row_list1.append(count)
return max(sum_row_list1)
inf_fanshu = []
Hilbert_cond = []
for i in range(1, n+1):
X = 1./(np.arange(1, i+1) + np.arange(0, i)[:, np.newaxis])
invX = np.linalg.inv(X)
a1 = max_sum_rows(invX)
a2 = max_sum_rows(X)
inf_fanshu.append(a2)
H_cond = a1 * a2
Hilbert_cond.append(H_cond)
#计算10,20……100的无穷范数条件数
Hilbert_cond_test = []
for j in range(n):
if (j+1)%10 == 0:
Hilbert_cond_test.append(Hilbert_cond[j])
print('生成维数从10,20……100的Hilbert矩阵的行范数条件数:\n', Hilbert_cond_test)
plt.title('Hilbert矩阵维数与条件数对数之间的关系')
plt.plot((list(range(1,n+1))), np.log(Hilbert_cond),c ='b', marker='*',label='拟合曲线')
plt.legend()
plt.xlabel('矩阵维度n')
plt.xticks(np.arange(0, n+1, 5))
plt.yticks(np.arange(0, 55, 5))
plt.ylabel('log(cond)')
plt.show()
#求解Hilbert方程的解和对应的无穷条件数
r_A_A_acc_list = []
r_B_list = []
r_cond = []
r_B_cond = []
for i in range(1,n+1):
A = np.ones((i,1))*1
X = 1. / (np.arange(1, i + 1) + np.arange(0, i)[:, np.newaxis])
B = X@A
A_acc = np.linalg.inv(X)@B
r_A_A_acc = A - A_acc
r_B = B - X @ A_acc
r_A_A_acc_list.append(r_A_A_acc)
r_B_list.append(r_B)
r_cond.append(abs(r_A_A_acc[:]).max()) #x-x_acc的无穷范数
r_B_cond.append(abs(r_B[:]).max())#b-Hx_acc的无穷范数
print('维数为10,50,100时的x-x_acc计算结果:\n', r_A_A_acc_list[9] ,r_A_A_acc_list[49] , r_A_A_acc_list[99])
print('维数为10,50,100时的b-Hx_acc计算结果:\n',r_B_list[9], r_B_list[49], r_B_list[99])
print('维数为10,50,100时的x-x_acc矩阵的无穷条件数计算结果:\n', r_cond[9], r_cond[49], r_cond[99])
print('维数为10,50,100时的b-Hx_acc矩阵的无穷条件数计算结果:\n', r_B_cond[9], r_B_cond[49], r_B_cond[99])
3.输出结果
输入你想计算的Hilbert方阵的最大维数就行,其它交给程序。
请输入Hilbert方阵的最大维数:100
生成维数从10,20……100的Hilbert矩阵的行范数条件数:
[35356847610517.12, 6.008376652086652e+18, 8.396589803249062e+18, 9.491653209312077e+19, 1.7763569870536153e+20, 1.9301974218850052e+21, 3.9847310708042826e+19, 1.3450693870678838e+20, 5.444272740462528e+19, 1.3244131088115743e+20]
这里输出的图片如下:
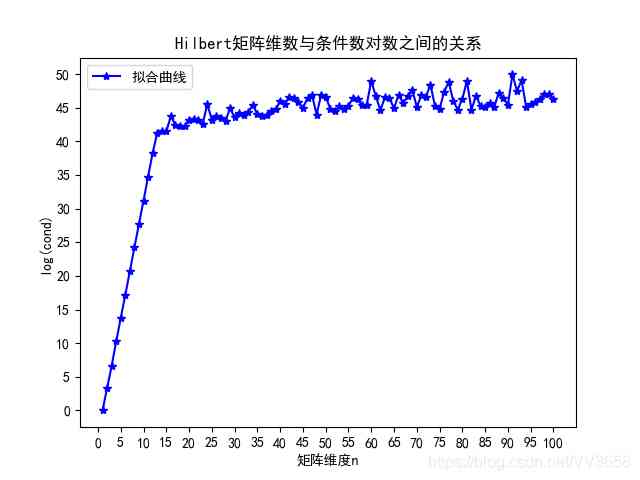
这里是第四问的输出结果:
维数为10,50,100时的x-x_acc计算结果:
[[-2.54168641e-04]
[ 2.16242671e-03]
[-5.54656982e-03]
[ 5.08880615e-03]
[ 9.15527344e-04]
[-4.02832031e-03]
[ 1.46484375e-03]
[ 4.88281250e-04]
[-1.22070312e-04]
[-6.10351562e-05]] [[ 8.01768149e+02]
[ 3.33788188e+04]
[-1.59537467e+06]
[ 1.98594595e+07]
[-1.31128704e+08]
·················
[-4.04700000e+03]
[ 6.50000000e+01]
[-2.25000000e+01]
[ 3.30000000e+01]
[-7.30000000e+01]] [[ 1.05255071e+04]
[-1.31934071e+06]
[ 4.56146227e+07]
[-7.42843201e+08]
[ 6.95696228e+09]
[-4.13027099e+10]
················
[-4.79000000e+02]
[ 5.12100000e+03]
[-1.91900000e+03]
[ 1.77000000e+02]]
维数为10,50,100时的b-Hx_acc计算结果:
[[1.27400597e-05]
[2.15601768e-05]
[1.73587501e-05]
[1.43429989e-05]
[1.23056437e-05]
[1.08422262e-05]
[9.72981380e-06]
[8.84754702e-06]
[8.12566450e-06]
[7.52108032e-06]] [[ 13.49201973]
[ 7.51301334]
[ -4.25849823]
[-14.49468816]
[-21.55733783]
[-26.46828937]
···············
[-28.3616173 ]
[-28.05340528]
[-27.75051982]
[-27.45291237]] [[-22.02594035]
[-22.62163018]
[-20.05848154]
[-17.70284588]
[-16.01064382]
[-14.79343569]
···············
[ -3.83066178]
[ -3.79759674]
[ -3.76500334]
[ -3.73286444]
[ -3.70119334]]
维数为10,50,100时的x-x_acc矩阵的无穷条件数计算结果:
0.00554656982421875 7824513409.0 998313040247.0
维数为10,50,100时的b-Hx_acc矩阵的无穷条件数计算结果:
2.1560176801216357e-05 38.404672581436365 22.62163018366762
结语
分享出来仅供相互学习,相互探讨,如所写有误,请多多包涵。希望能相互学习,共同进步,欢迎各位大佬留言评论。
版权声明
本文为[osc_4x0ulctb]所创,转载请带上原文链接,感谢
https://my.oschina.net/u/4321566/blog/4707852
边栏推荐
- 来自不同行业领域的50多个对象检测数据集
- Visual Studio 2015 未响应/已停止工作的问题解决
- Using subprocess residue in supervisor and python multiprocessing
- Basic operation of database
- leetcode之判断路径是否相交
- Got timeout reading communication packets解决方法
- GET,POST,PUT,DELETE,OPTIONS用法与说明
- VC6 compatibility and open file crash resolution
- nvm
- CPP (1) installation of cmake
猜你喜欢

Daily challenges of search engines_ 4_ External heterogeneous resources - Zhihu
These core technology of object-oriented, after you master it, you can have a good interview

scala 中 Future 的简单使用

On the stock trading of leetcode

Application of bidirectional LSTM in outlier detection of time series
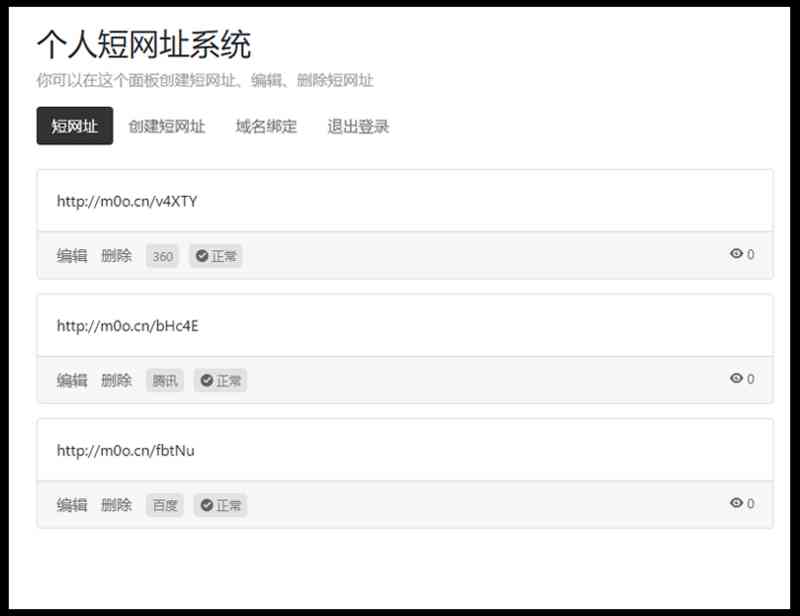
个人短网址生成平台 自定义域名、开启防红、统计访问量

5G+AR出圈,中国移动咪咕成第33届中国电影金鸡奖全程战略合作伙伴
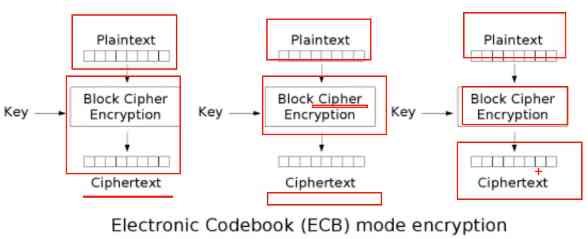
Cryptography - Shangsi Valley

M-end software product design considerations - Zhihu
模板链表类学习
随机推荐
Adobe Prelude / PL 2020 software installation package (with installation tutorial)
Face recognition: attack types and anti spoofing techniques
Wechat applet request reported 400 error @ requestbody failed to receive
nvm
Android 9.0/P WebView 多进程使用的问题
Blazor 准备好为企业服务了吗?
Python image recognition OCR
Game mathematical derivation AC code (high precision and low precision multiplication and division comparison) + 60 code (long long) + 20 point code (Full Permutation + deep search DFS)
Privacy violation and null dereference of fortify vulnerability
Data structure and sorting algorithm
微信昵称emoji表情,特殊表情导致列表不显示,导出EXCEL报错等问题解决!
Learn Scala if Else statement
Idea - the. IML file was not automatically generated by the project
A compilation bug brought by vs2015 Update1 update [existing solutions]
C expression tree (1)
Seven features of Python 3.9
QT hybrid Python development technology: Python introduction, hybrid process and demo
归纳一些比较好用的函数
laravel8更新之速率限制改进
Cryptography - Shangsi Valley