当前位置:网站首页>暴力递归到动态规划 08(小马走象棋)
暴力递归到动态规划 08(小马走象棋)
2022-08-03 00:26:00 【涛涛英语学不进去】

递归思路
考虑马儿的所有行程点,越界则不计入。
public int ways(int a, int b, int step) {
System.out.println(jump(a, b, 0, 0, step));
return process(a, b, 0, 0, step);
}
/** * @param a 目标位置x * @param b 目标位置y * @param i 当前位置i * @param j 当前位置j * @param step 剩余步数 step * @return 横9线,纵10线 * 9行10列 * [0-8] [0-9] */
private int jump(int a, int b, int i, int j, int step) {
if (step == 0) {
//当前是一种方法
return a == i && b == j ? 1 : 0;
}
// i j 跳跃情况:i+1,j+2 i+2,j+1 i-1,j+2 i-2,j+1 i+1,j-2 i+2,j-1
int upRightDown = i + 1 <= 9 && j + 2 <= 8 ? jump(a, b, i + 1, j + 2, step - 1) : 0;
int upRightUp = i + 2 <= 9 && j + 1 <= 8 ? jump(a, b, i + 2, j + 1, step - 1) : 0;
// i-2,j+1 i-2,j-1
int upLeftDown = i - 2 >= 0 && j + 1 <= 8 ? jump(a, b, i - 2, j + 1, step - 1) : 0;
int upLeftUp = i - 1 >= 0 && j + 2 <= 8 ? jump(a, b, i - 1, j + 2, step - 1) : 0;
// i-1,j-2 i-2,j-1
int downLeftDown = i - 1 >= 0 && j - 2 >= 0 ? jump(a, b, i - 1, j - 2, step - 1) : 0;
int downLeftUp = i - 2 >= 0 && j - 1 >= 0 ? jump(a, b, i - 2, j - 1, step - 1) : 0;
// i+1,j-2 i+2,j-1
int downRightDown = i + 1 <= 9 && j - 2 >= 0 ? jump(a, b, i + 1, j - 2, step - 1) : 0;
int downRightUp = i + 2 <= 9 && j - 1 >= 0 ? jump(a, b, i + 2, j - 1, step - 1) : 0;
return upRightDown + upRightUp + upLeftDown + upLeftUp + downLeftDown + downLeftUp + downRightDown + downRightUp;
}
简化
private int process(int a, int b, int i, int j, int step) {
if (i > 9 || j > 8 || i < 0 || j < 0) {
return 0;
}
if (step == 0) {
//当前是一种方法
return a == i && b == j ? 1 : 0;
}
// i j 跳跃情况:i+1,j+2 i+2,j+1 i-1,j+2 i-2,j+1 i+1,j-2 i+2,j-1
int ways = process(a, b, i + 1, j + 2, step - 1);
ways += process(a, b, i + 2, j + 1, step - 1);
// i-2,j+1 i-2,j-1
ways += process(a, b, i - 2, j + 1, step - 1);
ways += process(a, b, i - 1, j + 2, step - 1);
// i-1,j-2 i-2,j-1
ways += process(a, b, i - 1, j - 2, step - 1);
ways += process(a, b, i - 2, j - 1, step - 1);
// i+1,j-2 i+2,j-1
ways += process(a, b, i + 1, j - 2, step - 1);
ways += process(a, b, i + 2, j - 1, step - 1);
return ways;
}
动态规划
public int dp(int a, int b, int k) {
int[][][] dp = new int[10][9][k + 1];
//第一层填好
dp[a][b][0] = 1;
for (int step = 1; step <=k; step++) {
for (int i = 0; i < 10; i++) {
for (int j = 0; j < 9; j++) {
// i j 跳跃情况:i+1,j+2 i+2,j+1 i-1,j+2 i-2,j+1 i+1,j-2 i+2,j-1
int upRightDown = i + 1 <= 9 && j + 2 <= 8 ? dp[i + 1][j + 2][step - 1] : 0;
int upRightUp = i + 2 <= 9 && j + 1 <= 8 ? dp[i + 2][j + 1][step - 1] : 0;
// i-2,j+1 i-2,j-1
int upLeftDown = i - 2 >= 0 && j + 1 <= 8 ? dp[i - 2][j + 1][step - 1] : 0;
int upLeftUp = i - 1 >= 0 && j + 2 <= 8 ? dp[i - 1][j + 2][step - 1] : 0;
// i-1,j-2 i-2,j-1
int downLeftDown = i - 1 >= 0 && j - 2 >= 0 ? dp[i - 1][j - 2][step - 1] : 0;
int downLeftUp = i - 2 >= 0 && j - 1 >= 0 ? dp[i - 2][j - 1][step - 1] : 0;
// i+1,j-2 i+2,j-1
int downRightDown = i + 1 <= 9 && j - 2 >= 0 ? dp[i + 1][j - 2][step - 1] : 0;
int downRightUp = i + 2 <= 9 && j - 1 >= 0 ? dp[i + 2][j - 1][step - 1] : 0;
dp[i][j][step] = upRightDown + upRightUp + upLeftDown + upLeftUp + downLeftDown + downLeftUp + downRightDown + downRightUp;
}
}
}
return dp[0][0][k];
}
边栏推荐
猜你喜欢
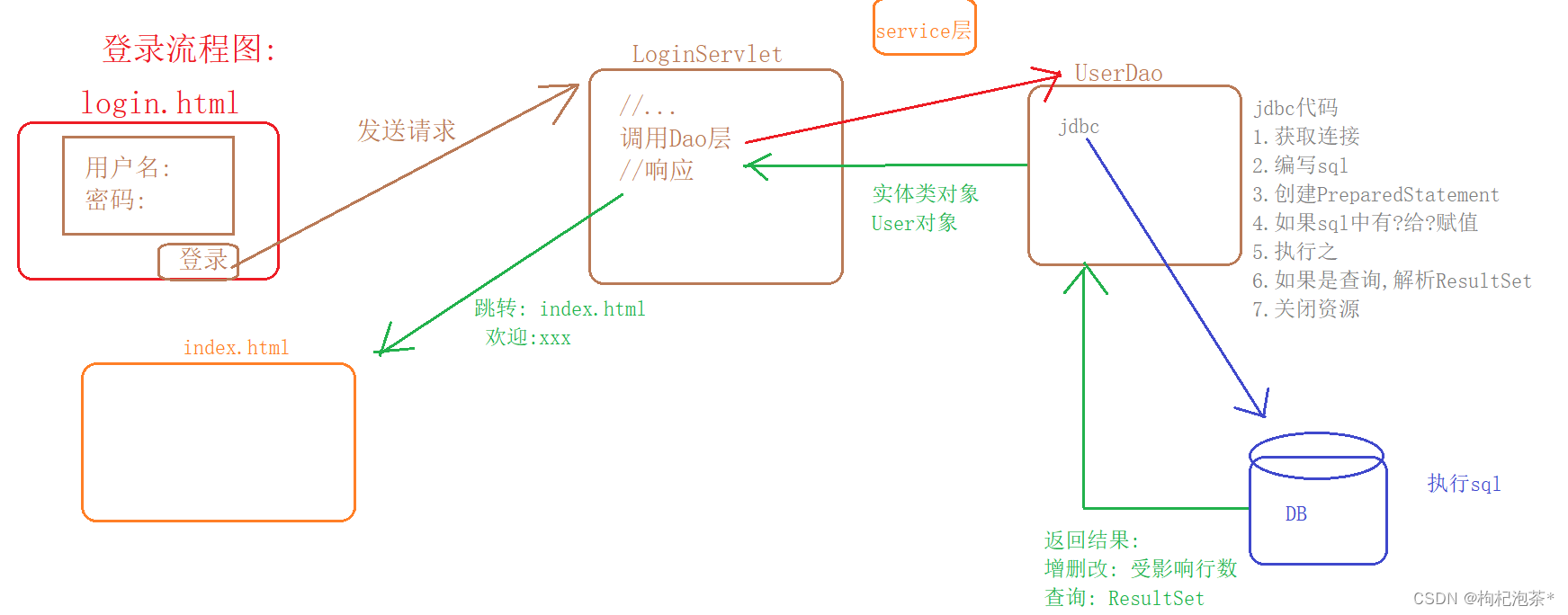
Servlet——请求(request)与响应(response)
Flink / Scala - 使用 CountWindow 实现按条数触发窗口
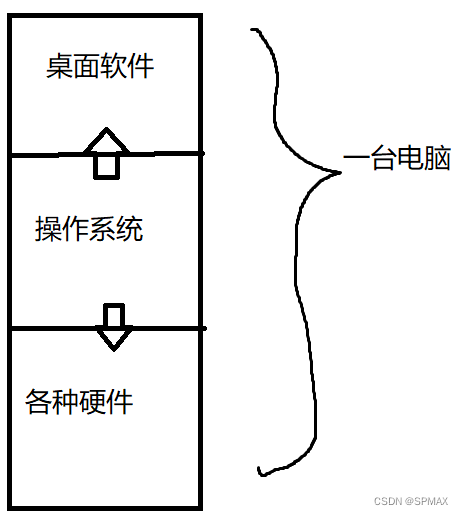
【多线程】线程与进程、以及线程进程的调度

解决错误:Optional int parameter ‘pageSize‘ is present but cannot be translated into a null value due to
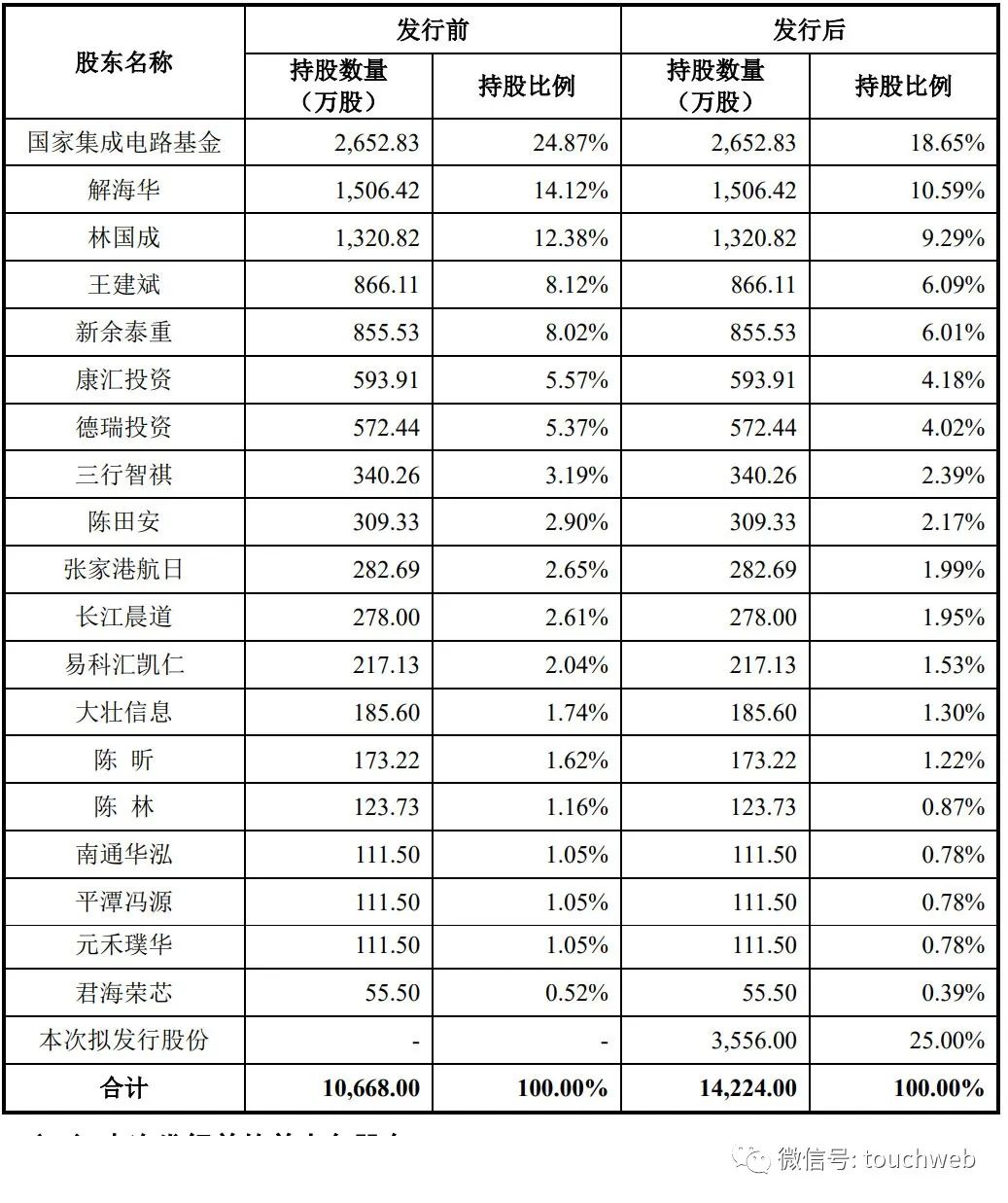
德邦科技通过注册:年营收5.8亿 国家集成电路基金为大股东

2022 开放原子全球开源峰会 | 麒麟信安携手openEuler助力开源产业繁荣发展
esp32和ros2基础篇草稿-micro-ros-
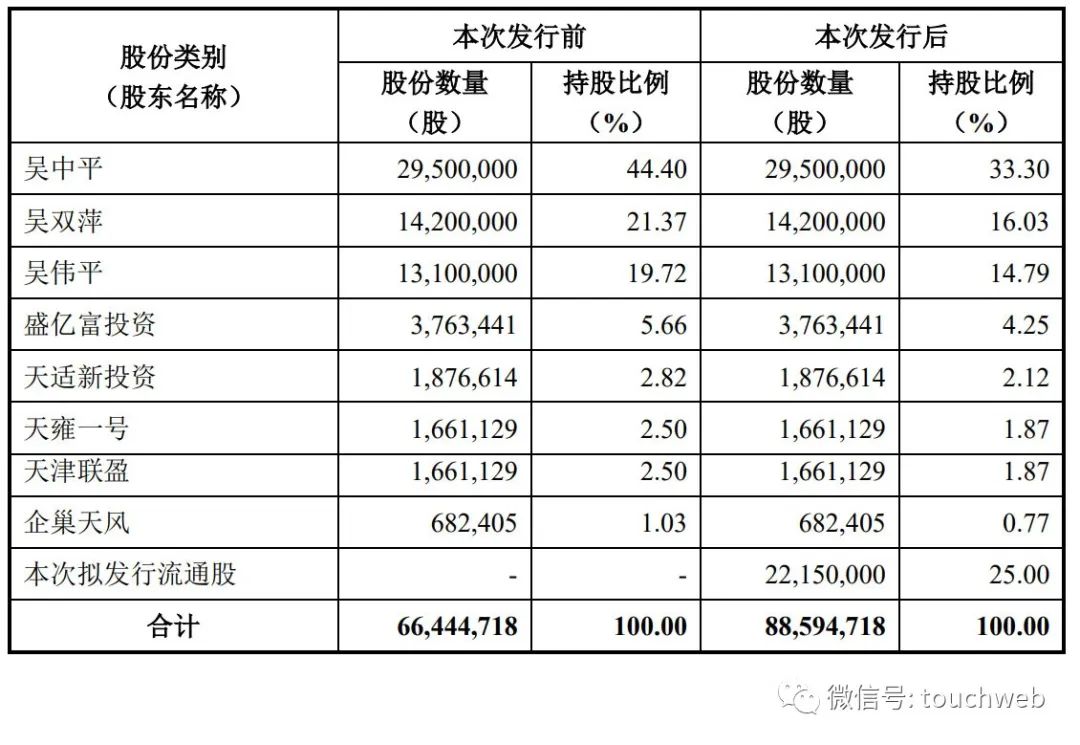
中科磁业IPO过会:年营收5.5亿 吴中平家族持股85%

并发模型和I/O模型介绍
SAP ABAP Gateway Client 里 OData 测试的 PUT, PATCH, MERGE 请求有什么区别
随机推荐
线上交流丨稀疏神经网络:实践和理论(青源Talk第23期 汪张扬)
flutter 时间戳转日期
Oracle 暴跌,倒下了!
2022年8月2日——使用idea搭建servlet+jsp项目
10. SAP ABAP OData 服务如何支持修改(Update)操作
【系统架构设计师】第三章 数据库系统
牛客网剑指offer刷题练习之链表中环的入口结点
【MySQL —— 数据库约束】
【飞控开发高级教程2】疯壳·开源编队无人机-遥控整机代码走读、编译与烧写
matlab常微分方程在传染病建模中的应用
面试题 08.07. 无重复字符串的排列组合 ●●
Visual Studio中vim模拟器
vue3的keepAlive缓存组件
【软考 系统架构设计师】软件架构设计① 软件架构的概念
【QT】自定义工程封装成DLL并如何调用(带ui界面的)
Day117. Shangyitong: Generate registered order module
升级版的冒泡排序:鸡尾酒排序(快乐小时排序)
关于地图GIS开发事项的一次实践整理(上)
【图像分类】2021-EfficientNetV2 CVPR
7.29