Judging the connectivity of undirected graphs by the method of similar Union and set search

Connectivity of graphs

In an undirected graph , There is a path from any vertex to other vertices , It means that it is connected

Union checking set

See Baidu Encyclopedia for specific concepts Union checking set
Let's put it simply , It was independent at the beginning N In a collection of elements , Put together elements that have certain associations , Make them have a common parent node （ In fact, it is the same root node ）, After the use of search set, we will see a forest （ Even if there is only one tree ）. For the connectivity of graphs , And if you find only one tree left under the collection , Then this graph is connected

Topic introduction

Here, I use a method similar to union search to solve a problem of judging the connectivity of graphs , Link here ： Connectivity
Yes, of course , If you want to do this problem , You don't need to follow the meaning of the question until you enter two 0 It's over , Just judge a graph

The original question is as follows ：

The time limit ：C/C++ 1 second , Other languages 2 Second space limit ：C/C++ 64M, Other languages 128M

 Given an undirected graph and all its edges , Determine whether all vertices of the graph are connected .

Input description :
The first row of each set of data is two integers n and m（0<=n<=1000）.n Represents the number of vertices in a graph ,m Represents the number of edges in a graph . Then there are m Row data , Each line has two values x and y（0<x, y <=n）, It means a vertex x and y Connected to a , The vertices are numbered from 1 Start calculating . The input does not guarantee that the edges are repeated .

Output description :
Input data for each group , If all the vertices are connected , Output "YES", Otherwise output "NO".
Example 1
Input
4 3
1 2
2 3
3 2
3 2
1 2
2 3
0 0

Output
NO
YES

Similar to the method of searching sets

It is slightly different from the method introduced by Baidu Encyclopedia , I used a better way to understand , Of course, the cost is that the time efficiency will be lower . It's like this ：

step	practice
1	The parent node number of each node entered is the same as its number
2	If the parent node numbers of two nodes are the same , There is no need to perform the following two steps
3	For two connected points , Let their parent node number be the number of the second point
4	Make the previous parent node number the same as the parent node number of the first node equal to the parent node number of the second node in the second step

I don't think what's said above is too convoluted , Here is an example ：

The picture above has 4 A vertex and 4 side , At the beginning, the numbering of child nodes and parent nodes is ：

Suppose that the connection between the two points we input is ：
1 2
2 3
1 4
1 3

The first input 1 2 after ,1 Vertex sum 2 The parent node number of vertex No. is 2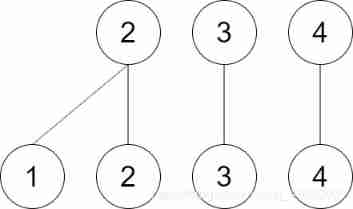

Because there is no parent node number of vertex and 1 The parent node number at the beginning of vertex No. 1 is the same , So you can see the second input

The second input 2 3 after ,2 Vertex sum 3 The parent node number of vertex No. is 3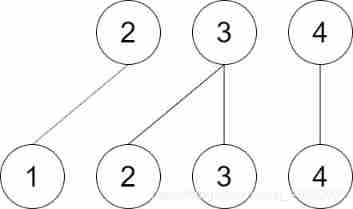

But here 1 No. vertex parent node number and 2 The parent node number at the beginning of vertex No. 1 is the same , Now? 2 The parent node number of node No. becomes 3 The parent node number of node No , So the 1 The parent node number of node No. is also made 3 The parent node number of node No , Pictured ：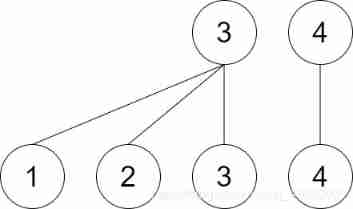

The third input 1 4 after ,1 The parent node number of vertex No. becomes 4 The parent node number of vertex No , namely 4, Pictured ：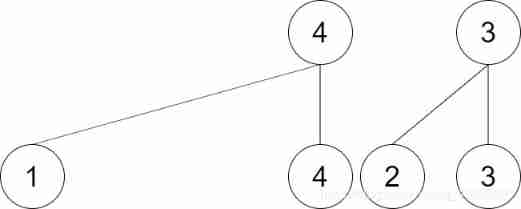

But after the second input ,2 Number and 3 The parent node number of vertex No. and 1 Node No. has the same parent node number , So here we need to change the parent node number of these two vertices to and 1 Node number is the same , namely 4 The parent node number of vertex No -4

The fourth input 1 3, Because their parent node numbers are already the same , The last two steps in the table need not be performed

After using this method , If the parent node number is the same as the vertex number, only 1 individual , That is, there is only one tree , Then this undirected graph is connected

The code is as follows ：（1）JAVA edition ：

import java.util.Scanner;

public class Main {
    
// Judge connected graph by union set method 
// Use a forest with weak relationship to represent trees , Don't worry about the left and right child nodes 
public static int[] root=new int[1001];
static int edge,vertex;

public static void union(int v1,int v2) {
    
	// Make two connected points have the same root node 
	int fx=root[v1];
	int fy=root[v2];
	if(fx!=fy){
    root[v1]=root[v2];
	// Make the nodes before the change connected together 
	for(int i=1;i<=vertex;++i) {
    
		if(root[i]==fx)
			root[i]=root[v2];}
	}
}
public static void main(String args[]) {
    
	Scanner input=new Scanner(System.in);
	boolean loop=true;
	while(loop) {
    
	vertex=input.nextInt();
	edge=input.nextInt();
	if(edge==0&&vertex==0) {
    
		loop=false;continue;
	}
	// Initialize root 
	for(int i=1;i<=vertex;++i)
		root[i]=i;
	for(int i=1;i<=edge;++i) {
    
		int v1=input.nextInt();
		int v2=input.nextInt();
		union(v1, v2);
	}
	// Judge connectivity 
	int k=0;
	for(int i=1;i<=vertex;++i) 
		if(root[i]==i)++k;
	
	if(k==1)System.out.println("YES");
		else System.out.println("NO");
}
	input.close();
	
}
}

（2）C++ edition ：

#include <iostream>
using namespace std;
// Use and look up sets , The root node is initialized to 0
int root[1001] = {
     0 };
int vertex, edge;// The number of vertices and edges 
void bind(int v1, int v2) {
    
	// Make two connected points have the same root node 
	int root1 = root[v1];
	int root2 = root[v2];
	if (root1 == root2)return;
	else {
    
		root[v1] = root[v2];
		for (int i = 1; i <= vertex; ++i) {
    
			if (root[i] == root1)
				root[i] = root[v2];
		}
	}
}
int main()
{
       
	while (true) {
    
		cin >> vertex >> edge;
		if (vertex == 0 && edge == 0)break;
		// Initialize root 
		for (int i = 1; i <= vertex; ++i)
			root[i] = i;
		for (int i = 1; i <= edge; ++i) {
    
			int v1, v2;
			cin >> v1 >> v2;
			bind(v1, v2);
		}
		// Judge connectivity 
		int k = 0;
		for (int i = 1; i <= vertex; ++i)
			if (root[i] == i)++k;

		if (k == 1)cout<<("YES");
		else cout<<("NO");
	
	}
	return 0;
}

I hope it will be helpful to your study ~