当前位置:网站首页>Deep understanding of softmax
Deep understanding of softmax
2022-07-08 02:17:00 【Strawberry sauce toast】
Preface
This code is based on Pytorch Realization .
One 、softmax Definition and code implementation of
1.1 Definition
s o f t m a x ( x i ) = e x p ( x i ) ∑ j n e x p ( x j ) softmax(x_i) = \frac{exp(x_i)}{\sum_j^nexp(x_j)} softmax(xi)=∑jnexp(xj)exp(xi)
1.2 Code implementation
def softmax(X):
''' Realization softmax Input X The shape of is [ Number of samples , Output vector dimension ] '''
return torch.exp(X) / torch.sum(torch.exp(X), dim=1).reshape(-1, 1)
>>> X = torch.randn(5, 5)
>>> y = softmax(X)
>>> torch.sum(y, dim=1)
tensor([1.0000, 1.0000, 1.0000, 1.0000])
Two 、softmax The role of

softmax The output of the linear layer can be normalized and calibrated : Ensure that the output is nonnegative and the sum is 1.
Because if you directly regard the non normalized output as probability , Will exist 2 Some questions :
- The output of the linear layer does not limit the sum of the output numbers of each neuron to 1;
- Depending on the input , The output of the linear layer may be negative .
this 2 Point violates the basic axiom of probability .
3、 ... and 、softmax Overflow on (overflow) Overflow with bottom (underflow)
3.1 It spills over
When x i x_i xi When the value of is too large , The value of index operation is too large , If it is beyond the accuracy range , Then overflow .
>>> torch.exp(torch.tensor([1000]))
tensor([inf])
3.2 underflow
When the vector x \boldsymbol x x Each element of x i x_i xi When the values of are negative numbers with large absolute values , be e x p ( x i ) exp(x_i) exp(xi) The value of is very small, and it is taken down beyond the accuracy range 0, The denominator ∑ j e x p ( j ) \sum_jexp(j) ∑jexp(j) The values for 0.
>>> X = torch.ones(1, 3) * (-1000)
>>> softmax(X)
tensor([[nan, nan, nan]])
3.3 Avoid spillovers
Reference resources 1 The technique in :
- Find vector x \boldsymbol x x Maximum of :
c = m a x ( x ) c=max(\boldsymbol x) c=max(x) - s o f t m a x softmax softmax The molecules of 、 Divide the denominator by c c c
s o f t m a x ( x i − c ) = e x p ( x i − c ) ∑ j n e x p ( x j − c ) = e x p ( x i ) e x p ( − c ) ∑ j n e x p ( x i ) e x p ( − c ) = s o f t m a x ( x i ) softmax(x_i - c) = \frac{exp(x_i-c)}{\sum_j^nexp(x_j-c)}=\frac{exp(x_i)exp(-c)}{\sum_j^nexp(x_i)exp(-c)}=softmax(x_i) softmax(xi−c)=∑jnexp(xj−c)exp(xi−c)=∑jnexp(xi)exp(−c)exp(xi)exp(−c)=softmax(xi)
After the above transformation , The maximum value of the molecule becomes e x p ( 0 ) = 1 exp(0)=1 exp(0)=1, Avoid upper overflow ;
At least + 1 +1 +1, Avoid denominator 0 Cause lower overflow .
∑ j n e x p ( x j − c ) = e x p ( x i − c ) + e x p ( x 2 − c ) + . . . + e x p ( x m a x − c ) = e x p ( x 1 − c ) + e x p ( x 2 − c ) + . . . + 1 \sum_j^nexp(x_j-c) =exp(x_i-c)+exp(x_2-c)+...+exp(x_{max}-c)\\ =exp(x_1-c) + exp(x_2-c)+...+1 j∑nexp(xj−c)=exp(xi−c)+exp(x2−c)+...+exp(xmax−c)=exp(x1−c)+exp(x2−c)+...+1
def softmax_trick(X):
c, _ = torch.max(X, dim=1, keepdim=True)
return torch.exp(X - c) / torch.sum(torch.exp(X - c), dim=1).reshape(-1, 1)
>>> X = torch.tensor([[-1000, 1000, -1000]])
>>> softmax_trick(X)
tensor([0., 1., 0.])
>>> softmax(X)
tensor([[0., nan, 0.]])
pytorch The implementation of has been done to prevent overflow , therefore , Its operation results are similar to softmax_trick Agreement .
import pytorch.nn.functional as F
>>> X = torch.tensor([[-1000., 1000., -1000.]])
>>> F.softmax(X, dim=1)
tensor([[0., 1., 0.]])
3.4 Log-Sum_Exp Trick2( take log operation )
1. Avoid spillage
Logarithmic operation can change multiplication into addition , namely : l o g ( x 1 x 2 ) = l o g ( x 1 ) + l o g ( x 2 ) log(x_1x_2) = log(x_1) + log(x_2) log(x1x2)=log(x1)+log(x2). When two very small numbers x 1 、 x 2 x_1、x_2 x1、x2 Multiplying time , The product becomes smaller , If the accuracy is exceeded, it will overflow ; The logarithmic operation turns the product into addition , Reduce the risk of lower overflow .
2. Avoid overflow
l o g − s o f t m a x log-softmax log−softmax The definition of :
l o g − s o f t m a x = l o g [ s o f t m a x ( x i ) ] = l o g ( e x p ( x i ) ∑ j n e x p ( x j ) ) = x i − l o g [ ∑ j n e x p ( x j ) ] \begin{aligned} log-softmax &=log[softmax(x_i)] \\ &= log(\frac{exp(x_i)}{\sum_j^nexp(x_j)}) \\ &=x_i - log[\sum_j^nexp(x_j)] \end{aligned} log−softmax=log[softmax(xi)]=log(∑jnexp(xj)exp(xi))=xi−log[j∑nexp(xj)]
Make y = l o g ∑ j n e x p ( x j ) y=log\sum_j^nexp(x_j) y=log∑jnexp(xj), When x j x_j xj When the value of is too large , y y y There is a risk of spillover , therefore , with 3.3 The same in Trick:
y = l o g ∑ j n e x p ( x j ) = l o g ∑ j n e x p ( x j − c ) e x p ( c ) = c + l o g ∑ j n e x p ( x j − c ) \begin{aligned} y &= log\sum_j^nexp(x_j) \\ & = log\sum_j^nexp(x_j-c)exp(c) \\ & = c +log\sum_j^nexp(x_j-c) \end{aligned} y=logj∑nexp(xj)=logj∑nexp(xj−c)exp(c)=c+logj∑nexp(xj−c)
When c = m a x ( x ) c=max(\boldsymbol x) c=max(x) when , Avoid overflow .
here , l o g − s o f t m a x log-softmax log−softmax The calculation formula of becomes :( In fact, it is equivalent to directly 3.3 Chaste Trick Take the logarithm )
l o g − s o f t m a x = ( x i − c ) − l o g ∑ j n e x p ( x j − c ) log-softmax = (x_i-c)-log\sum_j^nexp(x_j-c) log−softmax=(xi−c)−logj∑nexp(xj−c)
Code implementation :
def log_softmax(X):
c, _ = torch.max(X, dim=1, keepdim=True)
return X - c - torch.log(torch.sum(torch.exp(X-c), dim=1, keepdim=True))
>>> X = torch.tensor([[-1000., 1000., -1000.]])
>>> torch.exp(log_softmax(X))
tensor([[0., 1., 0.]])
# pytorch API Realization
>>> torch.exp(F.log_softmax(X, dim=1))
tensor([[0., 1., 0.]])
3.5 log-softmax And softmax The difference between 3
combination 3.3 Chaste Trick And my own understanding :
- stay pytorch In the implementation of ,softmax The result of the operation is equivalent to log_softmax The result of is exponentially calculated
>>> X = torch.tensor([[-1000., 1000., -1000.]])
>>> torch.exp(F.log_softmax(X, dim=1)) == F.softmax(X)
tensor([[True, True, True]])
- Use l o g log log It is more convenient to derive after operation , It can speed up the speed of back propagation 4
∂ ∂ x i l o g s o f t m a x = ∂ ∂ x i [ x i − l o g ∑ j n e x p ( x j ) ] = 1 − s o f t m a x ( x i ) \begin{aligned} \frac{\partial}{\partial x_i}logsoftmax&=\frac{\partial}{\partial x_i} [{x_i - log\sum_j^nexp(x_j)]} \\ &= 1 - softmax(x_i) \end{aligned} ∂xi∂logsoftmax=∂xi∂[xi−logj∑nexp(xj)]=1−softmax(xi)
边栏推荐
- OpenGL/WebGL着色器开发入门指南
- Talk about the cloud deployment of local projects created by SAP IRPA studio
- Unity 射线与碰撞范围检测【踩坑记录】
- 发现值守设备被攻击后分析思路
- COMSOL --- construction of micro resistance beam model --- final temperature distribution and deformation --- addition of materials
- Semantic segmentation | learning record (5) FCN network structure officially implemented by pytoch
- What are the types of system tests? Let me introduce them to you
- 分布式定时任务之XXL-JOB
- [error] error loading H5 weight attributeerror: 'STR' object has no attribute 'decode‘
- WPF custom realistic wind radar chart control
猜你喜欢

Many friends don't know the underlying principle of ORM framework very well. No, glacier will take you 10 minutes to hand roll a minimalist ORM framework (collect it quickly)
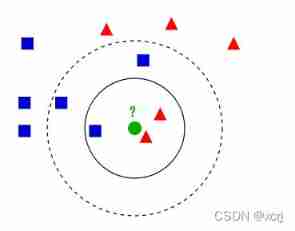
Ml self realization /knn/ classification / weightlessness

JVM memory and garbage collection-3-runtime data area / heap area

MQTT X Newsletter 2022-06 | v1.8.0 发布,新增 MQTT CLI 和 MQTT WebSocket 工具

力争做到国内赛事应办尽办,国家体育总局明确安全有序恢复线下体育赛事

谈谈 SAP iRPA Studio 创建的本地项目的云端部署问题

银行需要搭建智能客服模块的中台能力,驱动全场景智能客服务升级

leetcode 869. Reordered Power of 2 | 869. Reorder to a power of 2 (state compression)
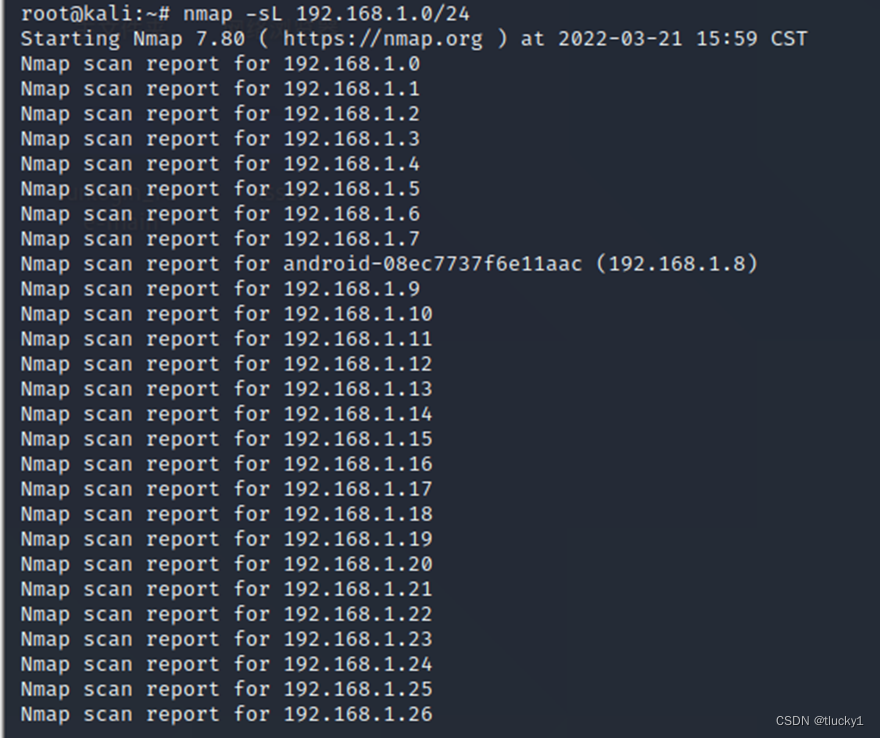
nmap工具介紹及常用命令

Keras' deep learning practice -- gender classification based on inception V3
随机推荐
EMQX 5.0 发布:单集群支持 1 亿 MQTT 连接的开源物联网消息服务器
魚和蝦走的路
Semantic segmentation | learning record (5) FCN network structure officially implemented by pytoch
Master go game through deep neural network and tree search
喜欢测特曼的阿洛
leetcode 869. Reordered Power of 2 | 869. Reorder to a power of 2 (state compression)
谈谈 SAP 系统的权限管控和事务记录功能的实现
Disk rust -- add a log to the program
nmap工具介绍及常用命令
云原生应用开发之 gRPC 入门
Kwai applet guaranteed payment PHP source code packaging
Where to think
Semantic segmentation | learning record (2) transpose convolution
力争做到国内赛事应办尽办,国家体育总局明确安全有序恢复线下体育赛事
C language -cmake cmakelists Txt tutorial
阿锅鱼的大度
[knowledge atlas paper] minerva: use reinforcement learning to infer paths in the knowledge base
Ml self realization / logistic regression / binary classification
How to use diffusion models for interpolation—— Principle analysis and code practice
直接加比较合适