当前位置:网站首页>Call pytorch API to complete linear regression
Call pytorch API to complete linear regression
2022-07-07 08:07:00 【Students who don't want to be bald】
Pytorch Complete the basic model
The goal is
- know Pytorch in Module How to use
- know Pytorch How to use the optimizer class in
- know Pytorch The common use of loss function in
- Know how to GPU Run code on
- Be able to say common optimizers and their principles
1. Pytorch Complete the model API
In the previous part , We achieved it ourselves through torch Back propagation and parameter updating are completed by the relevant methods of , stay pytorch Some more flexible and simple objects are preset in , Let's construct the model 、 Define loss , Optimization loss, etc
So next , Let's take a look at the commonly used API
1.1 nn.Module
nn.Modul yes torch.nn A class provided , yes pytorch We Custom network A base class of , There are many useful methods defined in this class , Let's inherit this class and define the network very simply
When we customize the network , There are two ways to pay special attention :
__init__Need to callsuperMethod , Inherits the properties and methods of the parent classfarwardMethod must implement , The process used to define the forward computation of our network
Use the front one y = wx+b An example of the model is as follows :
from torch import nn
class Lr(nn.Module):
def __init__(self):
super(Lr, self).__init__() # Inherited parent class init Parameters of
self.linear = nn.Linear(1, 1)
def forward(self, x):
out = self.linear(x)
return out
Be careful :
nn.Linearby torch Predefined linear model , Also known as Full link layer , The parameter passed in is the number of inputs , Number of outputs (in_features, out_features), It doesn't count (batch_size Columns of )nn.ModuleDefined__call__Method , The implementation is to callforwardMethod , namelyLrExample , Can be called directly by passed in parameters , It's actually calling thetaforwardMethod and pass in parameters
# Instantiation model
model = Lr()
# Incoming data , The result of the calculation is
predict = model(x)
1.2 Optimizer class
Optimizer (optimizer), It can be understood as torch The method encapsulated for us to update parameters , For example, the common random gradient descent (stochastic gradient descent,SGD)
Optimizer classes are composed of torch.optim Provided , for example
torch.optim.SGD( Parameters , Learning rate )torch.optim.Adam( Parameters , Learning rate )
Be careful :
- Parameters can be used
model.parameters()To get , Get all the data in the modelrequires_grad=TrueParameters of - Optimize the use of classes
- Instantiation
- Gradient of all parameters , Set the value to 0
- Back propagation calculation gradient
- Update parameter values
Examples are as follows :
optimizer = optim.SGD(model.parameters(), lr=1e-3) #1. Instantiation
optimizer.zero_grad() #2. Set the gradient to 0
loss.backward() #3. Calculate the gradient
optimizer.step() #4. Update the value of the parameter
1.3 Loss function
The previous example is a regression problem ,torch Many loss functions are also predicted in
- Mean square error :
nn.MSELoss(), Often used in regression problems - Cross entropy loss :
nn.CrossEntropyLoss(), Commonly used for classification problems
Usage method :
model = Lr() #1. Instantiation model
criterion = nn.MSELoss() #2. Instantiate the loss function
optimizer = optim.SGD(model.parameters(), lr=1e-3) #3. Instantiate the optimizer class
for i in range(100):
y_predict = model(x_true) #4. Calculate the predicted value forward
loss = criterion(y_true,y_predict) #5. Call the loss function to pass in the real value and the predicted value , Get the loss result
optimizer.zero_grad() #5. The current loop parameter gradient is set to 0
loss.backward() #6. Calculate the gradient
optimizer.step() #7. Update the value of the parameter
1.4 Complete the linear regression code
import torch
from torch import nn
from torch import optim
import numpy as np
from matplotlib import pyplot as plt
# 1. Defining data
x = torch.rand([50,1])
y = x*3 + 0.8
#2 . Defining models
class Lr(nn.Module):
def __init__(self):
super(Lr,self).__init__()
self.linear = nn.Linear(1,1)
def forward(self, x):
out = self.linear(x)
return out
# 2. Instantiation model ,loss, And optimizer
model = Lr()
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=1e-3)
#3. Training models
for i in range(30000):
out = model(x) #3.1 Get predictions
loss = criterion(y,out) #3.2 Calculate the loss
optimizer.zero_grad() #3.3 The gradient goes to zero
loss.backward() #3.4 Calculate the gradient
optimizer.step() # 3.5 Update gradient
if (i+1) % 20 == 0:
print('Epoch[{}/{}], loss: {:.6f}'.format(i,30000,loss.data))
#4. Model to evaluate
model.eval() # Set the model to evaluation mode , Prediction mode
predict = model(x)
predict = predict.data.numpy()
plt.scatter(x.data.numpy(),y.data.numpy(),c="r")
plt.plot(x.data.numpy(),predict)
plt.show()
Output is as follows :
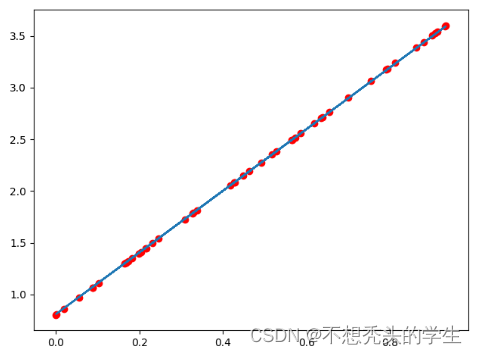
Be careful :
model.eval() Indicates that the model is set to the evaluation mode , Prediction mode
model.train(mode=True) Indicates that the model is set to training mode
In the current linear regression , There is no difference between the above
But in other models , The parameters of training and prediction will be different , At that time, we need to tell the program whether we are training or predicting , For example, there are Dropout,BatchNorm When
2. stay GPU Run code on
When the model is too large , Or when there are too many parameters , To speed up your training , Often use GPU To train
At this point, our code needs to be adjusted slightly :
Judge GPU Is it available
torch.cuda.is_available()torch.device("cuda:0" if torch.cuda.is_available() else "cpu") >>device(type='cuda', index=0) # Use gpu >>device(type='cpu') # Use cpuCompare the model parameters with input Data into cuda Type of support for
model.to(device) x_true.to(device)stay GPU The calculation result is also cuda Data type of , We need to convert to numpy perhaps torch Of cpu Of tensor type
predict = predict.cpu().detach().numpy()detach()The effect and data Similarity of , howeverdetach()It's a deep copy ,data It's a value , Is a shallow copy
The modified code is as follows :
import torch
from torch import nn
from torch import optim
import numpy as np
from matplotlib import pyplot as plt
import time
# 1. Defining data
x = torch.rand([50,1])
y = x*3 + 0.8
#2 . Defining models
class Lr(nn.Module):
def __init__(self):
super(Lr,self).__init__()
self.linear = nn.Linear(1,1)
def forward(self, x):
out = self.linear(x)
return out
# 2. Instantiation model ,loss, And optimizer
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
x,y = x.to(device),y.to(device)
model = Lr().to(device)
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=1e-3)
#3. Training models
for i in range(300):
out = model(x)
loss = criterion(y,out)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if (i+1) % 20 == 0:
print('Epoch[{}/{}], loss: {:.6f}'.format(i,30000,loss.data))
#4. Model to evaluate
model.eval() #
predict = model(x)
predict = predict.cpu().detach().numpy() # Turn into numpy Array
plt.scatter(x.cpu().data.numpy(),y.cpu().data.numpy(),c="r")
plt.plot(x.cpu().data.numpy(),predict,)
plt.show()
3. Introduction to common optimization algorithms
3.1 Gradient descent algorithm (batch gradient descent BGD)
Each iteration needs to send all samples into , The advantage is that each iteration takes into account all the samples , What we do is global optimization , But it is possible to achieve local optimization .
3.2 Random gradient descent method (Stochastic gradient descent SGD)
Aiming at the disadvantage that the training speed of gradient descent algorithm is too slow , A stochastic gradient descent algorithm is proposed , Random gradient descent algorithm is to randomly extract a group of samples , Update once according to the gradient after training , Then take another group , Update again , When the sample size is extremely large , It may not be necessary to train all the samples to obtain a model with a loss value within an acceptable range .
torch Medium api by :torch.optim.SGD()
3.3 Small batch gradient descent (Mini-batch gradient descent MBGD)
SGD It's much faster , But there are also problems , Because the training of a single sample may bring a lot of noise , bring SGD It's not going to be optimization every time , Therefore, it may converge quickly at the beginning of training , But after training for a period of time, it will become very slow . On this basis, a small batch gradient descent method is proposed , It is to randomly select a small batch of samples for training each time , Not a group , This ensures both the effect and the speed .
3.4 Momentum method
mini-batch SGD Although this algorithm can bring good training speed , But when you reach the best, you can't always really reach the best , But hovering around the best .
Another drawback is mini-batch SGD We need to choose an appropriate learning rate , When we use a small learning rate , It will cause the network to converge too slowly during training ; When we adopt a large learning rate , It will cause the amplitude optimized during training to skip the range of the function , That is, it is possible to skip the best . What we hope is that when the network is optimized, the loss function of the network has a good convergence speed and does not swing too much .
therefore Momentum The optimizer can just solve the problem we face , It is mainly a moving exponential weighted average based on gradient , Smoothing the gradient of the network , Make the swing amplitude of the gradient smaller .
\begin{align*}
&gradent = 0.8\nabla w + 0.2 history_gradent &,\nabla w Represents the current gradient \
&w = w - \alpha* gradent &,\alpha It means the learning rate
\end{align*}
( notes :t+1 Of course histroy_gradent For the first time t Time of gradent)
3.5 AdaGrad
AdaGrad The algorithm is to square the gradient of each iteration of each parameter and accumulate it in the square , Divide the global learning rate by this number , As a dynamic update of learning rate , So as to achieve Adaptive learning rate The effect of
\begin{align*}
&gradent = history_gradent + (\nabla w)^2 \
&w = w - \frac{\alpha}{\sqrt{gradent}+\delta} \nabla w ,&\delta Is a small constant , For numerical stability, set to approximately 10^{-7}
\end{align*}
3.6 RMSProp
Momentum In the optimization algorithm , Although the problem of large swing range in optimization is preliminarily solved , In order to further optimize the loss function, there is a problem that the swing amplitude is too large , And further accelerate the convergence speed of the function ,RMSProp The algorithm uses the square weighted average for the gradient of parameters .
\begin{align*}
& gradent = 0.8history_gradent + 0.2(\nabla w)^2 \
& w = w - \frac{\alpha}{\sqrt{gradent}+\delta} \nabla w
\end{align*}
3.7 Adam
Adam(Adaptive Moment Estimation) The algorithm is to Momentum Algorithm and RMSProp An algorithm used in combination with algorithms , How much swing can be achieved to prevent gradient , At the same time, it can also increase the convergence rate
\begin{align*}
& 1. You need to initialize the cumulant and square cumulant of the gradient \
& v_w = 0,s_w = 0 \
& 2. The first t In round training , We can first calculate Momentum and RMSProp Parameter update for :\
& v_w = 0.8v + 0.2 \nabla w \qquad,Momentum Calculated gradient \
& s_w = 0.8s + 0.2(\nabla w)^2 \qquad,RMSProp Calculated gradient \
& 3. After processing the values , obtain :\
& w = w - \frac{\alpha}{\sqrt{s_w}+\delta} v_w
\end{align*}
torch Medium api by :torch.optim.Adam()
3.8 Effect demonstration :

It can be calculated that Momentum and RMSProp Parameter update for :\
& v_w = 0.8v + 0.2 \nabla w \qquad,Momentum Calculated gradient \
& s_w = 0.8s + 0.2(\nabla w)^2 \qquad,RMSProp Calculated gradient \
& 3. After processing the values , obtain :\
& w = w - \frac{\alpha}{\sqrt{s_w}+\delta} v_w
\end{align*}
$$
torch Medium api by :torch.optim.Adam()
3.8 Effect demonstration :
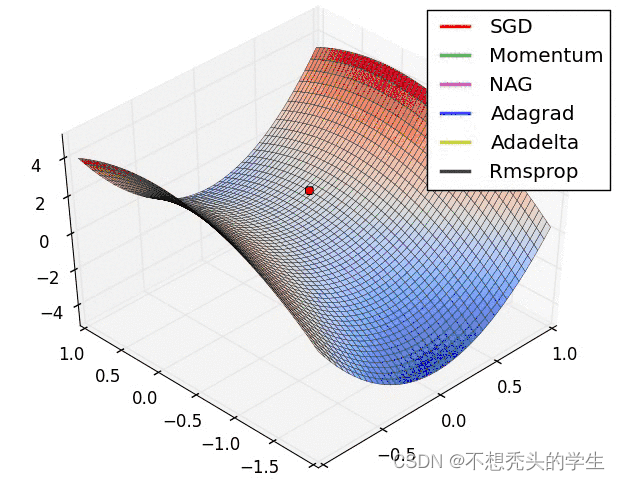
边栏推荐
- [UVM basics] summary of important knowledge points of "UVM practice" (continuous update...)
- Quickly use Jacobo code coverage statistics
- ZCMU--1492: Problem D(C语言)
- 力扣(LeetCode)187. 重复的DNA序列(2022.07.06)
- [quickstart to Digital IC Validation] 15. Basic syntax for SystemVerilog Learning 2 (operator, type conversion, loop, Task / Function... Including practical exercises)
- Explore dry goods! Apifox construction ideas
- Qt学习26 布局管理综合实例
- Dedecms collects content without writing rules
- Merging binary trees by recursion
- Network learning (III) -- highly concurrent socket programming (epoll)
猜你喜欢
![[matlab] when matrix multiplication in Simulink user-defined function does not work properly, matrix multiplication module in module library can be used instead](/img/e3/cceede6babae3c8a24336c81d98aa7.jpg)
[matlab] when matrix multiplication in Simulink user-defined function does not work properly, matrix multiplication module in module library can be used instead
Cnopendata American Golden Globe Award winning data
Force buckle 145 Binary Tree Postorder Traversal
2022 tea master (intermediate) examination questions and mock examination

json 数据展平pd.json_normalize
Padavan manually installs PHP
Empire CMS collection Empire template program general
Li Kou interview question 04.01 Path between nodes

Detailed explanation of Kalman filter for motion state estimation
uniapp 移动端强制更新功能
随机推荐
Linux Installation MySQL 8.0 configuration
Lattice coloring - matrix fast power optimized shape pressure DP
Recursive method constructs binary tree from middle order and post order traversal sequence
The legend about reading the configuration file under SRC
互动送书-《Oracle DBA工作笔记》签名版
这5个摸鱼神器太火了!程序员:知道了快删!
【数字IC验证快速入门】12、SystemVerilog TestBench(SVTB)入门
快解析内网穿透为文档加密行业保驾护航
【数字IC验证快速入门】13、SystemVerilog interface 和 program 学习
【数字IC验证快速入门】11、Verilog TestBench(VTB)入门
Empire CMS collection Empire template program general
Search for an element in a binary search tree (BST)
运放电路的反馈电阻上并联一个电容是什么作用
Recursive method to construct binary tree from preorder and inorder traversal sequence
Qt学习28 主窗口中的工具栏
Codeforce c.strange test and acwing
数据库实时同步利器——CDC(变化数据捕获技术)
2022 welder (elementary) judgment questions and online simulation examination
Record a stroke skin bone error of the skirt
Linux server development, MySQL index principle and optimization