The largest matrix (H) in a brush 143 monotone stack 84 histogram

 subject ：
 Given  n  Nonnegative integers , It is used to indicate the height of each column in the histogram . Each column is adjacent to each other , And the width is  1 .
 In this histogram , The maximum area of a rectangle that can be outlined .
--------------------------

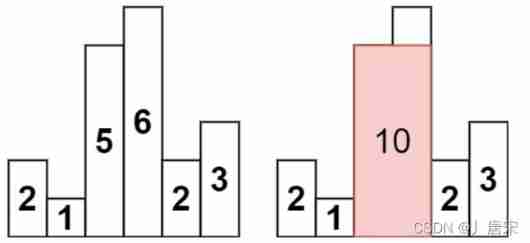
 Input ：heights = [2,1,5,6,2,3]
 Output ：10
 explain ： The largest rectangle is the red area in the figure , Area is  10

 Input ： heights = [2,4]
 Output ： 4
 
 Tips ：

1 <= heights.length <=105
0 <= heights[i] <= 104
--------------------
 reflection ：
 This topic and 42.  Rainwater collection , Are two topics that echo each other from afar , All suggestions should be done carefully ,
 There are many similarities in principle , But there are differences in details , It can deepen the understanding of monotone stack ！

 Dynamic programming ：
 The writing method of dynamic planning of this topic is the overall idea and 42.  It is consistent to receive rainwater , But more than 42.  It's harder to catch rain .
 The difficulty lies in recording each column   The first one on the left is smaller than the subscript of the column , Instead of the first one on the left less than the height of the column .
 So you need to cycle through , That is, the following is used in the process of searching while, Please see the following notes for details ,
 Sorting out ideas in problem solving ：42.  Rainwater collection   Has been introduced in .

class Solution {
    
public:
    int largestRectangleArea(vector<int>& heights) {
    
        vector<int> minLeftIndex(heights.size());
        vector<int> minRightIndex(heights.size());
        int size = heights.size();

        //  Record each column   The first one on the left is smaller than the subscript of the column 
        minLeftIndex[0] = -1; //  Note here that initialization , Prevent the following while Dead cycle 
        for (int i = 1; i < size; i++) {
    
            int t = i - 1;
            //  This is not for if, But the process of constantly looking to the left 
            while (t >= 0 && heights[t] >= heights[i]) t = minLeftIndex[t];
            minLeftIndex[i] = t;
        }
        //  Record each column   The first one on the right is smaller than the subscript of the column 
        minRightIndex[size - 1] = size; //  Note here that initialization , Prevent the following while Dead cycle 
        for (int i = size - 2; i >= 0; i--) {
    
            int t = i + 1;
            //  This is not for if, But the process of constantly looking to the right 
            while (t < size && heights[t] >= heights[i]) t = minRightIndex[t];
            minRightIndex[i] = t;
        }
        //  Sum up 
        int result = 0;
        for (int i = 0; i < size; i++) {
    
            int sum = heights[i] * (minRightIndex[i] - minLeftIndex[i] - 1);
            result = max(sum, result);
        }
        return result;
    }
};

 Monotonic stack ：
 The solution of local monotone stack and the problem of receiving rainwater echo each other from afar .

 Why do you say that ,42.  Rainwater collection   Is to find the first column on the left and right sides of each column that is greater than the height of the column ,
 And this problem is to find the first column smaller than the column on the left and right sides of each column .

 Here we come to the important properties of monotone stack , Is the order in the monotone stack , Is it from small to large or from large to small .

 In the problem solution 42.  Rainwater collection   In, I explained the monotonous stack of rainwater from the top of the stack （ Elements pop up from the top of the stack ） The order to the bottom of the stack should be from small to large .

 Then, because this problem is to find the first column smaller than the column on the left and right sides of each column , So from the top of the stack （ Elements pop up from the top of the stack ）
 The order to the bottom of the stack should be from large to small ！
 Let me give you an example , Pictured ：

 Only the order from big to small in the stack , To ensure that the top element of the stack finds the first column on the left and right that is smaller than the top element of the stack .

 So the order of this monotonous stack is just the opposite of that of receiving rain .

 At this time, you should find that it is actually 
 To the top of the stack   and 
 The next element at the top of the stack and 
 The three elements to be stacked form the height and width of the maximum area we require 

 Understand this , I have a good grasp of monotone stack .

 Except that the order of elements in the stack is different from that of rainwater , The rest of the logic is almost the same ,
 In the problem solution 42.  I have explained all aspects of monotonous stack in detail , I won't repeat it here .

 The rest is to analyze the following three situations ：

 Situation 1 ： Current traversal elements heights[i] Less than the top of the stack element heights[st.top()] The situation of 
 Situation two ： Current traversal elements heights[i] Equal to the top element of the stack heights[st.top()] The situation of 
 Situation three ： Current traversal elements heights[i] Greater than the top element of the stack heights[st.top()] The situation of 
-----------------
 Code ：
 Dynamic programming ：
class Solution {
    
	public int largestRectangleArea(int[] heights) {
    
		int length = heights.length;
		int[] minLeftIndex = new int[length];
		int[] maxRightIndex = new int[length];
		// Record the first subscript on the left that is smaller than the column 
		minLeftIndex[0] = -1;
		for (int i = 1; i < length; i++) {
    
			int t = i - 1;
			// This is not for if  But the national policy of constantly looking to the right 
			while (t >= 0 && heights[t] >= heights[i]) t = minLeftIndex[t];
			minLeftIndex[i] = t;
		} 
		// Record each column   The first one on the right is smaller than the subscript of the column 
		maxRightIndex[length - 1] = length;
		for (int i = length - 2; i >= 0; i--) {
    
			int t = i + 1;
			while (t < length && heights[t] >= heights[i]) t = maxRightIndex[t];
			maxRightIndex[i] = t;
		}
		// Sum up 
		int result = 0;
		for (int i = 0; i < length; i++) {
    
			int sum = heights[i] * (maxRightIndex[i] - minLeftIndex[i] - 1);
			result = Math.max(sum, result);
		}
		return result;
	}
}
 Monotonic stack ：
class Solution {
    
	public int largestRectangleArea(int[] heights) {
    
		Stack<Integer> stack = new Stack<>();
		// Array capacity ,  Add an element to the head and tail 
		int[] newHeights = new int[heights.length + 2];
		newHeights[0] = 0;
		newHeights[newHeights.length - 1] = 0;
		for (int index = 0; index < heights.length; index++) {
    
			newHeights[index + 1] = heights[index];
		}
		heights = newHeights;

		stack.push(0);
		int result = 0;
		// The first element is already on the stack ,  From the subscript 1 Start 
		for (int i = 1; i < heights.length; i++) {
    
			// Be careful heights[i]  Is and heights[stack.pop()]  Compare  stack.pop() It's a subscript 
			if (heights[i] > heights[stack.peek()]) {
    
				stack.push(i);
			}else if (heights[i] == heights[stack.peek()]) {
    
				stack.pop();//  This can be added , Can not add , The effect is the same , Different ideas 
				stack.push(i);
			}else {
    
				while (heights[i] < heights[stack.peek()]) {
    // Note that while
					int mid = stack.peek();
					stack.pop();
					int left = stack.peek();
					int right = i;
					int w = right - left - 1;
					int h = heights[mid];
					result = Math.max(result, w * h);
				}
				stack.push(i);
			}
		}
		return result;
	}
}

LC