当前位置:网站首页>[classic example] binary tree recursive structure classic topic collection @ binary tree
[classic example] binary tree recursive structure classic topic collection @ binary tree
2022-07-06 04:48:00 【Ah, Xiaobian】
Classic title
Xiao Bian has something to say : These topics are all about the understanding and application of binary tree recursive traversal structure , Are very classic topics .
Do a few things and you will feel , At present, I can't run away from all the topics , Recursion is nothing more than , Process the current node - It may be to do some operations / Maybe making some judgments is often out of condition , Then there is the recursive left subtree 、 Recursive right subtree ( notes : The first, middle and last sequence changes according to the topic ),and Empty nodes are often recursive jumps .
Recursion seems hard to think of , At least three months ago, I first learned that I didn't draw recursive expansion graphs. I was dizzy in some places , Up to now, hand it directly in your mind , There is still a little progress , Do a few and you'll feel it . But the time complexity of recursion , Sometimes some optimization can be done , They are all written in the article , This is what I need to continue to practice .
Text begins @ Does Xiao Bian still love programming
Always
1. Single valued binary trees
1.1 subject
Topic link : Single valued binary trees

1.2 Ideas and solutions
Divide and conquer :
- Single valued binary trees = root Equal to the value of left and right children + The left subtree is a single valued binary tree + The right subtree is a single valued binary tree
- The youngest question with an answer : Blank nodes ; root And the value of left and right children
bool isUnivalTree(struct TreeNode* root){
if(root == NULL)
return true;
if(root->left && root->left->val != root->val)
return false;
if(root->right && root->right->val != root->val)
return false;
return isUnivalTree(root->left) && isUnivalTree(root->right);
}
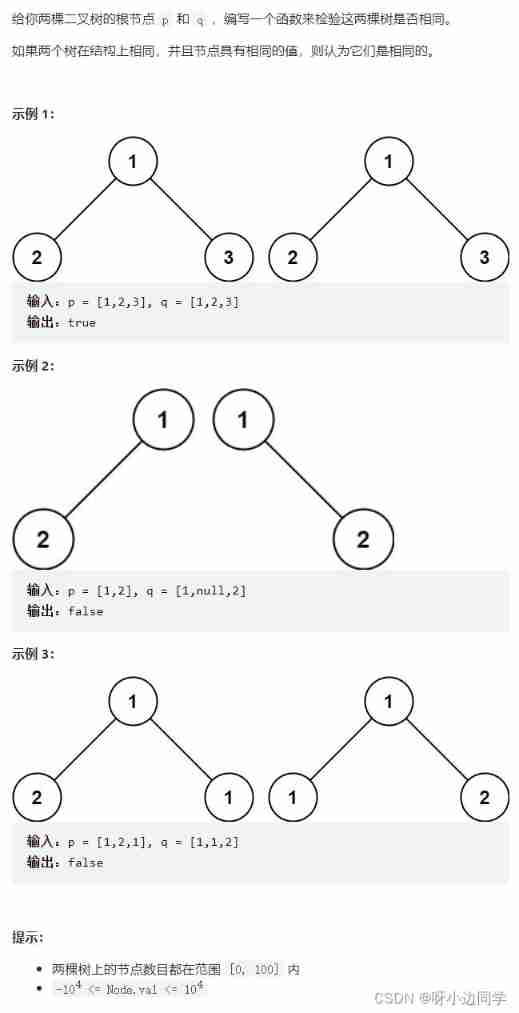
2. The same binary tree
2.1 subject
Topic link : Same tree
2.2 Ideas and solutions
Divide and conquer :
- The same binary tree = Compare the roots of two trees + Recursive left subtree ( Whether the left subtree of two trees is the same binary tree )+ Recursive right subtree ( Whether the right subtree of two trees is the same binary tree )
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
if(p == NULL && q == NULL)
return true;
if(p == NULL || q == NULL)
return false; // If you can walk here p and q One of them must be empty
// Coming here means p and q It must not be empty
if(p->val != q->val)
return false;
return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
}
This topic must be well understood , The mirror binary tree behind it is a small deformation ; Determine whether it is a subtree of another tree , It also needs to be used as a sub function to judge whether it is equal .
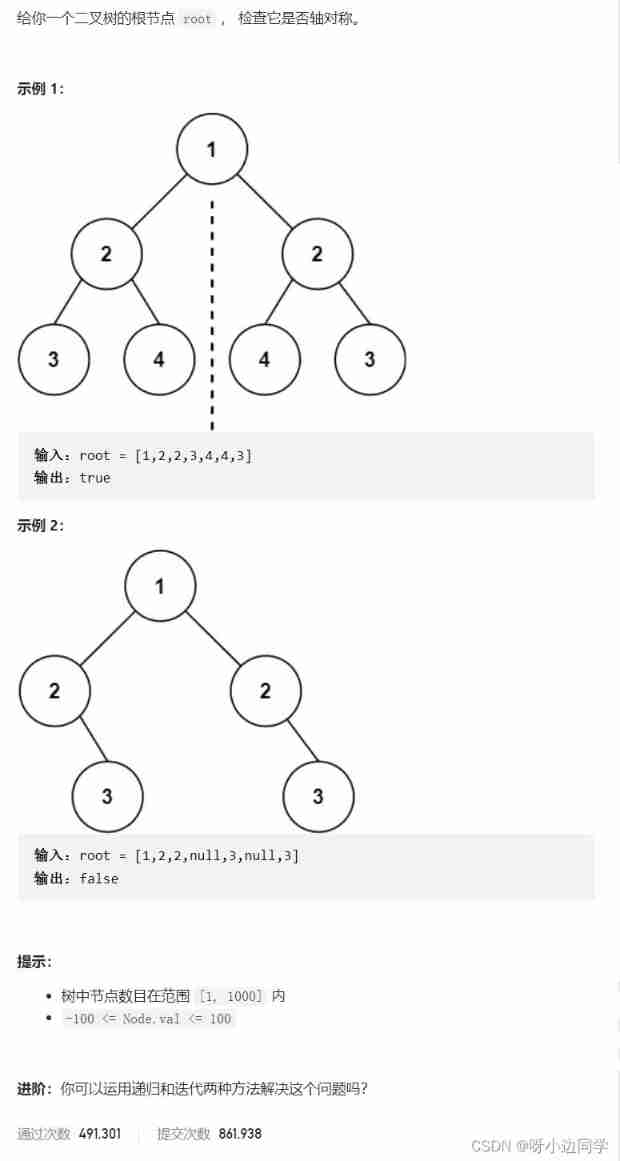
3. Mirror binary tree
3.1 subject
Topic link : Symmetric binary tree
3.2 Ideas and solutions
Whether it is a mirror binary tree , In fact, we should compare the left and right Two Whether the subtree is symmetrical . Can you feel , This is the same as whether the previous question is The same binary tree It's like , Just here is to compare whether the symmetrical nodes are the same .
In the original function interface, we are Recursion doesn't work Of , So write a sub function . This subfunction is The same binary tree Small deformation of .
bool _isSymmetric(struct TreeNode* p, struct TreeNode* q){
if(p == NULL && q == NULL)
return true;
if(p == NULL || q == NULL)
return false;
if(p->val != q->val)
return false;
return _isSymmetric(p->right, q->left) && _isSymmetric(p->left,q->right);
}
bool isSymmetric(struct TreeNode* root){
if(root == NULL)
return true;
return _isSymmetric(root->left,root->right);
}
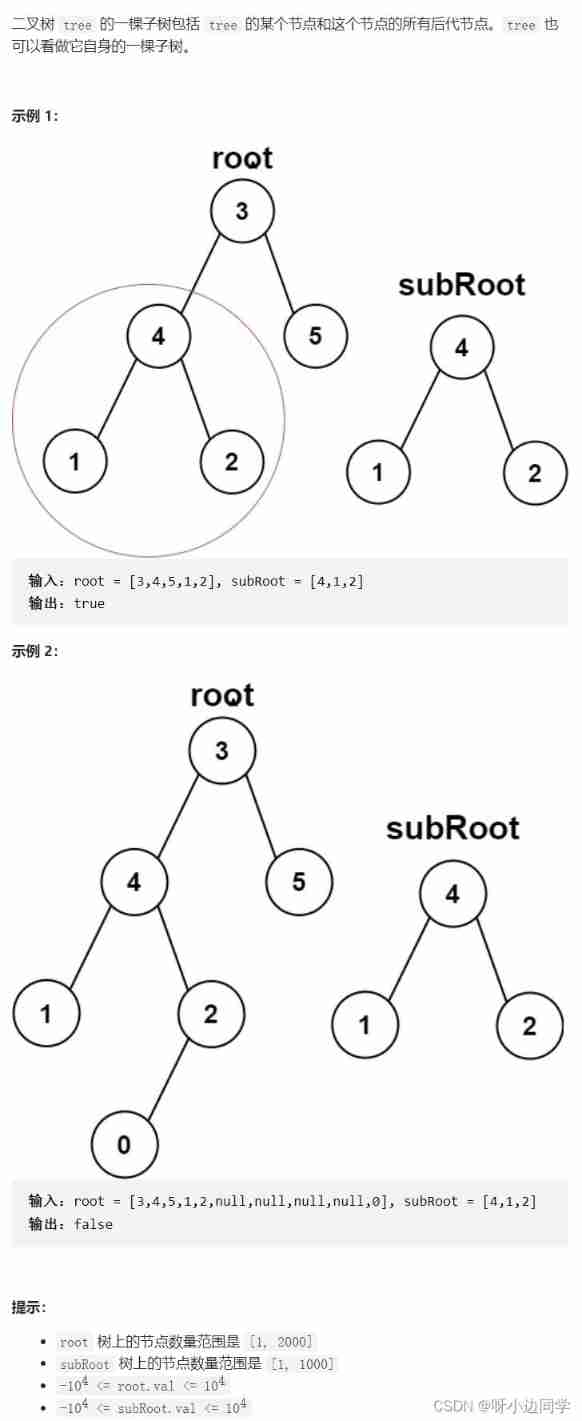
4. The subtree of another tree
4.1 subject
Topic link : The subtree of another tree
4.2 Ideas and solutions
use root Every subtree of the tree is associated with sub Compare . Here we will also use the subfunction of judging the same binary tree .
Divide and conquer :
- The subtree of the current node and subTree Is it the same + Recursive left subtree + Recursive right subtree
- Recursive termination condition : The subtree of the current node and subTree identical , It means that there is a subtree
bool _isSubtree(struct TreeNode* p, struct TreeNode* q){
if(p == NULL && q == NULL)
return true;
if(p == NULL || q == NULL)
return false;
if(p->val != q->val)
return false;
return _isSubtree(p->left,q->left) && _isSubtree(p->right,q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
// eureka
if(_isSubtree(root,subRoot))
return true;
if(root->left && isSubtree(root->left,subRoot))
return true;
if(root->right && isSubtree(root->right,subRoot))
return true;
return false;
}
Time complexity analysis : Suppose the scale is N
Calculate the time complexity of recursion , Formula is Number of recursions * Number of recursive calls per time , Pay attention to mental calculation .
- What is the time complexity of the best case ?O(N).
- It's equal as soon as it comes in
- The roots of each subtree are not equal , Just compare N Cigen
- What is the time complexity of the worst case ?O(N^2)
root Each subtree of follows subRoot Every time ,isSameTree Each time, the last node is different .
You can also write like this ——
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
if(root == NULL)
return false;
// eureka
if(isSameTree(root,subRoot))
return true;
return isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);
}
4.3 reflection
This is related to The lookup value is x The node of Very similar .
They are all , Compare with the current node first , Equal and return ; If it is not equal, go to the left tree to find , Left tree found , Just go back to , If the left tree is not found , Then go to the right tree to find . It's just that the comparison here is not a value , It is root The subtree of , Call a function to compare . Is a more complex search problem .
// The binary tree lookup value is x The node of
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
return NULL;
if (root->data == x)
return root;
// Recursion don't lose the return value , And pay attention to efficiency
BTNode* leftRet = BinaryTreeFind(root->left, x);
if (leftRet)
return leftRet;
BTNode* rightRet = BinaryTreeFind(root->right, x);
if (rightRet)
return rightRet;
return NULL;
}
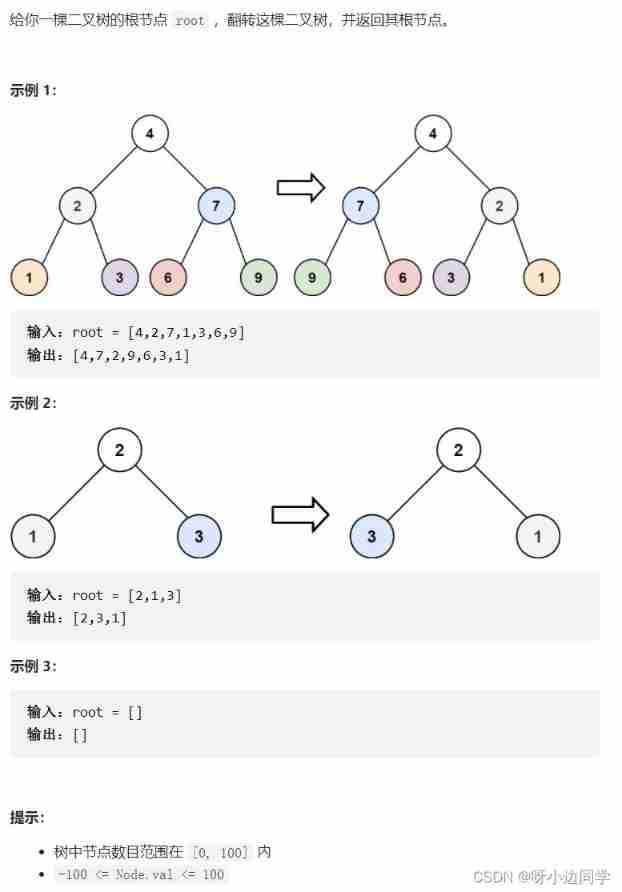
5. Flip binary tree
5.1 subject
Topic link : Flip binary tree
5.2 Ideas and Solutions
In fact! , The recursive structure of this tree is too much except for experience , There are still feelings .
Divide and conquer :
- Flip binary tree = Flip the left and right chains of the current node + Recursive left subtree ( Flip the left subtree ) + Recursive right subtree ( Flip the right subtree )
- Indivisible subproblem : Blank nodes
struct TreeNode* invertTree(struct TreeNode* root){
if(root == NULL)
return NULL;
struct TreeNode* tmp = root->left;
root->left = root->right;
root->right = tmp;
invertTree(root->left);
invertTree(root->right);
return root;
}
6. Balanced binary trees
6.1 subject
Topic link : Balanced binary trees
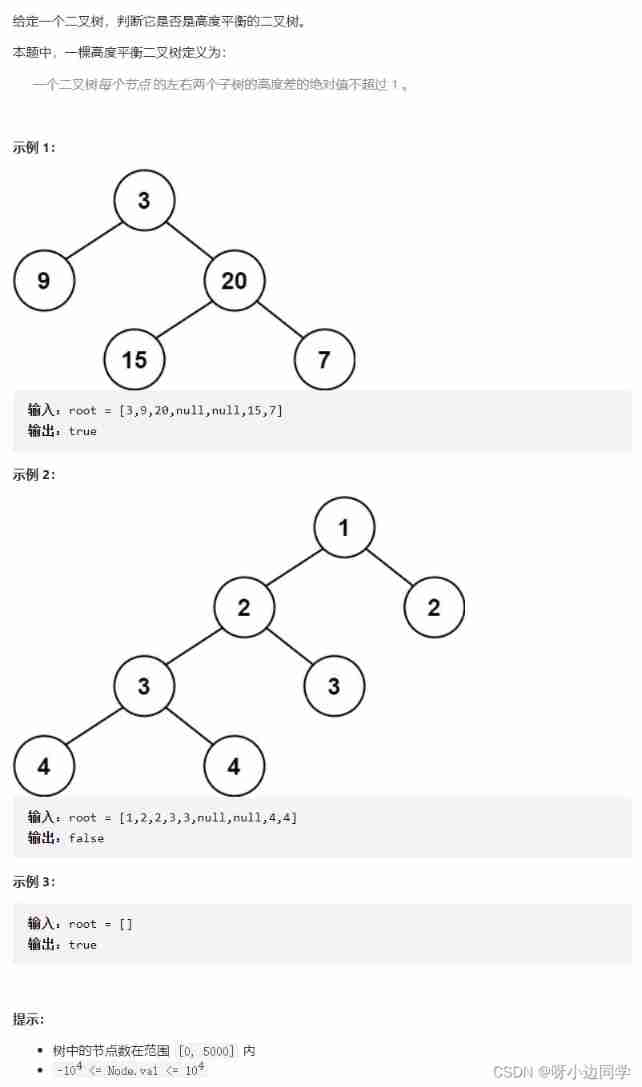
6.2 Ideas and Solutions
Divide and conquer : The top-down
int TreeDepth(struct TreeNode* root)
{
if(root == NULL)
return 0;
int leftDepth = TreeDepth(root->left);
int rightDepth = TreeDepth(root->right);
return 1 + (leftDepth > rightDepth ? leftDepth:rightDepth);
}
bool isBalanced(struct TreeNode* root){
if(root == NULL)
return true;
int gap = abs(TreeDepth(root->left)-TreeDepth(root->right));
if(gap > 1)
return false;
return isBalanced(root->left) && isBalanced(root->right);
}
Time complexity analysis O ( N 2 ) O(N^2) O(N2)
The time complexity of recursion = Number of recursions * Number of recursive calls
- Number of recursions :
isBalanceIn the worst case, traverse all nodes N N N - Number of calls in recursion : Find the height of the tree
TreeDepthThe worst , The tree degenerates into a chain structure N N N
Optimize : Subsequent judgment - Bottom up
Time complexity : O ( N ) O(N) O(N)
bool _isBalanced(struct TreeNode* root, int* ph)
{
if (root == NULL)
{
*ph = 0;// The return height of the empty tree is 0
return true;
}
// Judge the left subtree first , Then judge the right subtree
int leftHight = 0;
if (_isBalanced(root->left, &leftHight) == false)
return false;
int rightHight = 0;
if (_isBalanced(root->right, &rightHight) == false)
return false;
// Bring the height of the current tree to the father on the next level
*ph = fmax(leftHight, rightHight) + 1;
return abs(leftHight - rightHight) < 2;// The condition of balanced binary tree
}
bool isBalanced(struct TreeNode* root)
{
int hight = 0;
return _isBalanced(root, &hight);
}
7. First, middle and last traversal of binary tree
Topic link : Preorder traversal of two tree
Topic link : Middle order traversal of binary trees
Topic link : Postorder traversal of binary trees
There is a little change between the preface here and what we wrote ourselves , So just take it out . Mainly talk about the preface , The middle order and the second order are the same .
It requires that the preorder traversal be stored in the array , An array is malloc To the .
Be careful :
- Output type parameters :Leetcode To return an array , I don't know how big the array is , Multiple return values are not allowed . Send you the address of a variable outside , Dereference assignment , Let the outside get
- How large is the array ? Calculate the number of nodes , Directly open it at one time .
- The interface it gives cannot recurse ( Do you open an array every time ?), Write one yourself Subfunctions ( Add one in front _ Is the naming habit )
- In recursion , Be careful , Right The same
i++. In the last article , When talking about finding the number of nodes in the tree , I have emphasized this problem .
/** * Note: The returned array must be malloced, assume caller calls free(). */
int TreeSize(struct TreeNode* root)
{
if(root == 0)
return 0;
return 1 + TreeSize(root->left) + TreeSize(root->right);
}
void _preorderTraversal(struct TreeNode* root,int* a,int* pi){
if(root == NULL)
return ;
// Put the array in sequence a in
a[*pi] = root-> val;
(*pi)++;
_preorderTraversal(root->left, a, pi);
_preorderTraversal(root->right, a, pi);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize){
int size = TreeSize(root);
*returnSize = size;
int* a = (int*)malloc(size*sizeof(int));
int i = 0;
_preorderTraversal(root, a, &i);
return a;
}
Middle preface & The following sequence should pay attention to the same problems .
In the sequence traversal ——
/** * Note: The returned array must be malloced, assume caller calls free(). */
int TreeSize(struct TreeNode* root)
{
if(root == NULL)
return 0;
return 1 + TreeSize(root->left) + TreeSize(root->right);
}
void _inorderTraversal(struct TreeNode* root, int* a,int* pi)
{
if(root == NULL)
return ;
_inorderTraversal(root->left, a, pi);
a[*pi] = root->val;
(*pi)++;
_inorderTraversal(root->right, a, pi);
}
int* inorderTraversal(struct TreeNode* root, int* returnSize){
int size = TreeSize(root);
*returnSize = size;
int* a = (int*)malloc(size*sizeof(int));
int i = 0;
_inorderTraversal(root, a, &i);
return a;
}
After the sequence traversal ——
int TreeSize(struct TreeNode* root)
{
if(root == NULL)
return NULL;
return 1 + TreeSize(root->left) + TreeSize(root->right);
}
void _postorderTraversal(struct TreeNode* root, int* a,int* pi)
{
if(root == NULL)
return ;
_postorderTraversal(root->left, a, pi);
_postorderTraversal(root->right, a, pi);
a[*pi] = root->val;
(*pi)++;
}
int* postorderTraversal(struct TreeNode* root, int* returnSize){
int size = TreeSize(root);
*returnSize = size;
int* a = (int*)malloc(size*sizeof(int));
int i = 0;
_postorderTraversal(root, a, &i);
return a;
}
8. Construction and traversal of binary tree THU
8.1 subject
Topic link : Construction and traversal of binary tree TsingHua

8.2 Ideas and Solutions
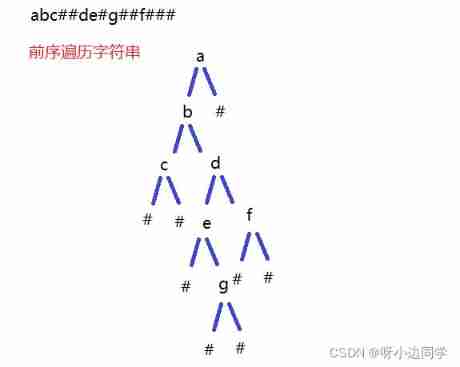
- Pre order traversal string , Building a binary tree recursively
- Medium order printout
- Subsequent destruction
The front, middle and back are all in order , That's wonderful !
notes : When building a binary tree , Traversing the string still uses output parameters , I should be familiar with . The constructed tree is brought back by the return value , There is no need to pass the secondary pointer , You see, the interface of many topics is like this , For example, the above flip binary tree .
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
typedef struct TreeNode
{
char val;
struct TreeNode* left;
struct TreeNode* right;
}TreeNode;
TreeNode* CreateTree(char* str,int* pi)
{
if(str[*pi] == '#')
{
(*pi)++;
return NULL;
}
TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));
root->val = str[*pi];
(*pi)++;
root->left = CreateTree(str, pi);
root->right = CreateTree(str, pi);
return root;
}
void inorderTraversal(TreeNode* root)
{
if(root == NULL)
return ;
inorderTraversal(root->left);
printf("%c ",root->val);
inorderTraversal(root->right);
}
void DestroyTree(TreeNode* root)
{
if(root == NULL)
return ;
DestroyTree(root->left);
DestroyTree(root->right);
free(root);
}
int main()
{
char str[100];
scanf("%s",str);
int i = 0;
TreeNode* root = CreateTree(str, &i);
inorderTraversal(root);
DestroyTree(root);
root = NULL;
return 0;
}
边栏推荐
- [network] channel attention network and spatial attention network
- 最高法院,离婚案件判决标准
- Weng Kai C language third week 3.1 punch in
- Postman测试报告
- Unity screen coordinates ugui coordinates world coordinates conversion between three coordinate systems
- A blog to achieve embedded entry
- Codeforces Round #804 (Div. 2)
- Sqlserver query results are not displayed in tabular form. How to modify them
- Redis has four methods for checking big keys, which are necessary for optimization
- Redis 排查大 key 的4種方法,優化必備
猜你喜欢

Visio draws Tai Chi
8. Static file

ISP learning (2)
CADD course learning (8) -- virtual screening of Compound Library
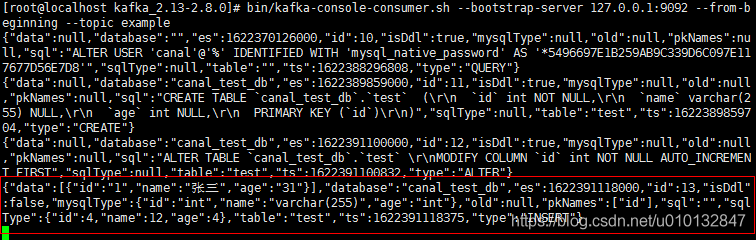
canal同步mysql数据变化到kafka(centos部署)
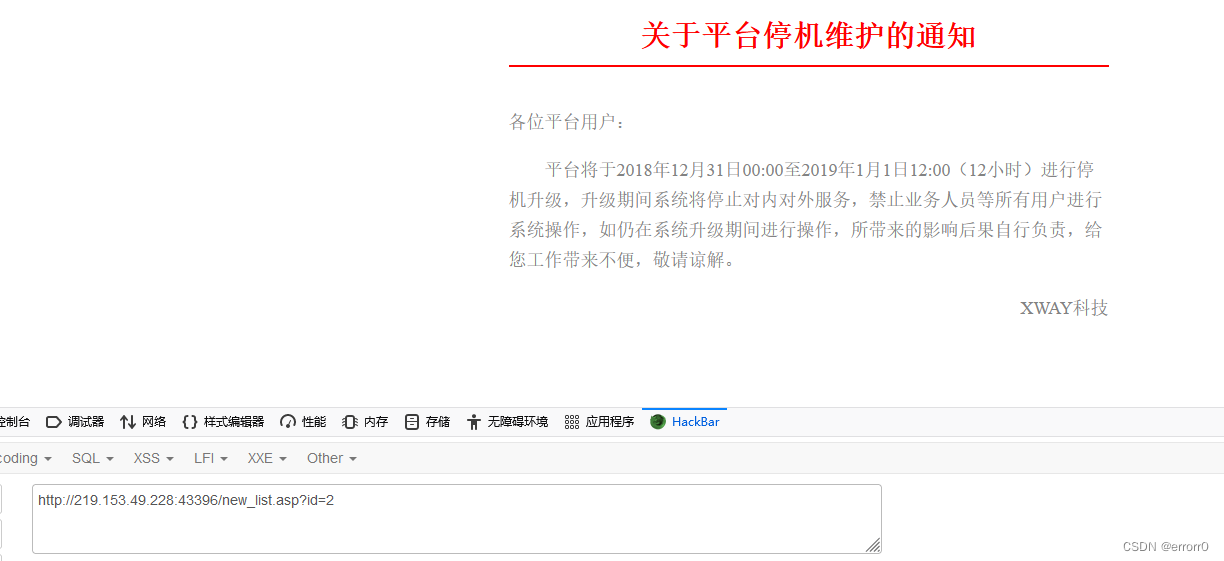
SQL injection vulnerability (MSSQL injection)
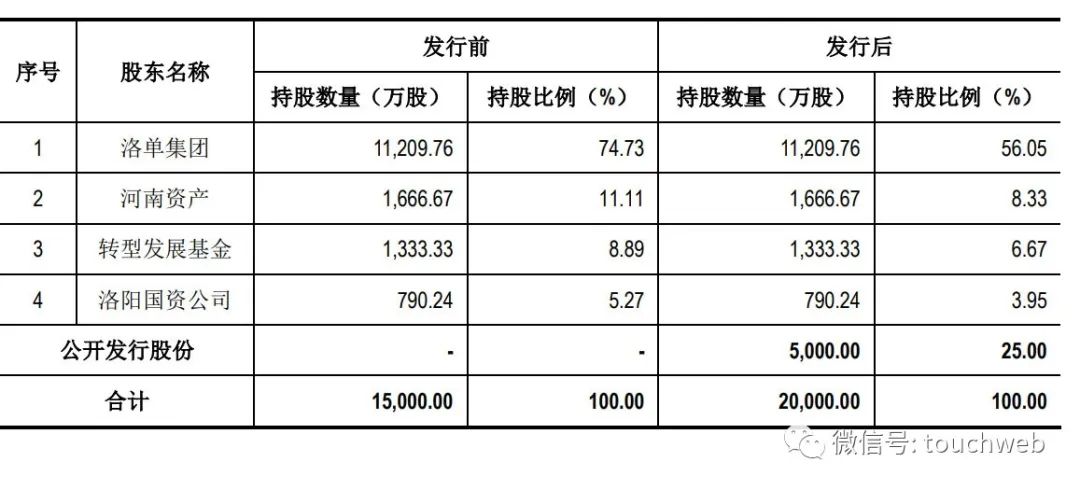
麦斯克电子IPO被终止:曾拟募资8亿 河南资产是股东

The most detailed and comprehensive update content and all functions of guitar pro 8.0
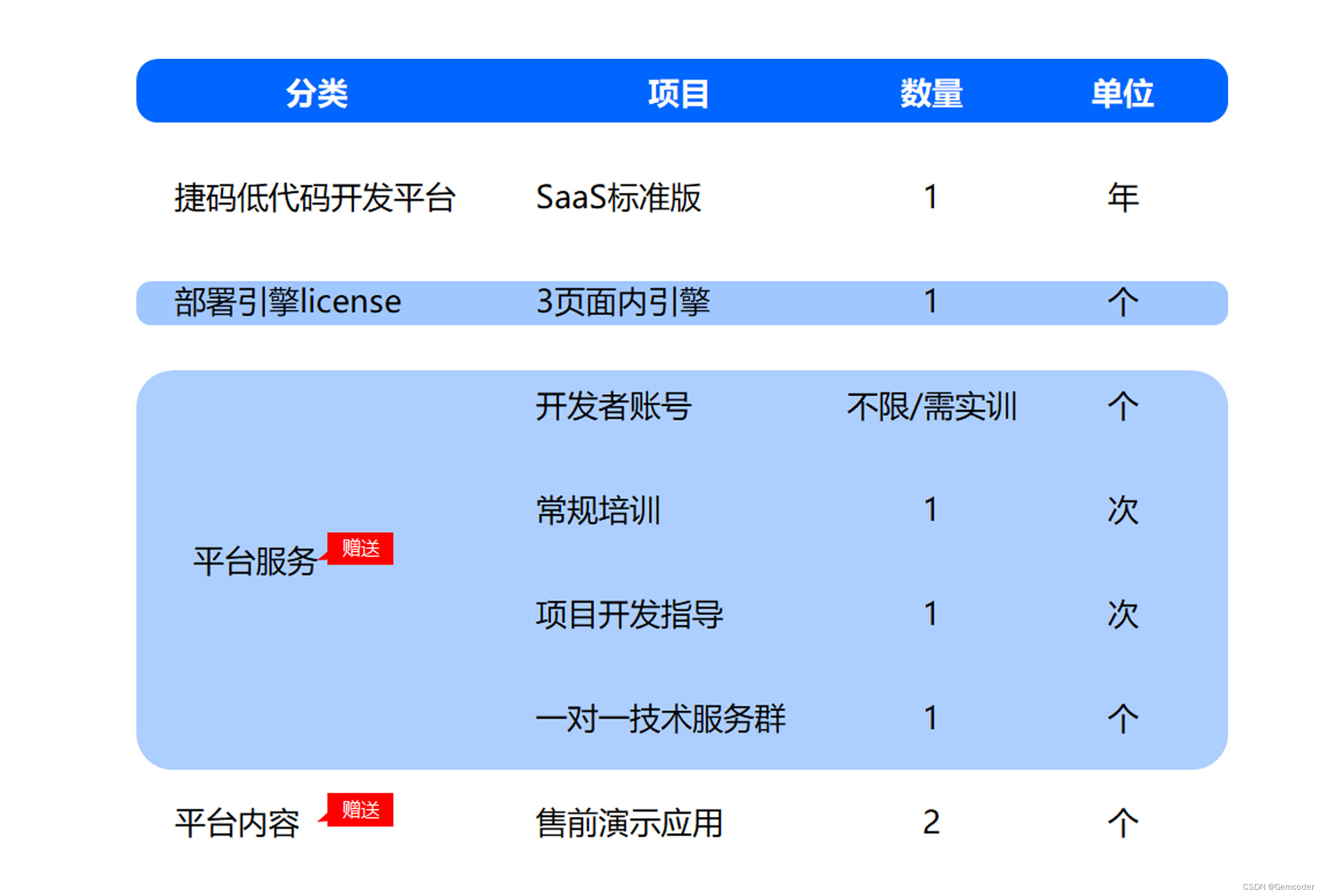
Meet diverse needs: jetmade creates three one-stop development packages to help efficient development

The ECU of 21 Audi q5l 45tfsi brushes is upgraded to master special adjustment, and the horsepower is safely and stably increased to 305 horsepower
随机推荐
[Chongqing Guangdong education] Suzhou University English film and Television Appreciation reference materials
Upload nestjs configuration files, configure the use of middleware and pipelines
Unity screen coordinates ugui coordinates world coordinates conversion between three coordinate systems
Redis —— Redis In Action —— Redis 实战—— 实战篇一 —— 基于 Redis 的短信登录功能 —— Redis + Token 的共享 session 应用— 有代码
Vulnerability discovery - vulnerability probe type utilization and repair of web applications
驱动开发——HelloWDM驱动
[NOIP2009 普及组] 分数线划定
Weng Kai C language third week 3.1 punch in
Distributed transaction solution
Digital children < daily question> (Digital DP)
CADD course learning (8) -- virtual screening of Compound Library
Bubble sort
Etcd database source code analysis -- etcdserver bootstrap initialization storage
SQL注入漏洞(MSSQL注入)
Dynamic programming (tree DP)
2021 robocom world robot developer competition - undergraduate group (semi-finals)
[HBZ share] reasons for slow addition and deletion of ArrayList and fast query
I'd like to ask about the current MySQL CDC design. In the full volume phase, if a chunk's binlog backfill phase,
flink sql 能同时读多个topic吗。with里怎么写
饼干(考试版)