Wu Enda's machine learning after class exercises - linear regression

Univariate linear regression

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

path = "ex1data1.txt"
data = pd.read_csv(path, header=None, names=['Population', 'Profit'])
# pandas.read_csv By default, the first row of the data content will be defaulted to the field name Title ,header=None Indicates that the read raw file data has no column index 
data.head() #  Method is used to return the first... Of a data frame or sequence n That's ok ( The default value is 5). Return type ：DataFrame, It can be understood as a table , Or matrix 
# DataFrame It is essentially a two-dimensional matrix , The difference from the conventional two-dimensional matrix is that the former additionally specifies the names of each row and column .

	Population	Profit
0	6.1101	17.5920
1	5.5277	9.1302
2	8.5186	13.6620
3	7.0032	11.8540
4	5.8598	6.8233

data.describe()
# describe()  Function can view the basic situation of data ,
#  Include ：count  Non null number 、mean  Average 、std  Standard deviation 、max  Maximum 、min  minimum value 、（25%、50%、75%） Quantiles, etc. .

	Population	Profit
count	97.000000	97.000000
mean	8.159800	5.839135
std	3.869884	5.510262
min	5.026900	-2.680700
25%	5.707700	1.986900
50%	6.589400	4.562300
75%	8.578100	7.046700
max	22.203000	24.147000

#  Draw a picture 
data.plot(kind='scatter',x='Population',y='Profit',figsize=(12,8))
# scatter Represents a scatter plot ,figsize Show the size of the picture , Company ： Inch 
plt.show()

​

​

Use gradient descent to minimize the cost function ,
Create a parameter to θ Is the cost function of the characteristic function
$$J\left(\theta \right)=\frac{1}{2m}\sum _{i=1}^m{\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)}^2$$
among ：
$$h_{\theta }\left(x\right)={\theta }^{T}X={\theta }_0{x}_0+{\theta }_1{x}_1+{\theta }_2{x}_2+...+{\theta }_n{x}_n$$

def computeCost(X,y,theta): #  Input X Is a column vector ,y It's also a column vector ,theta It's a line vector 
    inner = np.power(((X*theta.T)-y),2) # x*θ The transpose of is a hypothetical function  power Function calculation numpy The specified power of each value in the array 
    return np.sum(inner/(2*len(X))) #  Will array / All the elements in the matrix add up  len(X) Number of matrix lines 

data.insert(0,'Ones',1)  
#  Insert a column as 1 For better vectorization , You need to add a column to the training set x_0, So that we can use the vectorized solution to calculate the cost and gradient , See video p18

#  Initialization of a variable 
cols = data.shape[1] # shape[0] It's the number of lines  shape[1] It's the number of columns 
X = data.iloc[:,0:cols-1] #  Data sets   All right   List from 0 To cols-1( barring )  Left closed right away 
y = data.iloc[:,cols-1:cols] #  The target 
X.head()

	Ones	Population
0	1	6.1101
1	1	5.5277
2	1	8.5186
3	1	7.0032
4	1	5.8598

The data type obtained is DataFrame type , So you need to do type conversion . Initialization is also required theta, namely theta All elements are set to 0

X = np.matrix(X.values)
y = np.matrix(y.values)
theta = np.matrix(np.array([0,0]))

dimension

X.shape, theta.shape, y.shape

((97, 2), (1, 2), (97, 1))

computeCost(X,y,theta) # Computational cost function 

32.072733877455676

batch gradient decent（ Batch gradient descent ）

$${\theta }_j:={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}J\left(\theta \right)$$
gradient descent

def gradientDescent(X,y,theta,alpha,iters): # iters Is the number of iterations  alpha It's the learning rate   That is, step length 
    temp_theta = np.matrix(np.zeros(theta.shape)) #  Zero value matrix   The staging theta
    parameters = int(theta.ravel().shape[1]) # ravel Calculate the number of parameters to be solved   Function reduces multidimensional array to one dimension   The value here is 2
    cost = np.zeros(iters) # structure iters individual 0 Array of 
    # iteration ：
    for i in range(iters):
        difference = (X*theta.T) - y #  Difference value 
        for j in range(parameters):
            term = np.multiply(difference,X[:,j])    # multiply x_i X[:,j] Represents all lines  j Column , In short, draw out the number j Column  
             #  Note that this is not matrix multiplication   Here is the multiplication after derivation  multiply Is the number of corresponding positions of two matrices of the same size multiplied directly 
            temp_theta[0,j] = theta[0,j] - (alpha/len(X))*np.sum(term) #  to update theta_j
        
        theta = temp_theta #  Update all theta value 
        cost[i] = computeCost(X,y,theta) #  Renewal value 
    
    return theta,cost

Initialize some additional variables - Learning rate α And the number of iterations to perform .

alpha = 0.01
iters = 1000

obtain theta value , Minimum cost

g,cost = gradientDescent(X,y,theta,alpha,iters)
g

matrix([[-3.24140214,  1.1272942 ]])

cost[-1] #  Get the last value of the array 

4.515955503078913

Last , Use what we fitted theta Value calculation of the cost function of the training model

computeCost(X, y, g)

4.515955503078913

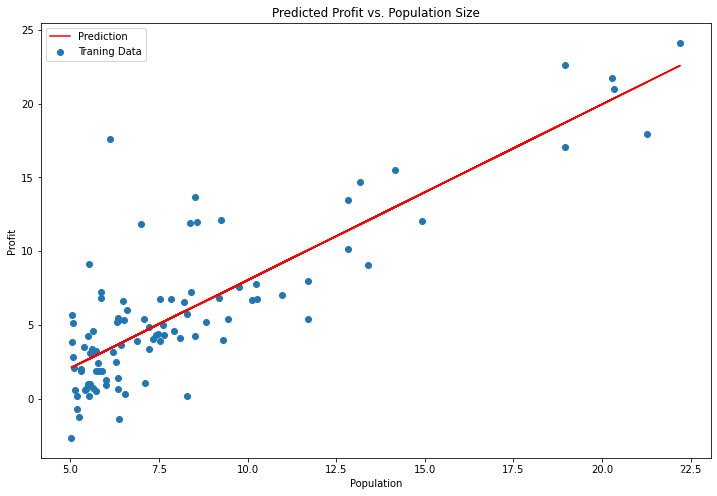
Draw linear models and data , Intuitively see its fitting

x = np.linspace(data.Population.min(), data.Population.max(), 100) #  Generates a one-dimensional array of the specified number within the specified range 
f = g[0, 0] + (g[0, 1] * x) # x1=1 g[0, 0] Express theta_0 g[0, 1] Express theta_1

fig, ax = plt.subplots(figsize=(12,8)) # plt.subplot() Function is used to directly specify the division method and position for drawing .
# fig Represents the drawing window (Figure);ax Represents the coordinate system on this drawing window (axis), Will generally continue to ax To operate .

#  Function to set the abscissa and ordinate , And set the color to red , Mark... On the icon 'Prediction' label   Abscissa x  Ordinate f
ax.plot(x, f, 'r', label='Prediction') 
#  Define the abscissa and ordinate of the scatter chart , The of scatter plot points is given 'Traning Data' Tag name 
ax.scatter(data.Population, data.Profit, label='Traning Data') 
ax.legend(loc=2)  # 2 In the upper left corner 


ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs. Population Size')
plt.show()

​

​

Since the gradient equation function also outputs a cost vector in each training iteration , So we can also draw . Be careful , The cost is always lower

fig, ax = plt.subplots(figsize=(12,8))
ax.plot(np.arange(iters), cost, 'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
plt.show()

​

​

Multivariate linear regression

This exercise includes a housing price data set , It contains two variables （ The size of the house 、 Number of bedrooms ） And the target （ House price ）.

path =  'ex1data2.txt'
data2 = pd.read_csv(path, header=None, names=['Size', 'Bedrooms', 'Price'])
data2.head()

	Size	Bedrooms	Price
0	2104	3	399900
1	1600	3	329900
2	2400	3	369000
3	1416	2	232000
4	3000	4	539900

data2.describe()

	Size	Bedrooms	Price
count	47.000000	47.000000	47.000000
mean	2000.680851	3.170213	340412.659574
std	794.702354	0.760982	125039.899586
min	852.000000	1.000000	169900.000000
25%	1432.000000	3.000000	249900.000000
50%	1888.000000	3.000000	299900.000000
75%	2269.000000	4.000000	384450.000000
max	4478.000000	5.000000	699900.000000

The house is about the size of the number of bedrooms 1000 times . When features differ by several orders of magnitude , First perform feature scaling （ Mean normalization ） It can make the gradient descent converge faster .

data2 = (data2 - data2.mean()) / data2.std() #  The solution is to try to scale all feature scales to  -1 ~ 1
data2.head()

	Size	Bedrooms	Price
0	0.130010	-0.223675	0.475747
1	-0.504190	-0.223675	-0.084074
2	0.502476	-0.223675	0.228626
3	-0.735723	-1.537767	-0.867025
4	1.257476	1.090417	1.595389

data2.insert(0, 'Ones', 1) 
cols = data2.shape[1]
X2 = data2.iloc[:,0:cols-1]
y2 = data2.iloc[:,cols-1:cols]

X2 = np.matrix(X2.values)
y2 = np.matrix(y2.values)
theta2 = np.matrix(np.array([0,0,0]))

g2, cost2 = gradientDescent(X2, y2, theta2, alpha, iters)
computeCost(X2, y2, g2) #  Calculate the cost 

0.1307033696077189

Cost function convergence graph

fig, ax = plt.subplots(figsize=(12,8))
ax.plot(np.arange(iters), cost2, 'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
plt.show()

​

​

Use sklearn Linear regression function simplification process

from sklearn import linear_model
model = linear_model.LinearRegression()  # Linear regression based on least square method .
model.fit(X, y)

x = np.array(X[:, 1].A1)
f = model.predict(X).flatten()

fig, ax = plt.subplots(figsize=(12,8))
ax.plot(x, f, 'r', label='Prediction')
ax.scatter(data.Population, data.Profit, label='Traning Data')
ax.legend(loc=2)
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs. Population Size')
plt.show()

normal equation（ Normal equation ）

Ideas

The normal equation is to find the parameters that minimize the cost function by solving the following equation ：$\frac{\partial }{\partial {\theta }_j}J\left({\theta }_j\right)=0$ .
Suppose that the characteristic matrix of our training set is X（ Contains $x_0=1$） And the result of our training set is vector y, Then use the normal equation to solve the vector $\theta ={\left(X^{T}X\right)}^{-1}{X}^{T}y$ .
Superscript T Transposition of representative matrix , Superscript -1 Represents the inverse of a matrix . Let's set the matrix $A=X^{T}X$, be ：${\left(X^{T}X\right)}^{-1}=A^{-1}$

Gradient descent versus normal equation ：

gradient descent ： We need to choose the learning rate α, It takes several iterations , When the number of features n It can also be better applied when it is large , It's suitable for all kinds of models
Normal equation ： There is no need to choose the learning rate α, Calculated at one time , Need to compute ${\left(X^{T}X\right)}^{-1}$, If the number of features n If it's bigger, it's more expensive , Because the computation time complexity of matrix inverse is $O(n3)$, Generally speaking, when $n$ Less than 10000 It's still acceptable , Only for linear models , It is not suitable for other models such as logistic regression model

#  Normal equation function 
def normalEqn(X, y):
    theta = np.linalg.inv(X.[email protected])@X.[email protected]#[email protected] Equivalent to X.T.dot(X) np.linalg.inv()： Matrix inversion 
    return theta

final_theta2=normalEqn(X, y)
final_theta2  #  gradient matrix([[-3.24140214, 1.1272942 ]])

matrix([[-3.89578088],
        [ 1.19303364]])