当前位置:网站首页>[leetcode] 450 and 98 (deletion and verification of binary search tree)
[leetcode] 450 and 98 (deletion and verification of binary search tree)
2022-07-07 03:33:00 【Learn a little every day】
Search and insert of binary search tree The second part is the deletion and verification of binary search tree
This paper introduces how to use the characteristics of binary search tree to realize 「 Delete 」 and 「 verification 」 operation .
450. Delete nodes in binary search tree
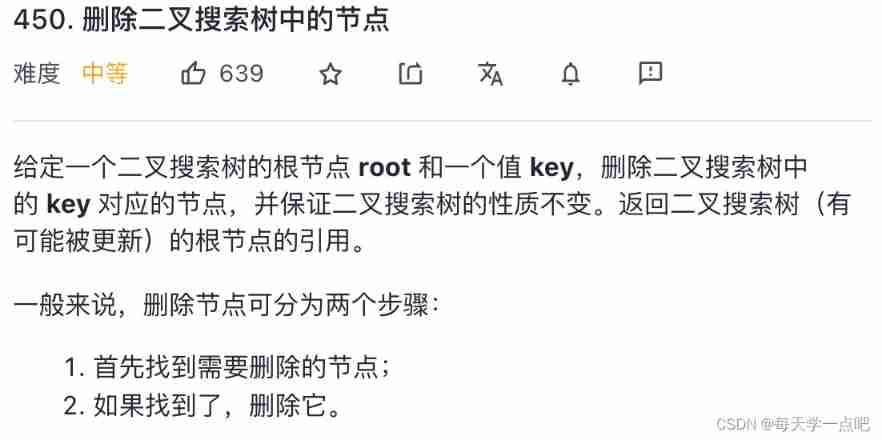
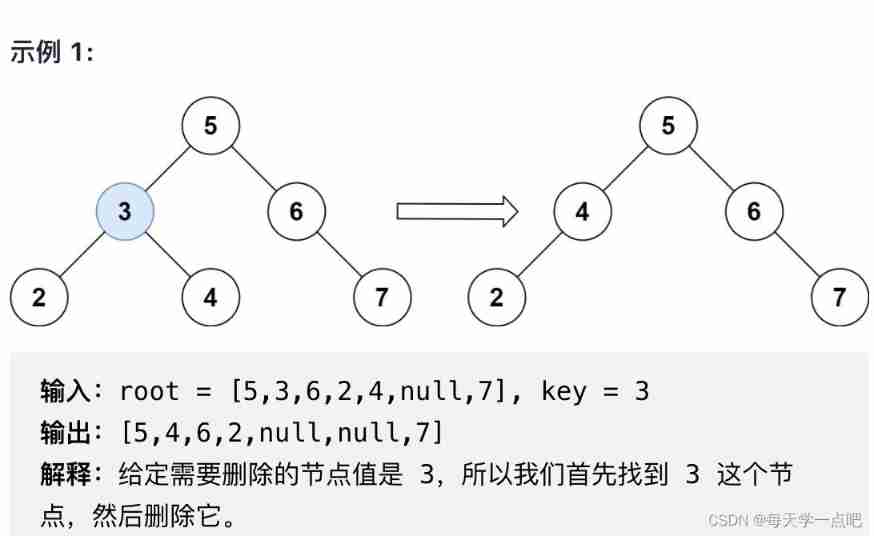
solution : recursive
Different from the deletion of ordinary binary tree , The binary search tree should adjust the tree nodes after deleting the corresponding nodes , Restore binary search tree . There are three cases of deleting nodes :
- The left subtree is empty . The root node of the right subtree replaces the current node .
- Left subtree is not empty , The right subtree is empty . The root node of the left subtree replaces the current node .
- The left and right subtrees are not empty . Use the right subtree minimum node ( Leftmost son ) To replace , And delete the minimum node .
class Solution:
def deleteNode(self, root: Optional[TreeNode], key: int) -> Optional[TreeNode]:
if not root:
return None
if root.val == key:
# situation 1
if not root.left:
return root.right
# situation 2
if not root.right:
return root.left
# situation 3
# Find the smallest node of the right subtree
minNode = self.getMin(root.right)
# Delete the smallest node from the right subtree
root.right = self.deleteNode(root.right, minNode.val)
# Replace the current node , Complete the delete operation
root.val = minNode.val
elif root.val > key:
# Enter the left subtree to search
root.left = self.deleteNode(root.left, key)
else:
# Enter the right subtree to search
root.right = self.deleteNode(root.right, key)
return root
# Find the minimum node of the right subtree
def getMin(self, node):
while node.left:
node = node.left
return node
98. Verify binary search tree
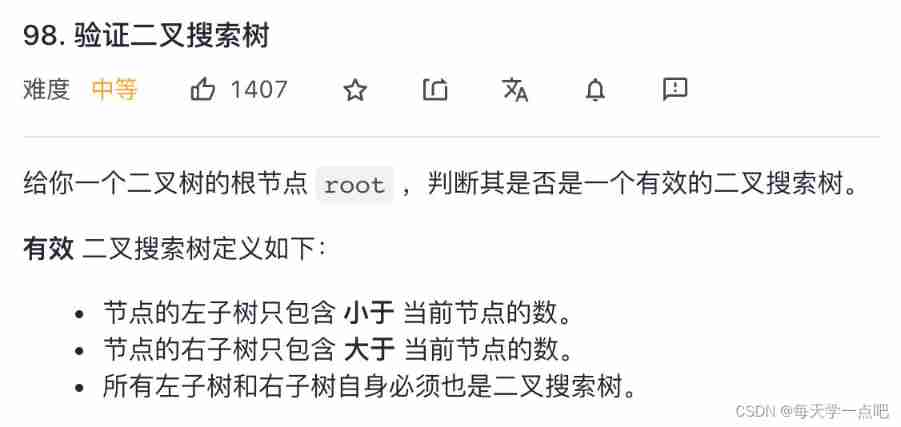
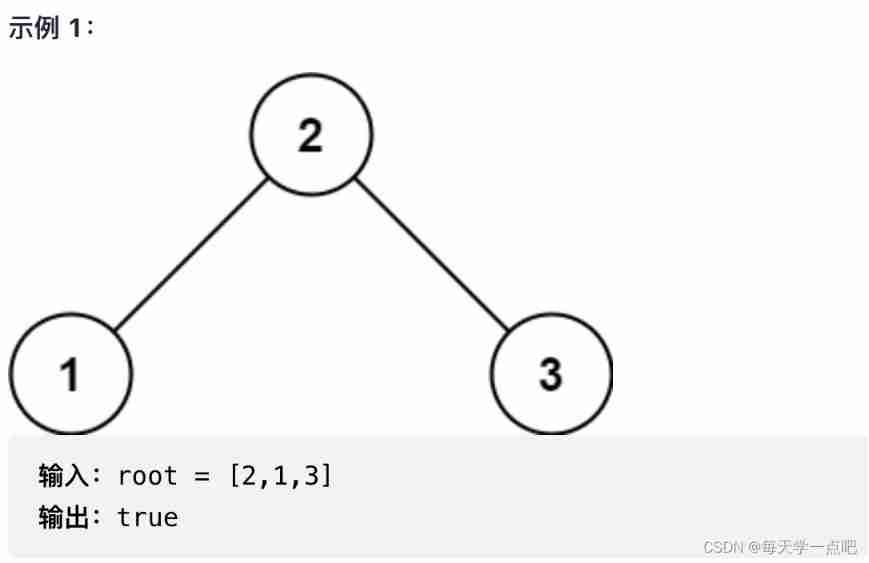
solution : In the sequence traversal
Binary search tree (BST) The middle order traversal of is an ordered result , This can be used to determine whether the current tree is a correct binary search tree . The specific performance is to maintain a variable to store the previous calendar value , Judge whether the current node value is greater than the traversal , If more than , Update variable information , Otherwise return to False, Indicates that the subtree of the current node is not a binary search tree .
In the root The node is a subtree of the root node , The determination process of whether it is a binary search tree is as follows ( Any node 「 What to do 」:
- First determine whether the left subtree is a binary search tree .
- Determine whether the right subtree is a binary search tree .
- Judge whether the current element meets BST nature
- If the above conditions are met , with root The subtree with borrowing as the root node is a binary search tree , return True.
class Solution:
def isValidBST(self, root: TreeNode) -> bool:
maxValue = float("-inf")
def traversal(root):
nonlocal maxValue
if not root:
return True
# Determine whether the left subtree is BST
left = traversal(root.left)
if root.val <= maxValue:
return False
maxValue = root.val
# Judge whether the right subtree is BST
right = traversal(root.right)
# All for True, Indicates that root The subtree with borrowing as the root node is BST.
return left and right
return traversal(root)
summary
1、 If the current node will be down ⾯ Of ⼦ Nodes have an overall impact , You can add ⻓ parameter list , Passing information by means of parameters .
2、 stay ⼆ Fork tree recursion framework , Extended out ⼀ set BST The code framework :
3. According to the code framework BST Add, delete, check and modify .
边栏推荐
- 23.(arcgis api for js篇)arcgis api for js椭圆采集(SketchViewModel)
- [cpk-ra6m4 development board environment construction based on RT thread studio]
- VHDL实现任意大小矩阵乘法运算
- 树莓派设置静态ip
- 装饰设计企业网站管理系统源码(含手机版源码)
- Matlab Error (Matrix dimensions must agree)
- 图形化工具打包YOLOv5,生成可执行文件EXE
- CMB's written test - quantitative relationship
- 21. (article ArcGIS API for JS) ArcGIS API for JS rectangular acquisition (sketchviewmodel)
- 树莓派设置wifi自动连接
猜你喜欢
![Jericho turns on the display icon of the classic Bluetooth hid mobile phone to set the keyboard [chapter]](/img/f4/8464bf9b66a1215265ac873f286688.png)
Jericho turns on the display icon of the classic Bluetooth hid mobile phone to set the keyboard [chapter]

体会设计细节

20. (ArcGIS API for JS) ArcGIS API for JS surface collection (sketchviewmodel)
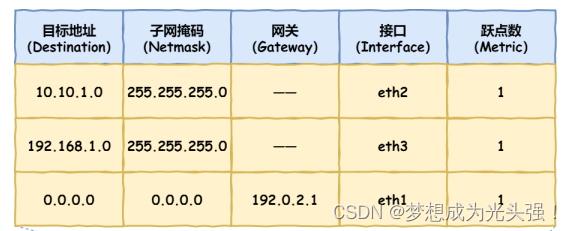
我的勇敢对线之路--详细阐述,浏览器输入URL发生了什么

21. (article ArcGIS API for JS) ArcGIS API for JS rectangular acquisition (sketchviewmodel)
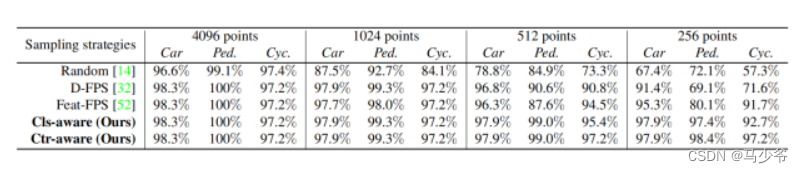
Not All Points Are Equal Learning Highly Efficient Point-based Detectors for 3D LiDAR Point
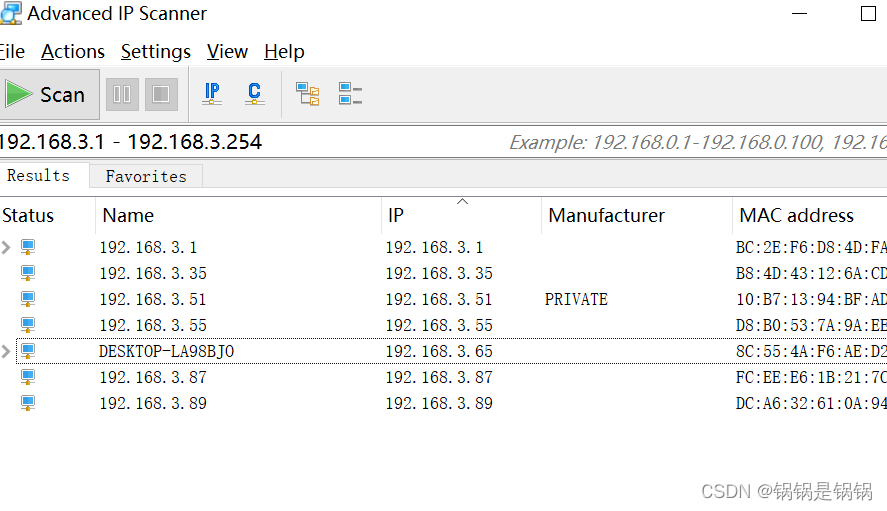
Set WiFi automatic connection for raspberry pie
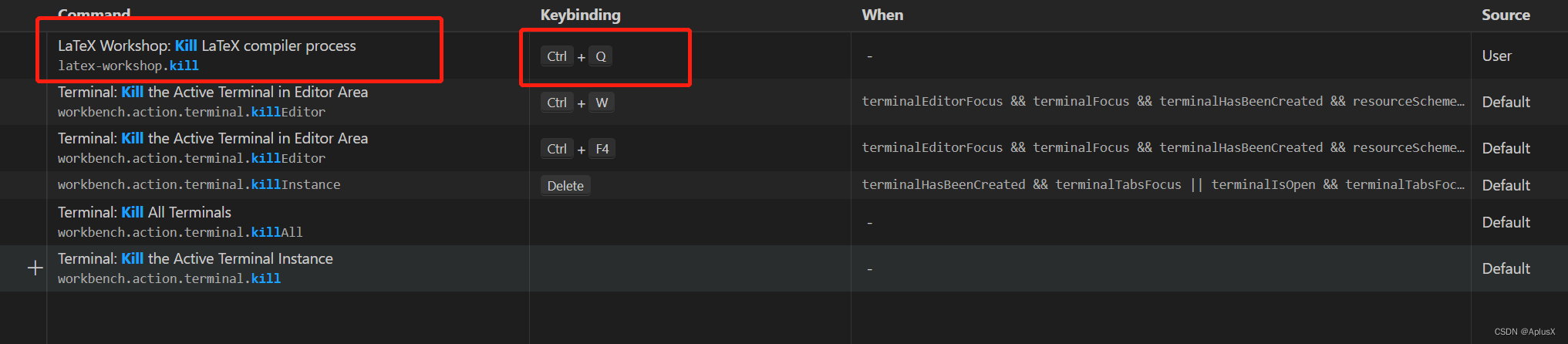
如何自定义Latex停止运行的快捷键
ubuntu20安装redisjson记录
![[safe office and productivity application] Shanghai daoning provides you with onlyoffice download, trial and tutorial](/img/58/d869939157669891f369fb274d32af.jpg)
[safe office and productivity application] Shanghai daoning provides you with onlyoffice download, trial and tutorial
随机推荐
Jericho is in non Bluetooth mode. Do not jump back to Bluetooth mode when connecting the mobile phone [chapter]
19.(arcgis api for js篇)arcgis api for js线采集(SketchViewModel)
Optimization of application startup speed
Opencv environment, and open a local PC camera.
20.(arcgis api for js篇)arcgis api for js面采集(SketchViewModel)
编译常量、ClassLoader类、系统类加载器深度探析
Not All Points Are Equal Learning Highly Efficient Point-based Detectors for 3D LiDAR Point
SQL中删除数据
Jerry's broadcast has built-in flash prompt tone to control playback pause [chapter]
19. (ArcGIS API for JS) ArcGIS API for JS line acquisition (sketchviewmodel)
About Estimation Statistics
Delete data in SQL
[colmap] 3D reconstruction with known camera pose
HMS core machine learning service creates a new "sound" state of simultaneous interpreting translation, and AI makes international exchanges smoother
Sorting operation partition, argpartition, sort, argsort in numpy
R数据分析:cox模型如何做预测,高分文章复现
【达梦数据库】添加自动收集统计信息的任务
Set static IP for raspberry pie
[dream database] add the task of automatically collecting statistical information
Flink task exit process and failover mechanism