当前位置:网站首页>[weekly pit] positive integer factorization prime factor + [solution] calculate the sum of prime numbers within 100
[weekly pit] positive integer factorization prime factor + [solution] calculate the sum of prime numbers within 100
2022-07-06 20:19:00 【Crossin's programming classroom】
Zero basis python Introductory tutorial :python666.cn
Hello everyone , Welcome to Crossin Programming classroom of !
This week we continue to work with “ Prime number ” screwing .
Please listen to :
Divide a positive integer into prime factors . If it's a prime number , The output “ This is a prime number ”
About Decomposing prime factor : Each sum can be written in the form of multiplication of several prime numbers , Each prime number is a factor of the sum , Express a sum in the form of multiplication of prime factors , It's called the decomposition prime factor . The decomposition prime factor is only for the sum .
for example :
Input 90, Output 2 3 3 5
Input 23, Output This is a prime number
Detailed answers and reference codes will be given in the next column , You can also refer to the code in the message of other students .
I look forward to your answers , I hope you can complete the whole series .
Simple code can be submitted directly in the message , Long code is recommended paste.ubuntu.com or
codeshare.io And other code sharing sites , Just copy the code and save it , You can get a share address , Very convenient .
For past questions, click the collection at the beginning of the article “ Every Monday ” Enter the view .
【 answer 】 Calculation 100 Sum of prime numbers within
The general idea of this question is :
Traverse 2~100:
Judge whether the current number is a prime number
If it's a prime number , Add the value to the result
Output results The basic method of judging prime numbers is :
Traverse 2~ Number to be judged :
Determine whether it can be divided by the current number
If you can divide , Is not a prime number
If there is nothing divisible after traversal , Is a prime number however , There are many places that can be optimized , Let the program get the result with less calculation times . For example, judge a number N Whether prime numbers do not need to be traversed 2~N, Just go to √N that will do .
You can look at the last issue @ A stone The answer to , It is a good optimization scheme :
def primeSum(N=100):
initial=[]
prime=0
node=int(N**0.5)+1
for i in range(2,node):
if 0 not in [i%pr for pr in initial]:
prime+=i
initial.append(i)
for i in range(node,N):
if 0 not in [i%pr for pr in initial]:
prime+=i
return prime
print(primeSum()) I mentioned it last time , Let's talk about an interesting solution . The idea of this solution is contrary to the conventional , It's not to judge who is prime , It's to get rid of those that are not prime numbers :
establish 2~100 A list of L
If the list L There's still value in , Then continue the cycle :
hold L[0] The value of is added to the result
For a list of L The elements in , Can be L[0] Don't divide everything , The rest becomes new L Code :
def primeSum(N=100):
initial = list(range(2,N+1))
prime = 0
while len(initial) > 0:
i = initial[0]
prime += i
initial = [num for num in initial if num % i != 0]
return prime
print(primeSum())The result is 1060
_ Previous articles are recommended _
【 Every Monday 】 Calculation 100 Sum of prime numbers within
If you need to know Paid premium courses And Teaching Q & a service
Please be there. Crossin Programming classroom of Internal reply : 666

边栏推荐
- 腾讯字节阿里小米京东大厂Offer拿到手软,老师讲的真棒
- Unity making plug-ins
- Cesium Click to draw a circle (dynamically draw a circle)
- 新一代垃圾回收器—ZGC
- 永磁同步电机转子位置估算专题 —— 基波模型与转子位置角
- 01 基础入门-概念名词
- Tencent byte Alibaba Xiaomi jd.com offer got a soft hand, and the teacher said it was great
- Unity makes AB package
- RT-Thread 组件 FinSH 使用时遇到的问题
- A5000 vgpu display mode switching
猜你喜欢
OceanBase社区版之OBD方式部署方式单机安装
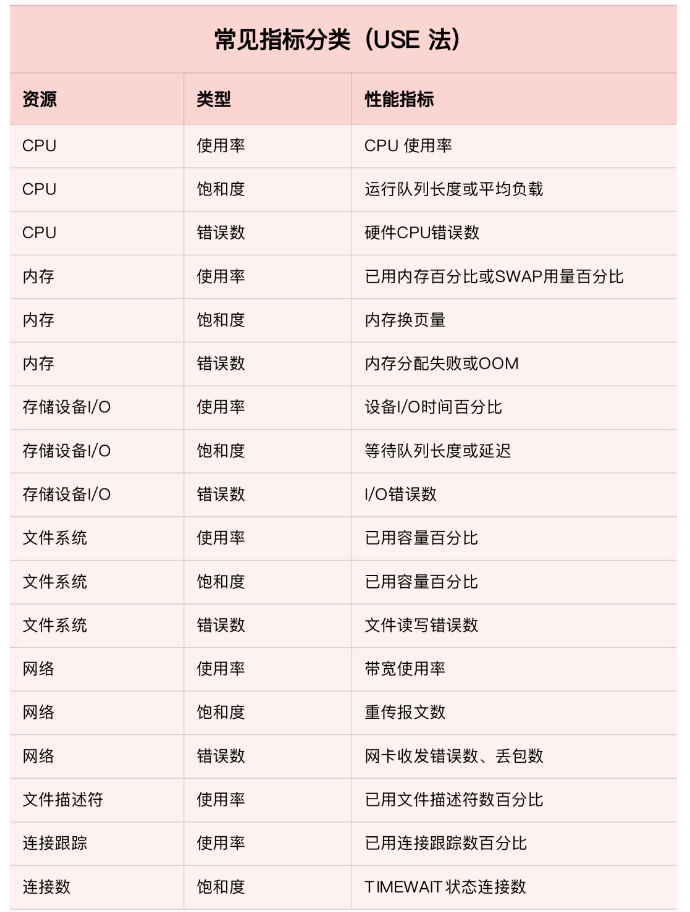
Ideas and methods of system and application monitoring

【每周一坑】信息加密 +【解答】正整数分解质因数

逻辑是个好东西
A5000 vgpu display mode switching

PowerPivot——DAX(初识)
Rhcsa Road
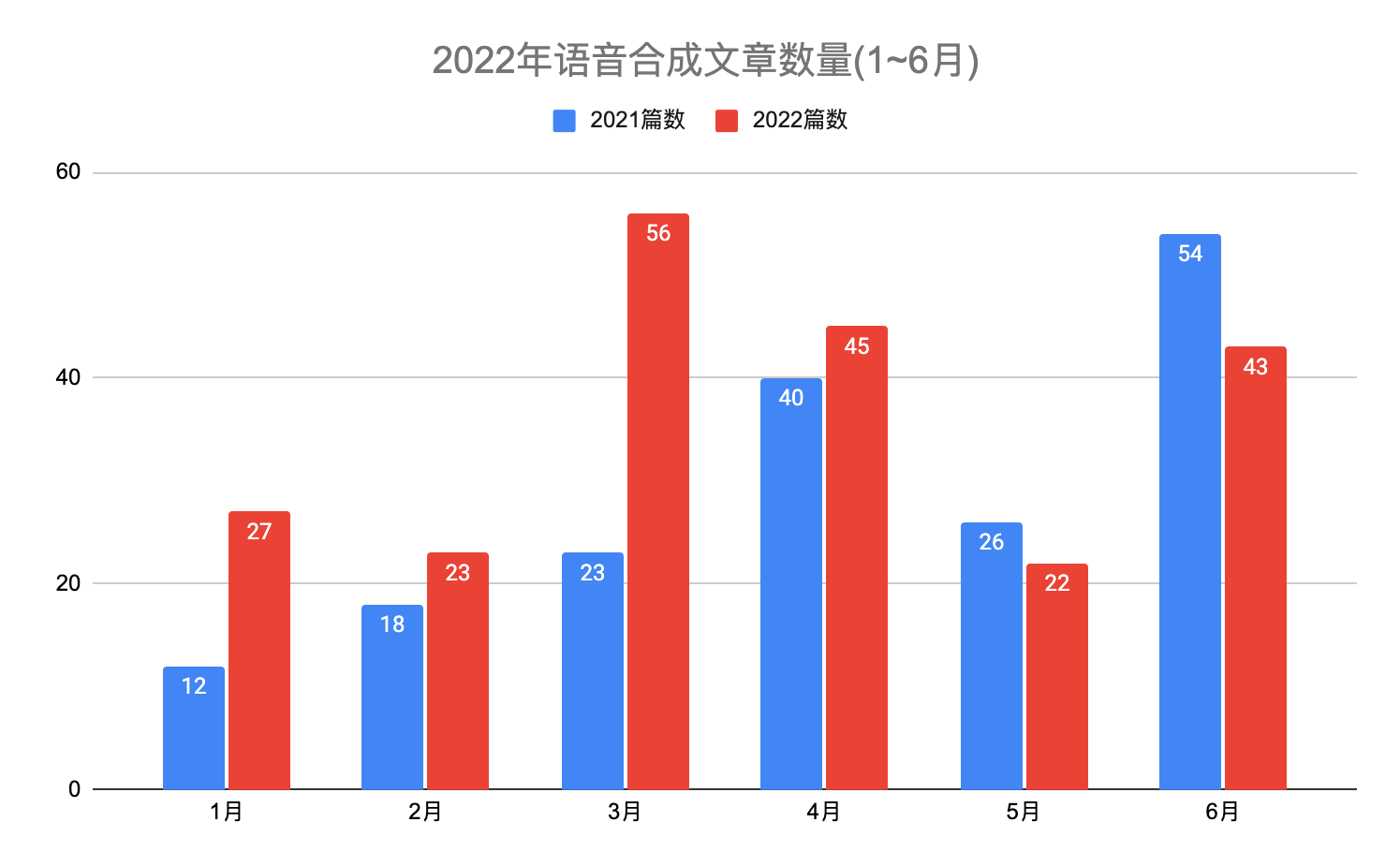
Monthly report of speech synthesis (TTS) and speech recognition (ASR) papers in June 2022
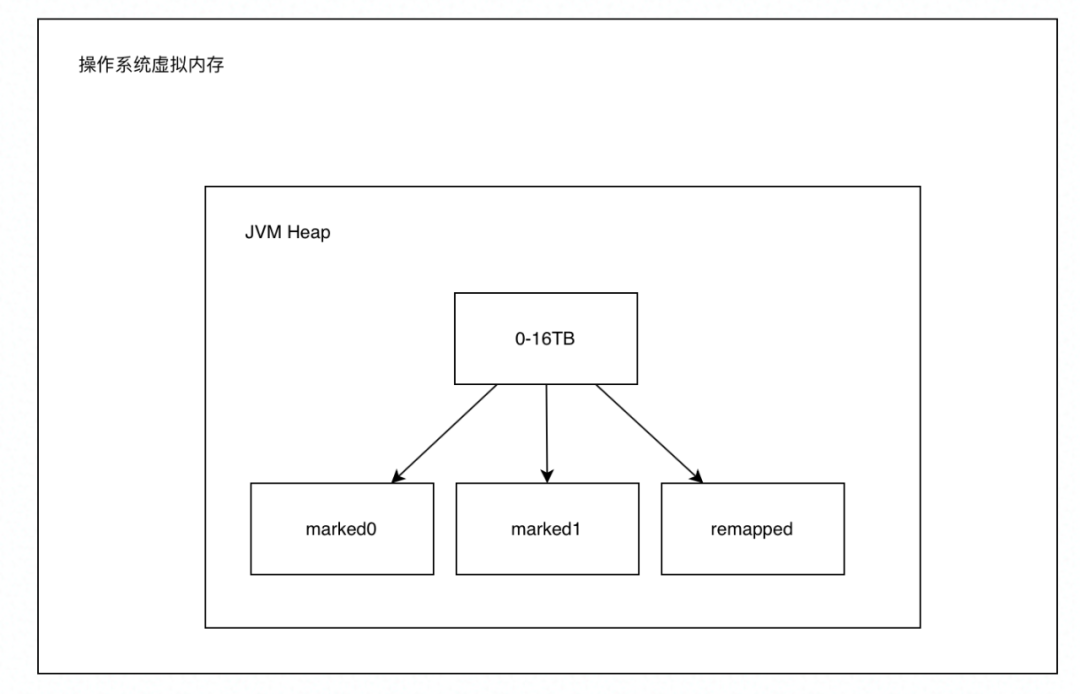
新一代垃圾回收器—ZGC
An East SMS login resurrection installation and deployment tutorial
随机推荐
Notes on beagleboneblack
22-07-05 七牛云存储图片、用户头像上传
Tencent byte and other big companies interview real questions summary, Netease architects in-depth explanation of Android Development
Anaconda安装后Jupyter launch 没反应&网页打开运行没执行
How does kubernetes support stateful applications through statefulset? (07)
How to handle the timeout of golang
AddressSanitizer 技术初体验
腾讯T4架构师,android面试基础
AsyncHandler
新一代垃圾回收器—ZGC
What happened to the kernel after malloc() was transferred? Attached malloc () and free () implementation source
rt-thread i2c 使用教程
Problems encountered in using RT thread component fish
Maximum likelihood estimation and cross entropy loss
Extraction rules and test objectives of performance test points
Introduction of Xia Zhigang
Node. Js: express + MySQL realizes registration, login and identity authentication
电子游戏的核心原理
Guangzhou's first data security summit will open in Baiyun District
Leetcode question 283 Move zero