当前位置:网站首页>2-3查找树
2-3查找树
2022-07-07 05:26:00 【Perkinl】
2-3 查找树(2-3-Search-Tree)
- 2-结点:标准二叉树中的结点称为2-结点(含有一个键和两条链接)。
- 3-结点:包含两个键和三条链接。
定义:一颗2-3查找树或为一棵空树,或由以下结点组成:
2-结点,含有一个键(及其对应的值)和两条链接,左链接指向的2-3树中的键都小于该结点,右链接指向的2-3树中的键都大于该结点。
3-结点,含有两个键(及其对应的值)和三条链接,左链接指向的2-3树中的键都小于该结点,中链接指向的2-3树中的键都位于该结点的 两个键之间,右链接指向的2-3树中的键都大于该结点。
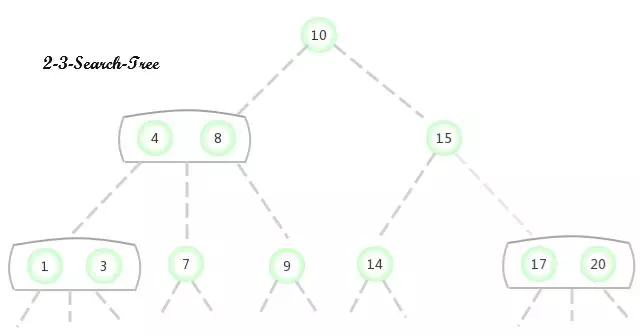
2-3 查找树(2-3-Search-Tree) 操作
一棵完美平衡的2-3查找树中所有空链接到根节点的距离应该都是相同的。
查找
2-3 查找树中的查找与二分搜索树的查找类似。要判断一个键是否在树中,先将它和根结点中的键比较。如果它和其中任意一个 相等,查找命中。否则,根据比较的结果找到指向相应区间的链接,并在其指向的子树中递归继续查找。如果是个空链接,查找未命中。
在如上图所示的2-3树中查找键为2的结点是否存在,过程如下:
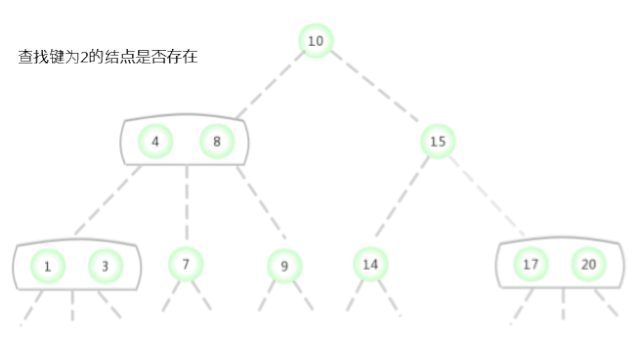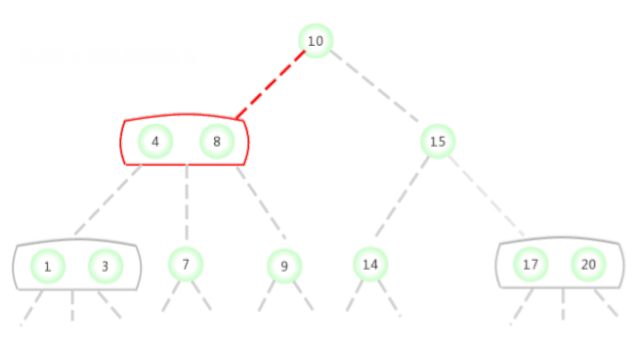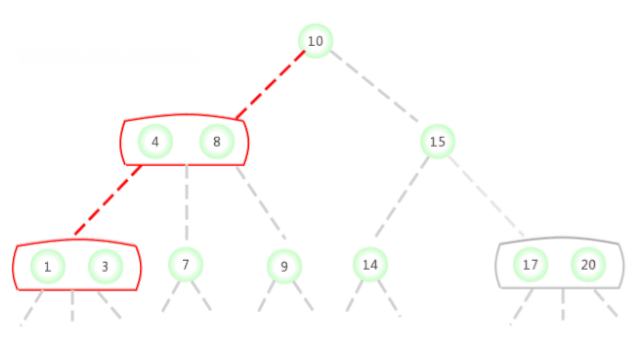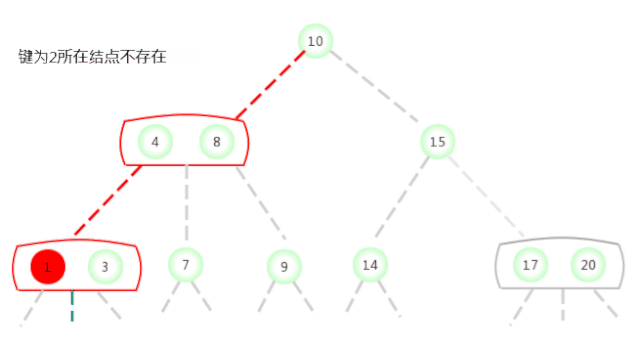
在如上图所示的2-3树中查找键为17的结点是否存在,过程如下:
插入
向2-结点中插入新键
要在2-3树中插入一个新的结点,类似于二分搜索树的插入,先进行一次未命中的查找,找到要插入的结点所在的位置,将其挂在树的底部。 但这样一来树就无法保证完美平衡性。使用2-3的主要原因:在插入新的结点之后能够继续保持平衡。
如果未命中的查找结束于一个2-结点,就将这个2-结点替换为3-结点,将要插入的键保存在其中即可。
如果未命中的查找结束于一个3-结点,分析过程如下。
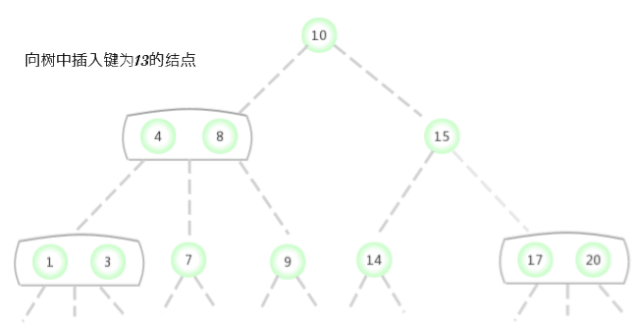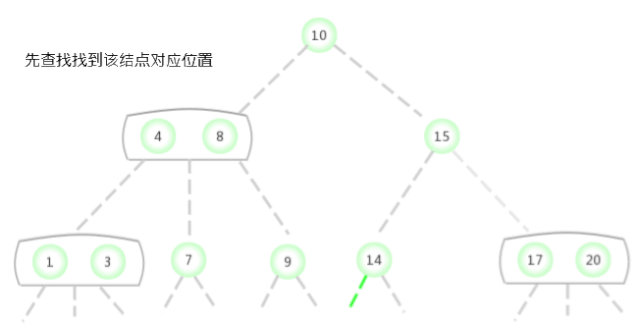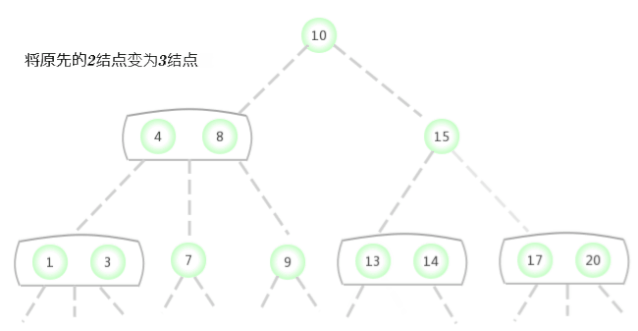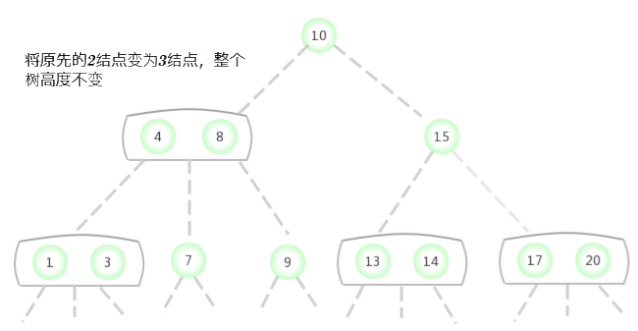
向一棵只含有一个3-结点的树中插入新键
在考虑一般情况之前,先假设我们需要向一棵只含有一个3-结点的树中插入一个新键。这棵树中有两个键,所以在它唯一的结点中 已经没有可插入新键的空间了。为了将新键插入,先临时将新键存入该结点中,形成一个4-结点(含有3个键和4条连接)。创建一个4-结点很方便, 因为很容易将其转化成为一棵由3个2-结点组成的2-3树,其中一个结点(根)含有中键,一个结点含有3个键中的最小者(和根结点的左链接相连), 一个结点含有3个键中的最大者(和根结点的右链接相连)。这棵树即是一棵含有3个结点的二叉查找树,同时也是一棵完美平衡的2-3树,因为其中所有的 空链接到跟结点的距离都相等。插入前树的高度是0,插入后树的高度是1。
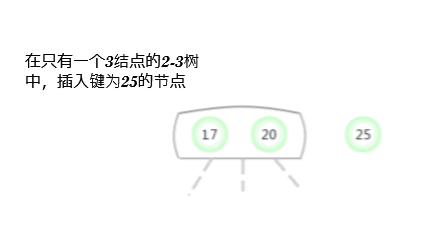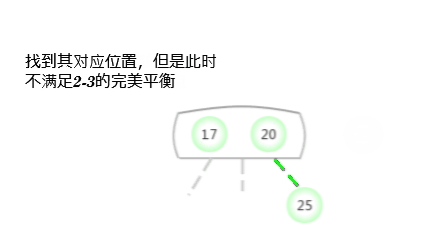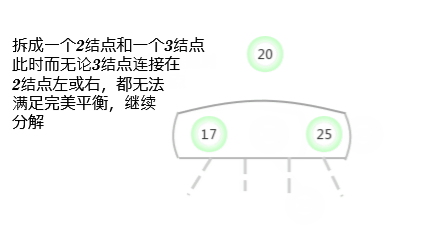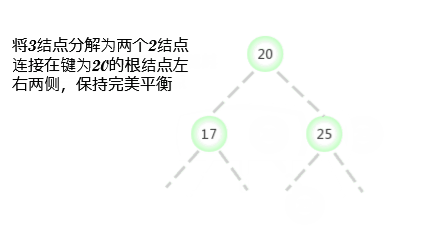
向一个父结点为2-结点的3-结点中插入新键
假设未命中的查找结束于一个3-结点,而它的父结点是一个2-结点。在这种情况下需要:在维持树的完美平衡的前提下为新键 腾出空间。 需要像刚才一样构造一个临时的4-结点并将其分解,但此时不会为中键创建一个新结点,而是将其移动到原来的父结点中。
将这次转换看成将指向原3-结点的一条链接替换为新父结点中的原中键左右两边的两条链接,并分别指向两个新的2-结点。 根据假设,父结点中石油空间的:父结点是一个2-结点,插入之后变成了一个3-结点。另外,这次转换也不影响(完美平衡的)2-3树的 主要性质。树仍然是有序的,因为中键被移到父节点中去了;树仍然是完美平衡的,插入后所有的叶子结点到根结点的距离仍然相同。
上述过程是2-3树动态变化的核心,图示展示如下:
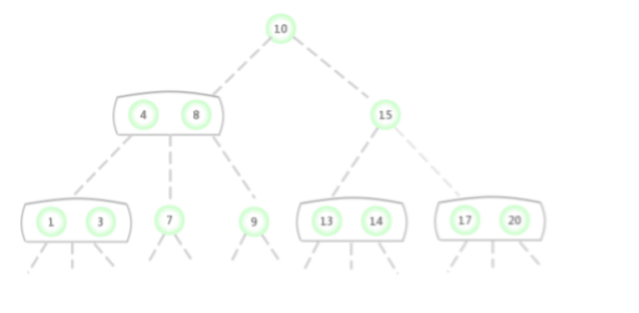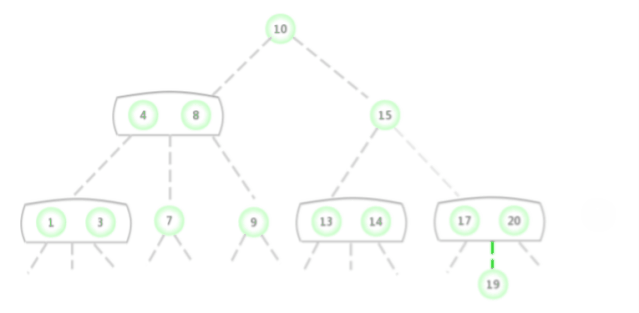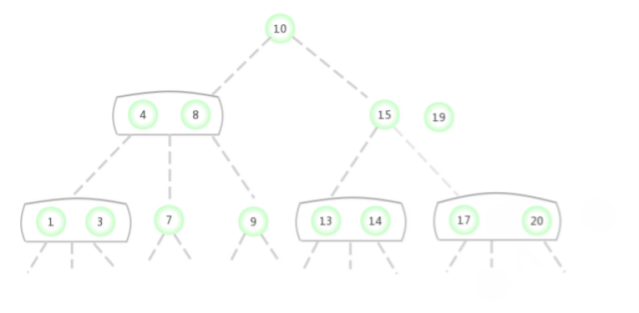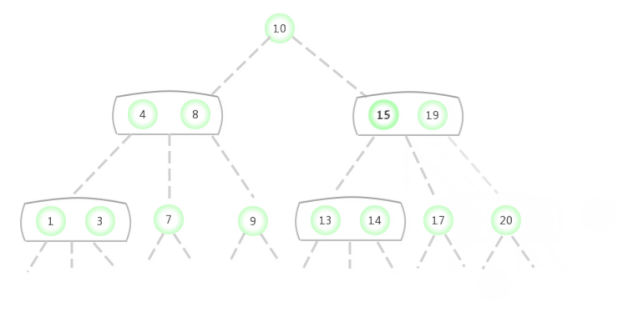
向一个父结点为3-结点的3-结点中插入新键
假设未命中查找结束于一个父结点为3-结点的3-结点。依旧需要构造一个临时的4-结点并分解它,然后将它的中键插入它的父结点中。由于父结点也是一个3-结点,插入中间后又形成一个新的临时4-结点,然后在这个节点上进行相同的变换,集分解这个父结点并将它的中键插入的它的父结点中去。推广到一般的情况,就是这样一直向上不断分解临时的4-结点并将中键插到更高层的父结点,直到遇到一个2-结点并将它替换为一个不需要继续分解的3-结点,或者是到达3-结点的根。
图示过程如下:
分解根结点
如果从插入节点到根结点的路径上都是3-结点,根结点最终变成一个临时的4-结点。此时可以按照向一棵只有一个*3-结点的树中插入新键的方法处理这个问题。将临时的4-结点分解为三个2-结点**,树高加1。这次最后的变化仍然保持了树的完美平衡性,因为它变换的是根结点。
图示过程如下:
4-结点的分解
在2-3树中4-结点出现的位置有如下的几种情况。
- 1.根结点
- 2.父结点为2-结点的左子结点或右子节点
- 3.父节点为3-节点的左子节点、中间的子结点或右子结点
下面我们来详细看一下在2-3树中出现上述的位置时如何分解。
情形:
当临时的4-节点出现在根节点:
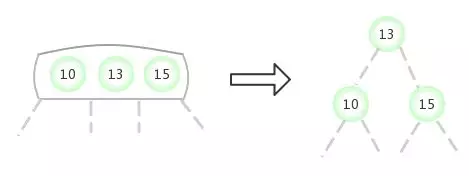
当临时的4-节点出现在2-结点的左侧:
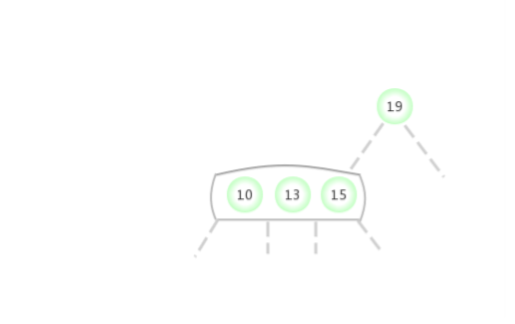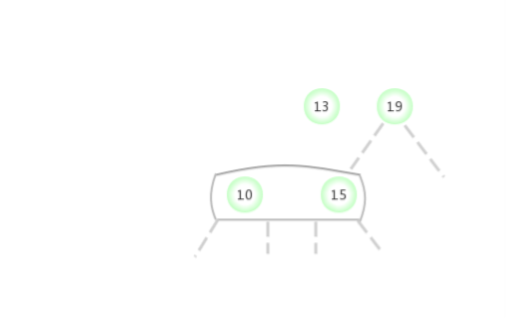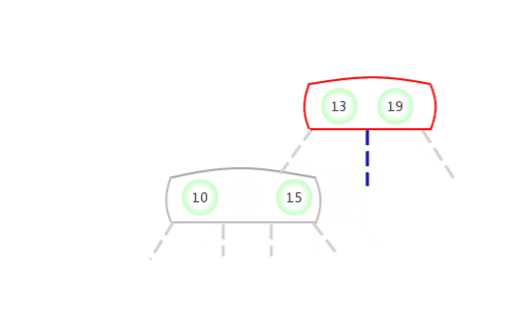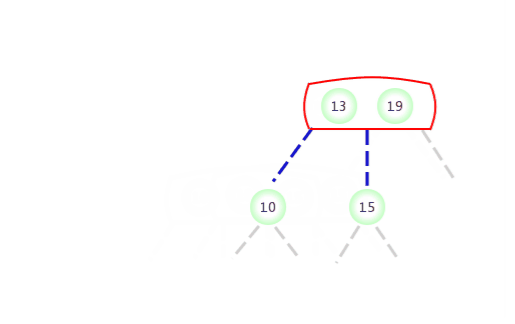
当临时的4-节点出现在2-结点的右侧:
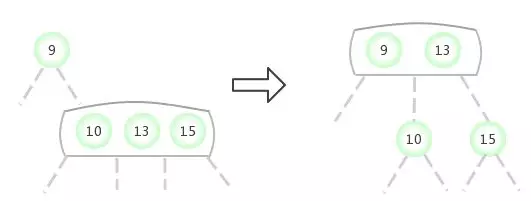
当临时的4-节点出现在3-结点的左侧:
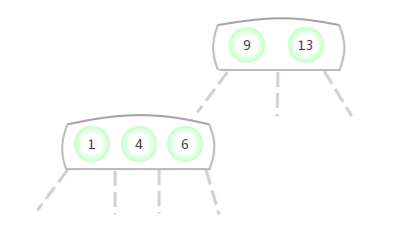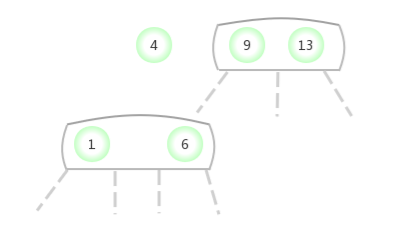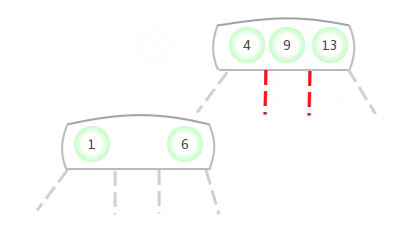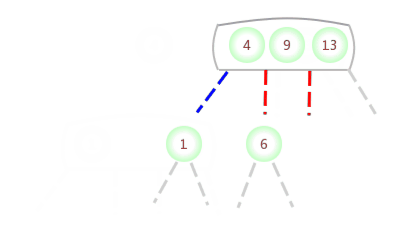
当临时的4-节点出现在3-结点的中间:
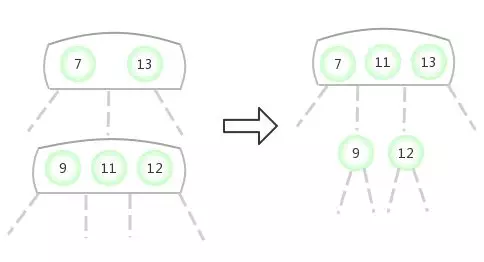
当临时的4-节点出现在3-结点的右侧:
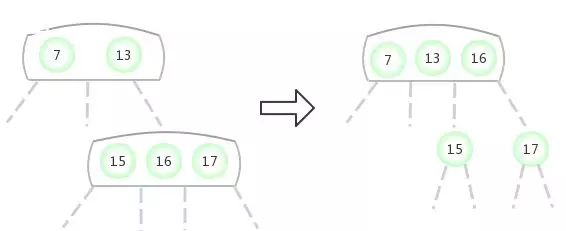
上述的情况中,在变化的过程中,只有当根节点最后为临时的4-节点,此时被分解成为3个2-结点时,整个树的高度才会增加1。除此之外,插入一个结点2-3树的高度还是原来的高度。上述的变化过程中:任何空链接到根节点的路径长度都是相等的。
结论
在一棵大小为N的2-3树中,查找和插入的操作访问的结点必然不会超过lgN。
- 证明:一棵含有N个结点的2-3树的高度在在log2 N和log3 N之间。
边栏推荐
- Low success rate of unit test report
- Unityhub cracking & unity cracking
- 漏洞复现-Fastjson 反序列化
- 一种适用于应用频繁测试下快速查看Pod的日志的方法(grep awk xargs kuberctl)
- Leetcode medium question my schedule I
- 面试题(CAS)
- Lua programming learning notes
- Analysis of maker education in innovative education system
- The largest 3 same digits in the string of leetcode simple question
- rsync远程同步
猜你喜欢
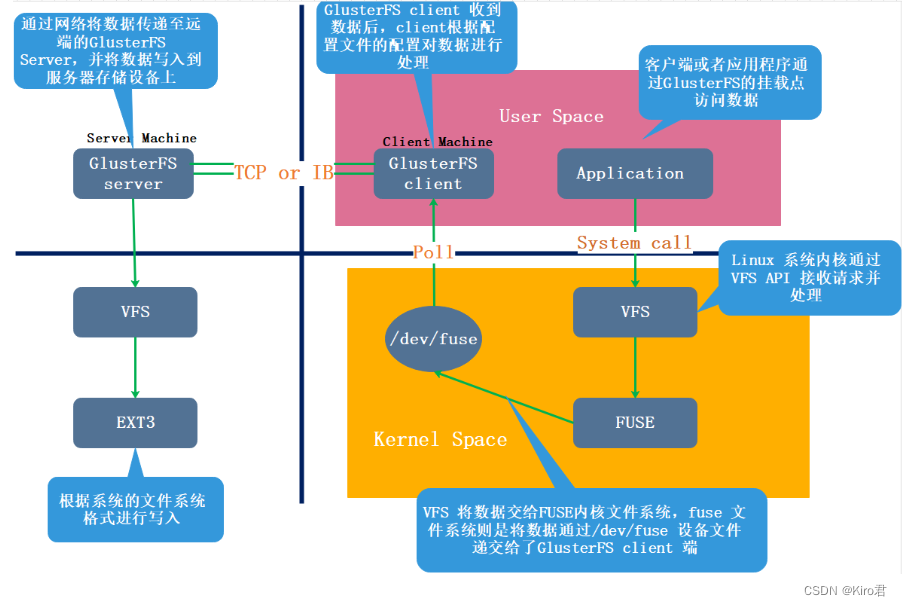
GFS distributed file system

Analysis of maker education in innovative education system
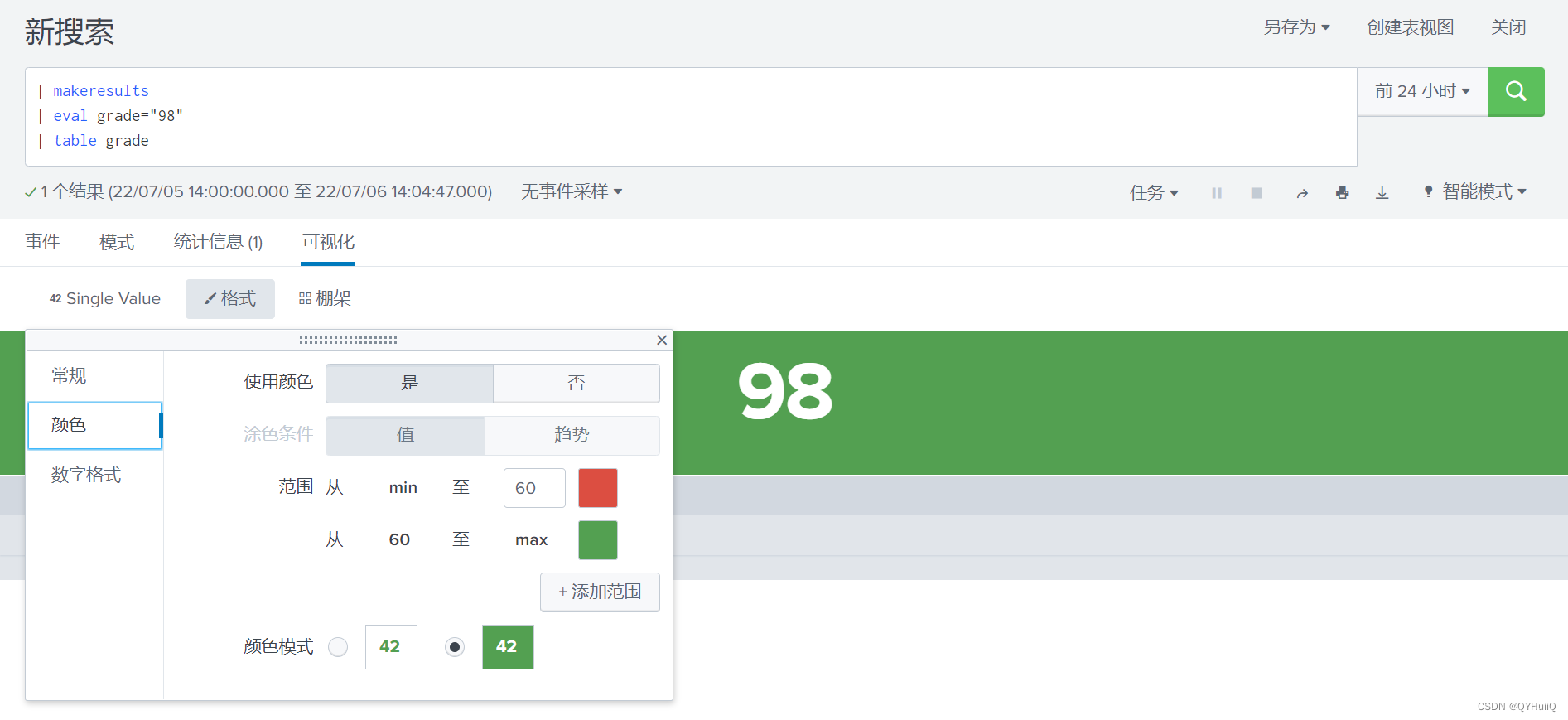
Splunk中single value视图使用将数值替换为文字

漏洞复现-easy_tornado
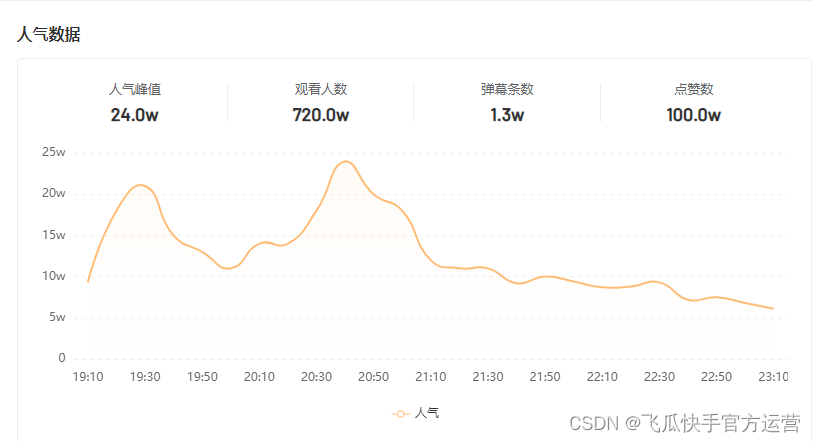
单场带货涨粉10万,农村主播竟将男装卖爆单?

Give full play to the wide practicality of maker education space
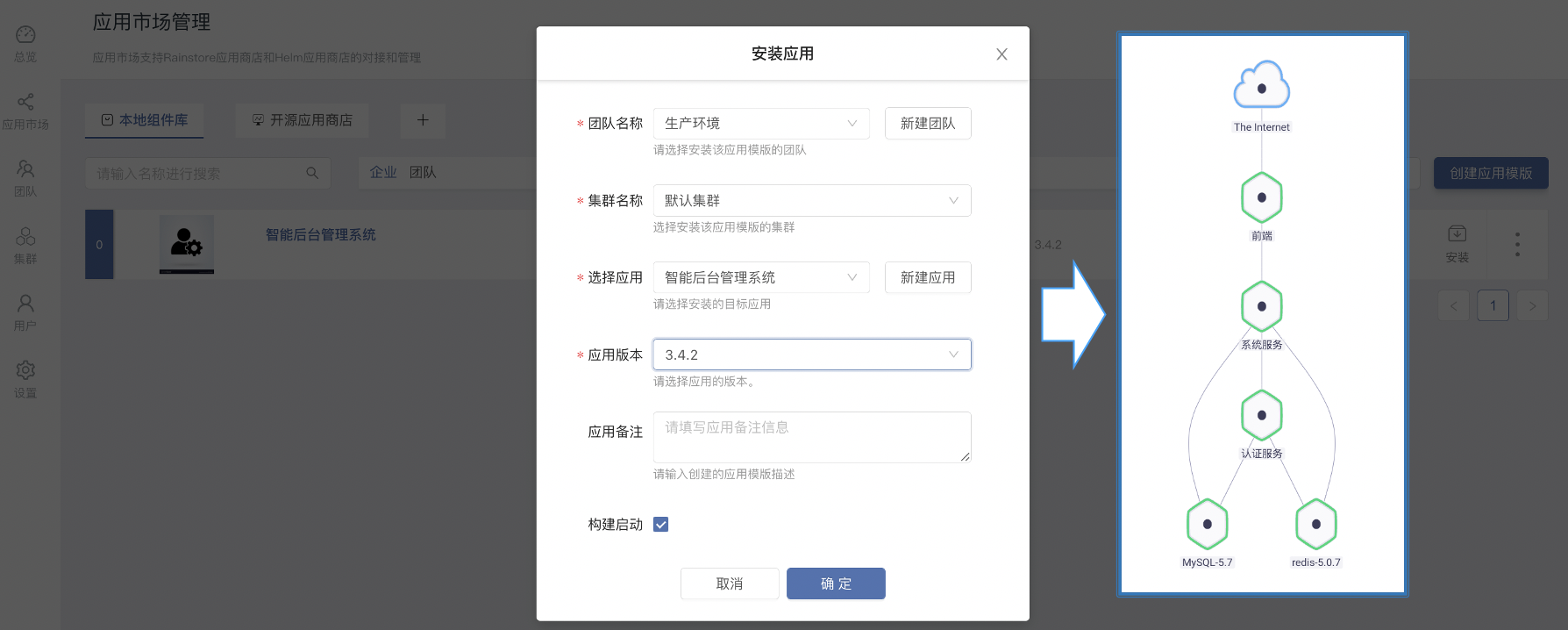
Improve the delivery efficiency of enterprise products (1) -- one click installation and upgrade of enterprise applications
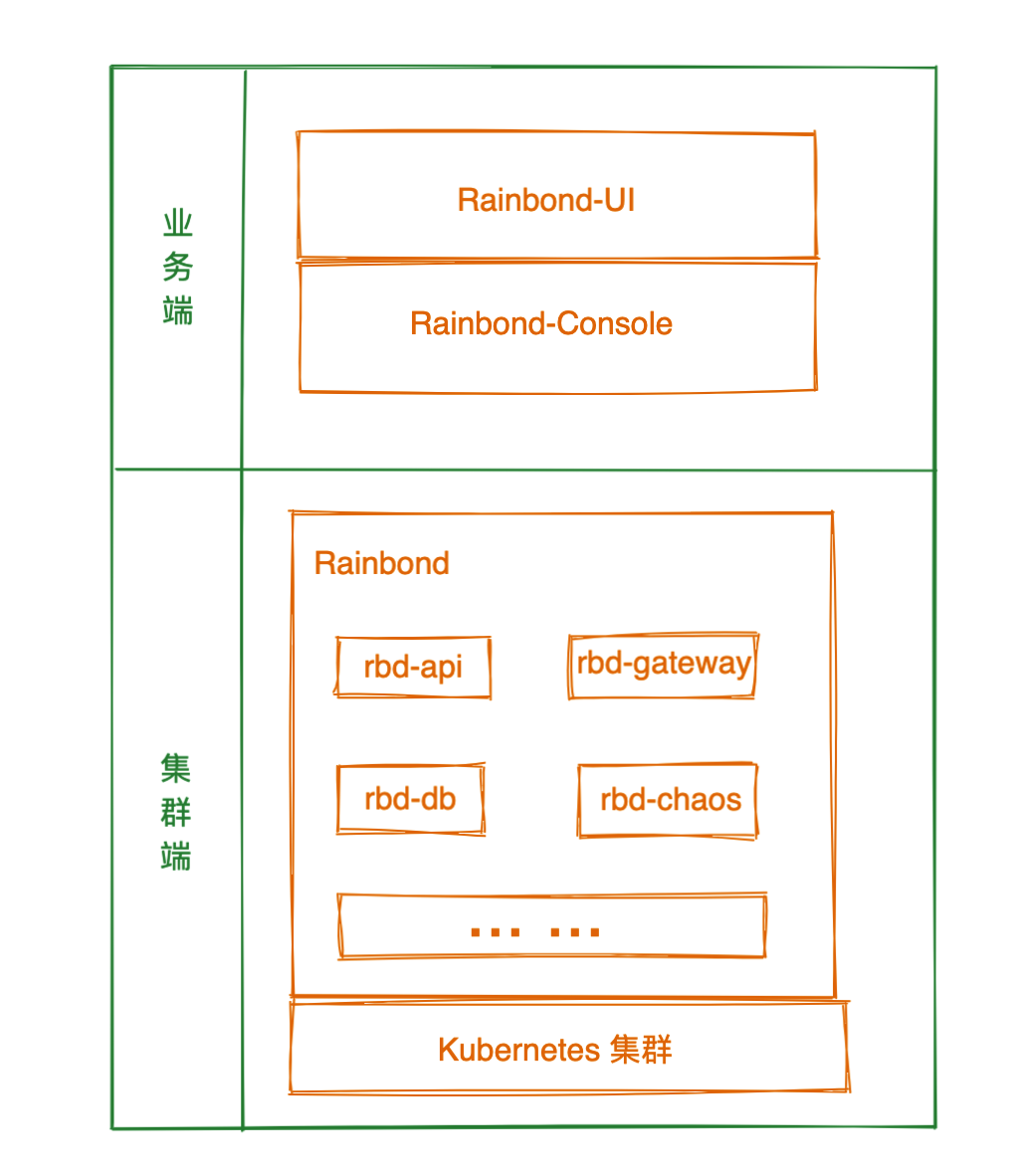
一文了解如何源码编译Rainbond基础组件

Leetcode medium question my schedule I

提高企业产品交付效率系列(1)—— 企业应用一键安装和升级
随机推荐
Detailed explanation of apply, also, let, run functions and principle analysis of internal source code in kotlin
buureservewp(2)
Interpreting the practical application of maker thinking and mathematics curriculum
Qinglong panel -- finishing usable scripts
Caractéristiques de bisenet
Coquette data completes the cloud native transformation through rainbow to realize offline continuous delivery to customers
Full text query classification
漏洞复现-easy_tornado
Lua programming learning notes
Offer harvester: add and sum two long string numbers (classic interview algorithm question)
The truth of robot education in hands-on practice
Register of assembly language by Wang Shuang
Game attack and defense world reverse
Kotlin combines flatmap for filtering and zip merge operators
Splunk子查询模糊匹配csv中字段值为*
Splunk中single value视图使用将数值替换为文字
BiSeNet的特點
轻松上手Fluentd,结合 Rainbond 插件市场,日志收集更快捷
Leetcode medium question my schedule I
Using helm to install rainbow in various kubernetes