Exotic curiosity-a solution looking - bit operations

位运算概览

符号	描述	运算规则	例子
&	与	两个位都为1时,结果才为1,否则结果为0	3&5=0011&0101=0001=1
	或	参加运算的两个对象只要有一个为1,其值为1.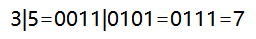
^	异或	两个位相同为0,相异为1	3^ 5=0011^0101=1001=9
~	取反	0变1,1变0
<<	左移	各二进位全部左移若干位,高位丢弃,低位补0	1010 1110<<2=1011 1000
>>	右移	各二进位全部右移若干位,对无符号数,高位补0,有符号数,各编译器处理方法不一样,有的补符号位（算术右移）,有的补0（逻辑右移）

注意：负数按补码形式参加按位与运算.

1.与运算符（&）

	与运算的用途
取一个数的指定位	比如取数 X=1010 1110 的低4位,只需要另找一个数Y,令Y的低4位为1,其余位为0,即Y=0000 1111,然后将X与Y进行按位与运算（X&Y=0000 1110）即可得到X的指定位.
清零	如果想将一个单元清零,即使其全部二进制位为0,只要与一个各位都为零的数值相与,结果为零.
判断奇偶	只要根据最未位是0还是1来决定,为0就是偶数,为1就是奇数.因此可以用if ((a&1)==0)代替if (a%2 == 0)来判断a是不是偶数.

2.或运算符（|）

	或运算的用途
常用来对一个数据的某些位设置为1	比如将数 X=1010 1110 的低4位设置为1,只需要另找一个数Y,令Y的低4位为1,其余位为0,即Y=0000 1111,然后将X与Y进行按位或运算（X

3.异或运算符（^）

异或的几条性质:
1、交换律
2、结合律 (a^ b)^ c == a^ (b^c)
3、对于任何数x,都有 x^x=0,x0=x
4、自反性: a^ b^ b=a^0=a;

	异或运算的用途
翻转指定位	比如将数 X=1010 1110 的低4位进行翻转,只需要另找一个数Y,令Y的低4位为1,其余位为0,即Y=0000 1111,然后将X与Y进行异或运算（X^Y=1010 0001）即可得到.
与0相异或值不变	例如：1010 1110 ^ 0000 0000 = 1010 1110
交换两个数	交换a与b的值,a ^= b;b ^= a; a ^= b;

void Swap(int& a, int& b)
{
    
	if (a != b)
	{
    
		a ^= b;
		b ^= a;
		a ^= b;
	}
}

4.取反运算符 (~)

	取反运算的用途
使一个数的最低位为零	使a的最低位为0,可以表示为：a &~ 1.~1的值为 1111 1111 1111 1110,再按"与"运算,最低位一定为0.因为“ ~”运算符的优先级比算术运算符、关系运算符、逻辑运算符和其他运算符都高.

5.左移运算符（<<）

定义：将一个运算对象的各二进制位全部左移若干位（左边的二进制位丢弃,右边补0）.
若左移时舍弃的高位不包含1,则每左移一位,相当于该数乘以2.

6.右移运算符（>>）

定义：将一个数的各二进制位全部右移若干位,正数左补0,负数左补1,右边丢弃.
例如：a=a>>2 将a的二进制位右移2位,左补0 或者 左补1得看被移数是正还是负.
操作数每右移一位,相当于该数除以2.

注意

不同长度的数据进行位运算：如果两个不同长度的数据进行位运算时,系统会将二者按右端对齐,然后进行位运算.
以“与运算”为例说明如下：我们知道在C语言中long型占4个字节,int型占2个字节,如果一个long型数据与一个int型数据进行“与运算“,右端对齐后,左边不足的位依下面三种情况补足：
1）如果整型数据为正数,左边补16个0.
2）如果整型数据为负数,左边补16个1.
3）如果整形数据为无符号数,左边也补16个0.