当前位置:网站首页>动态规划 之 打家劫舍
动态规划 之 打家劫舍
2022-07-05 23:06:00 【chenyfan_】
动态规划 之 打家劫舍
198. 打家劫舍 ●●
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
–
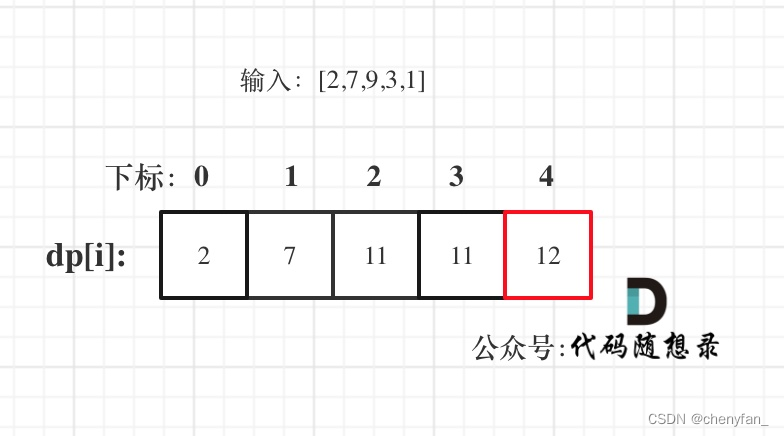
输入:[2,7,9,3,1]
输出:12
解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。 偷窃到的最高金额 = 2 + 9 + 1 = 12 。
- 动态规划,二维数组,偷或不偷 nums[i] 表示为 dp[i][1] 和 dp[i][0]
class Solution {
public:
int rob(vector<int>& nums) {
int n = nums.size();
vector<vector<int>> dp(n, vector<int>(2, 0));
dp[0][1] = nums[0];
for(int i = 1; i < n; ++i){
dp[i][0] = max(dp[i-1][0], dp[i-1][1]); // 不偷nums[i]
dp[i][1] = dp[i-1][0] + nums[i]; // 偷nums[i]
}
return max(dp[n-1][0], dp[n-1][1]);
}
};
- 动态规划,一维数组
- dp[j]:考虑下标 j(包括j)以内的房屋,最多可以偷窃的金额为dp[j]。
dp[j] = max(dp[j-1], dp[j-2] + nums[j]);
考虑偷或不偷下标 j- dp[0] = nums[0];
dp[1] = max(nums[0], nums[1]); - 从前往后遍历
class Solution {
public:
int rob(vector<int>& nums) {
int n = nums.size();
if (n == 0) return 0;
if (n == 1) return nums[0];
vector<int> dp(n, 0); // dp[j]
dp[0] = nums[0];
dp[1] = max(nums[0], nums[1]); // 0 和 1 只能偷一个
for(int j = 2; j < n; ++j){
// 偷 或 不偷 nums[j]
dp[j] = max(dp[j-1], dp[j-2] + nums[j]);
}
return dp[n-1];
}
};
213. 打家劫舍 II ●●
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
本题中房屋首尾连接成环了,因此,将房屋分为两种情况,转化为两个不成环的打家劫舍问题单独计算:
- 考虑(但不一定取)第一个房屋,不考虑最后一个房屋;
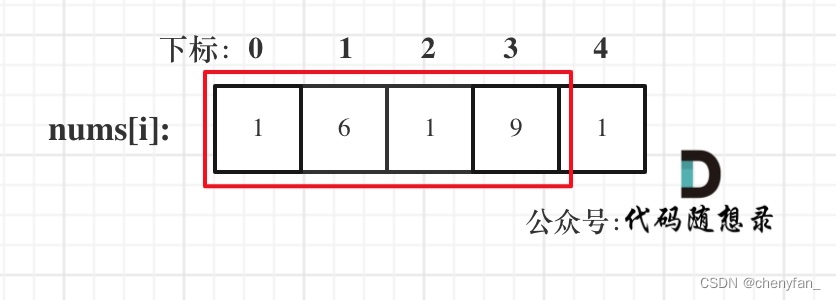
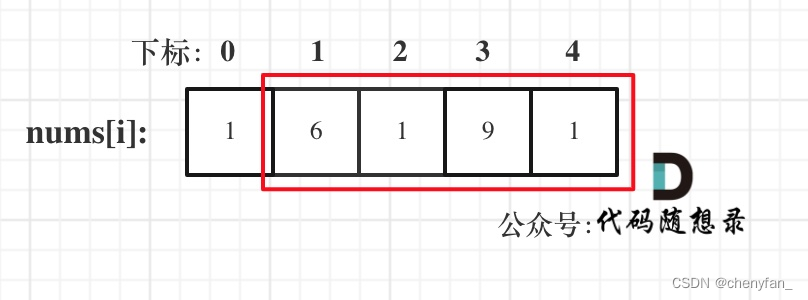
- 考虑(但不一定取)最后一个房屋,不考虑第一个房屋。
class Solution {
public:
int subRob(vector<int>& nums, int strat, int end){
int n = end - strat + 1; // 子集个数
if(n == 1) return nums[strat];
vector<int> dp(n, 0);
dp[0] = nums[strat];
dp[1] = max(nums[strat], nums[strat + 1]);
for(int j = 2; j < n; ++j){
dp[j] = max(dp[j-1], dp[j-2] + nums[j+strat]);
}
return dp[n-1];
}
int rob(vector<int>& nums) {
int n = nums.size();
if(n == 1) return nums[0];
int strat = subRob(nums, 0, n-2); // [0, n-2]
int end = subRob(nums, 1, n-1); // [1, n-1]
return max(strat, end);
}
};
337. 打家劫舍 III ●●
小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为 root 。
除了 root 之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ,房屋将自动报警。
给定二叉树的 root 。返回 在不触动警报的情况下 ,小偷能够盗取的最高金额 。
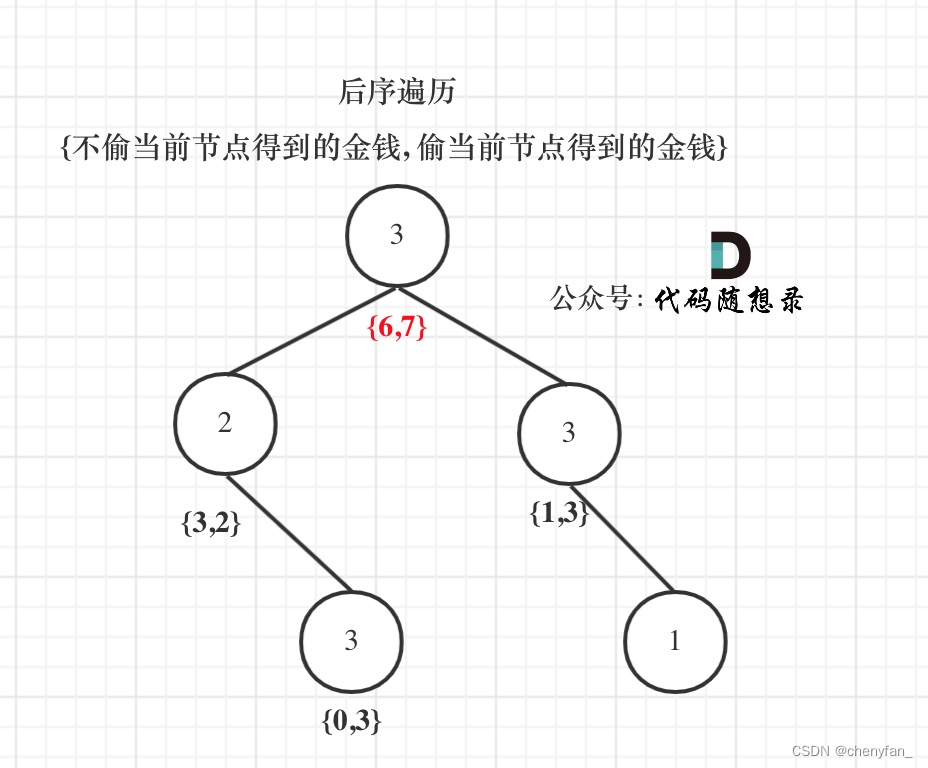
后序遍历,通过递归函数的返回值来做下一步计算。
如果偷了当前节点,两个孩子就不能动,并递归到孙子节点;
如果不偷当前节点,就可以考虑偷左右孩子(注意这里说的是“考虑”)
1. 记忆化递归搜索
避免节点的重复计算,用哈希表存储计算过的节点金额。
- 时间复杂度: O ( n ) O(n) O(n)
- 空间复杂度: O ( log n ) O(\log n) O(logn),算上递推系统栈的空间
class Solution {
public:
unordered_map<TreeNode*, int> map;
int rob(TreeNode* root) {
if(root == nullptr) return 0;
if(root->left == nullptr && root->right == nullptr) return root->val; // 叶子节点,直接返回值
if(map[root]) return map[root]; // 记忆化搜索哈希
// 偷父节点,递归遍历孙子节点
int val1 = root->val;
if(root->left != nullptr) val1 += rob(root->left->left) + rob(root->left->right);
if(root->right != nullptr) val1 += rob(root->right->left) + rob(root->right->right);
// 不偷父节点,递归遍历孩子节点
int val2 = rob(root->left) + rob(root->right);
// 取最大值,并存储记忆
map[root] = max(val1, val2);
return map[root];
}
};
2. 动态规划(树形dp)
以上记忆化搜索对一个节点 偷与不偷 得到的最大金钱都没有做记录,而是需要实时计算比较。
而动态规划其实就是使用状态转移容器数组dp[]来记录状态的变化,dp[0] 表示不偷该节点得到的最大金额,dp[1]表示偷该节点得到的最大金额。
- 时间复杂度: O ( n ) O(n) O(n),每个节点只遍历了一次
- 空间复杂度: O ( log n ) O(\log n) O(logn),算上递推系统栈的空间
class Solution {
public:
vector<int> robTree(TreeNode* root) {
if(root == nullptr) return {
0, 0};
vector<int> dp(2, 0);
// 考虑孩子节点
vector<int> left = robTree(root->left);
vector<int> right = robTree(root->right);
// 不偷该节点,下标为0,孩子节点可偷可不偷
dp[0] = max(left[0], left[1]) + max(right[0], right[1]);
// 偷该节点,下标为1,不能偷孩子节点
dp[1] = root->val + left[0] + right[0];
return dp;
}
int rob(TreeNode* root) {
vector<int> ans = robTree(root);
return max(ans[0], ans[1]);
}
};
边栏推荐
- ORB_ SLAM2/3
- Non rigid / flexible point cloud ICP registration
- What is the process of building a website
- 【Note17】PECI(Platform Environment Control Interface)
- Multi view 3D reconstruction
- 2.13 summary
- C# Linq Demo
- The maximum happiness of the party
- 视频标准二三事
- Development specification: interface unified return value format [resend]
猜你喜欢

数学公式截图识别神器Mathpix无限使用教程

There are 14 God note taking methods. Just choose one move to improve your learning and work efficiency by 100 times!

CJ mccullem autograph: to dear Portland
LabVIEW打开PNG 图像正常而 Photoshop打开得到全黑的图像
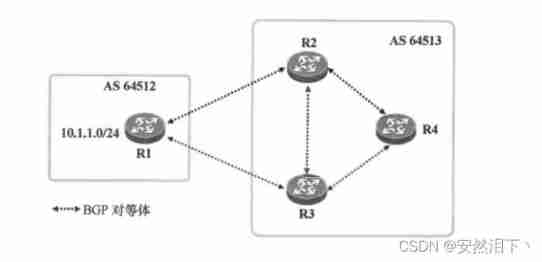
Hcip day 12 (BGP black hole, anti ring, configuration)
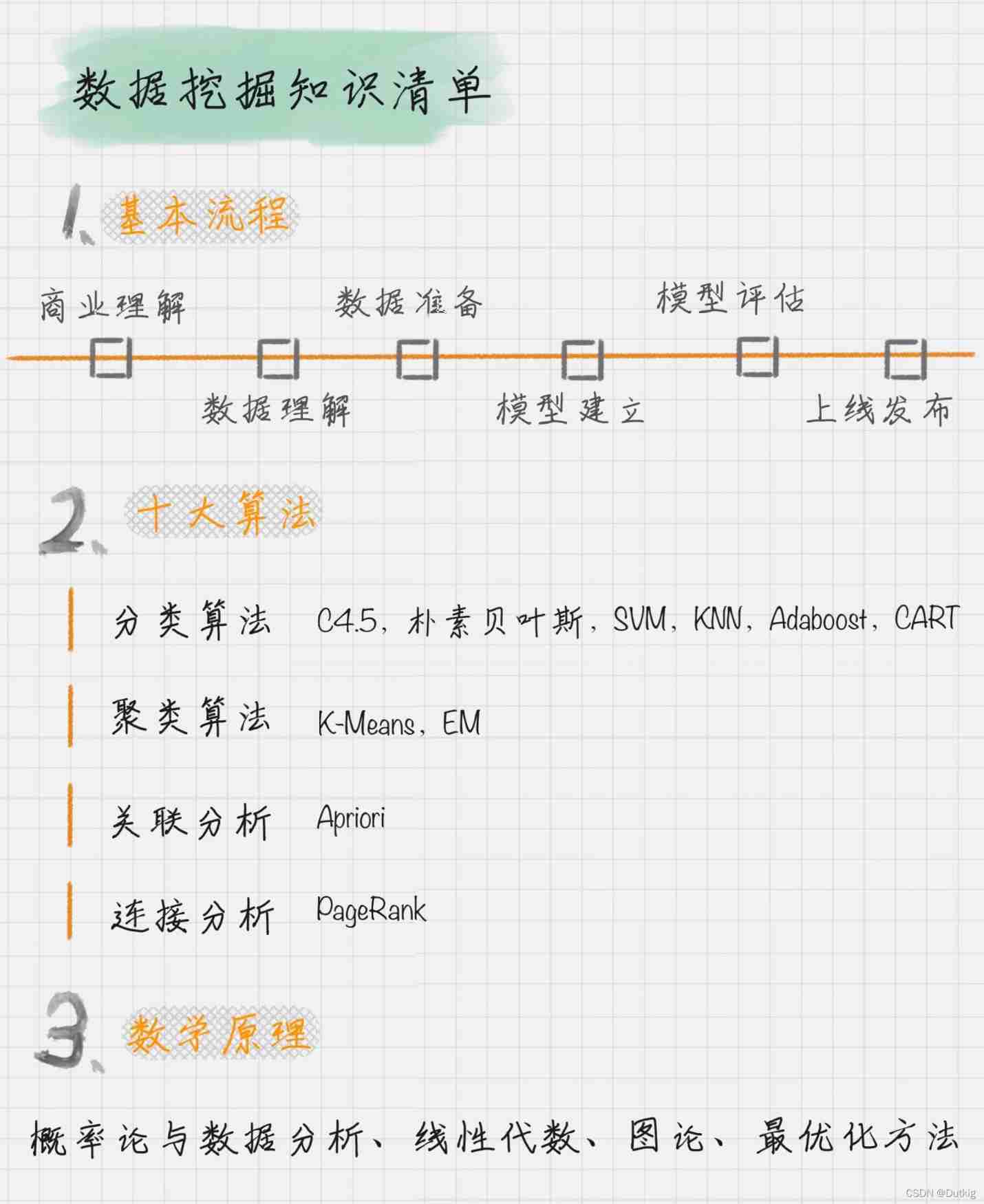
Data analysis - Thinking foreshadowing
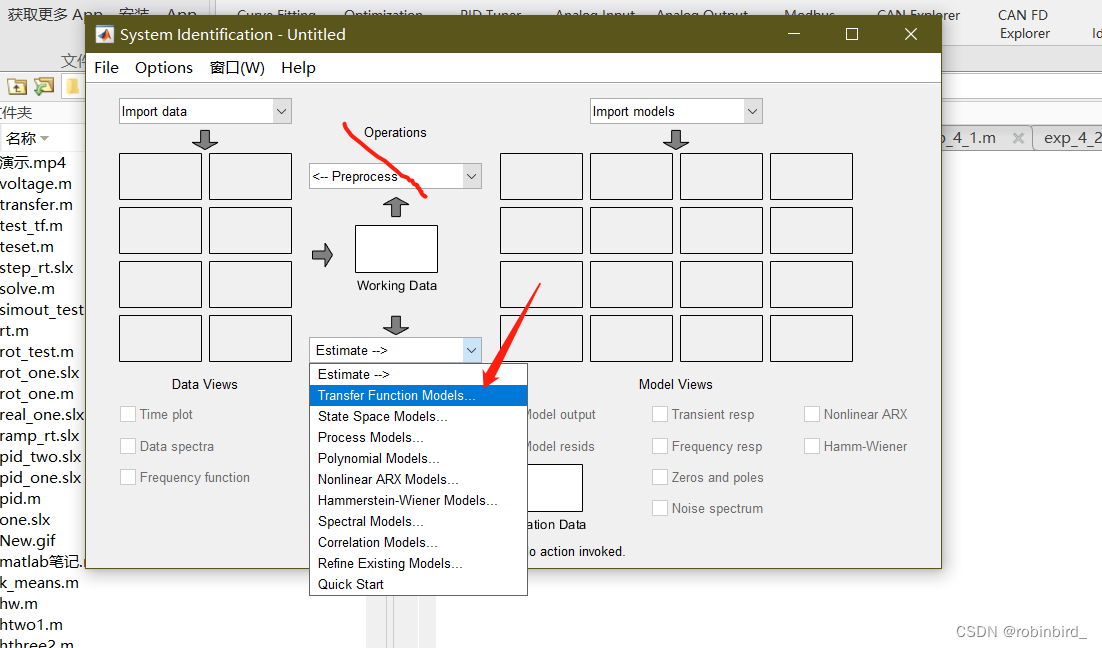
【经典控制理论】自控实验总结
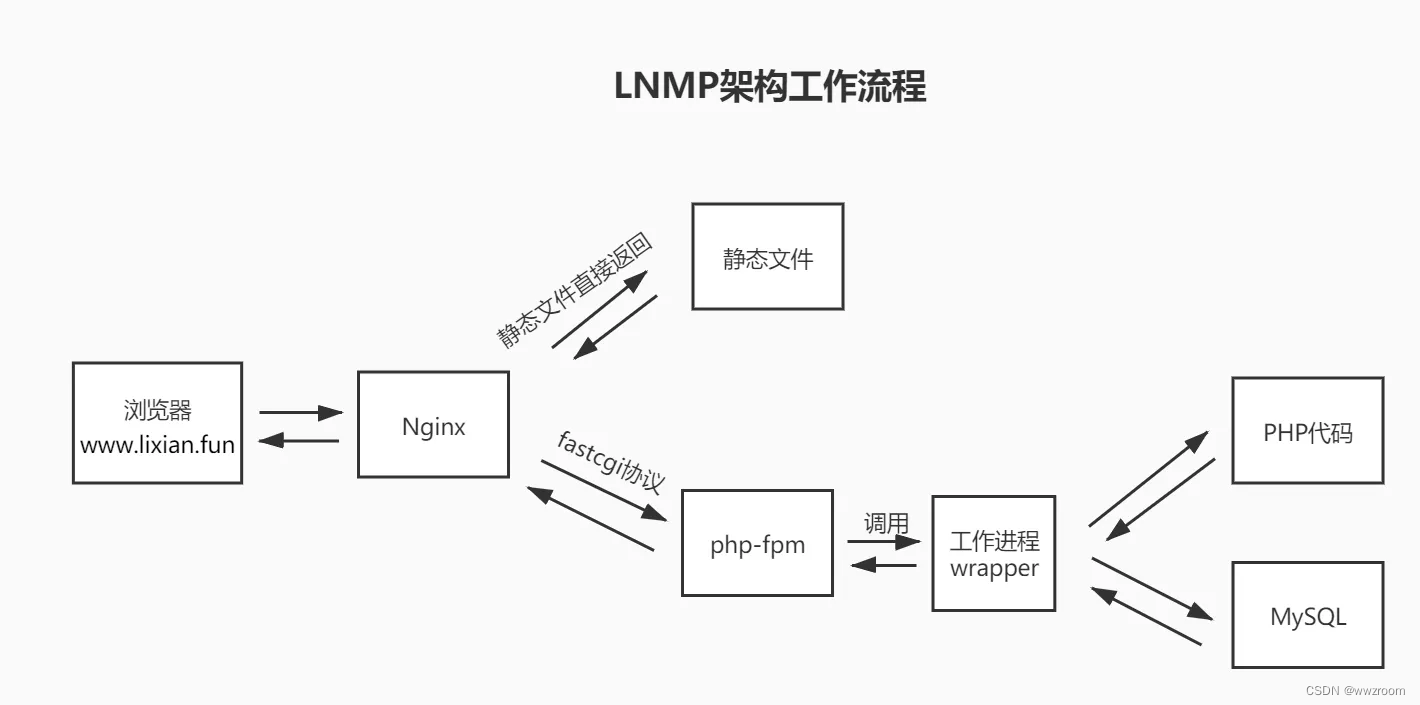
第十七周作业
Matlab smooth curve connection scatter diagram
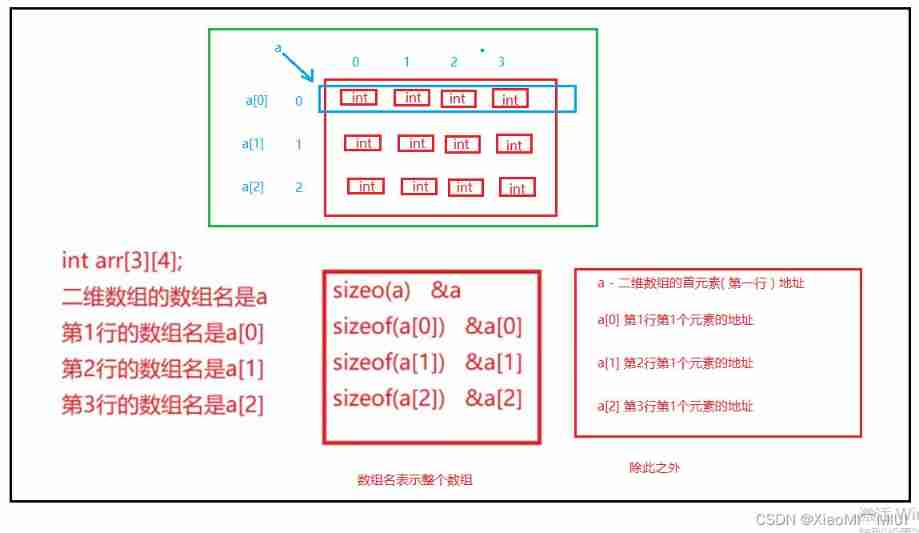
Detailed explanation of pointer and array written test of C language
随机推荐
Non rigid / flexible point cloud ICP registration
Use of metadata in golang grpc
Composition of interface
C# Linq Demo
Krypton Factor-紫书第七章暴力求解
[untitled]
Go language implementation principle -- lock implementation principle
(4) UART application design and simulation verification 2 - RX module design (stateless machine)
C Primer Plus Chapter 9 question 9 POW function
Multi sensor fusion of imu/ electronic compass / wheel encoder (Kalman filter)
Southeast Asia e-commerce guide, how do sellers layout the Southeast Asia market?
Douban scoring applet Part-2
Idea rundashboard window configuration
Commonly used probability distributions: Bernoulli distribution, binomial distribution, polynomial distribution, Gaussian distribution, exponential distribution, Laplace distribution and Dirac delta d
Registration of Electrical Engineering (elementary) examination in 2022 and the latest analysis of Electrical Engineering (elementary)
并查集实践
Solution to the packaging problem of asyncsocket long connecting rod
Neural structured learning - Part 2: training with natural graphs
(4)UART應用設計及仿真驗證2 —— TX模塊設計(無狀態機)
UART Application Design and Simulation Verification 2 - TX Module Design (Stateless machine)